L204

4

ЛАБОРАТОРНАЯ РАБОТА N 204

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ СИЛЫ ТОКА, НАПРЯЖЕНИЯ, МОЩНОСТИ И КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ ЦЕПИ ПОСТОЯННОГО ТОКА ОТ СОПРОТИВЛЕНИЯ НАГРУЗКИ ЗАМКНУТОЙ ЦЕПИ

ПРИБОРЫ И ОБОРУДОВАНИЕ: блок питания, сменный модуль, измерительные приборы, магазин сопротивления

I. ТЕОРИЯ МЕТОДА

З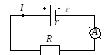амкнутой называется цепь, состоящая из источника постоянного тока и сопротивления нагрузки.

Рис. 1

На рис. 1 представлена замкнутая цепь, где - источник тока с внутренним сопротивлением ; R – сопротивление нагрузки (внешний участок цепи); А – амперметр, прибор для определения силы тока.

Сила тока определяется по закону Ома для замкнутой цепи

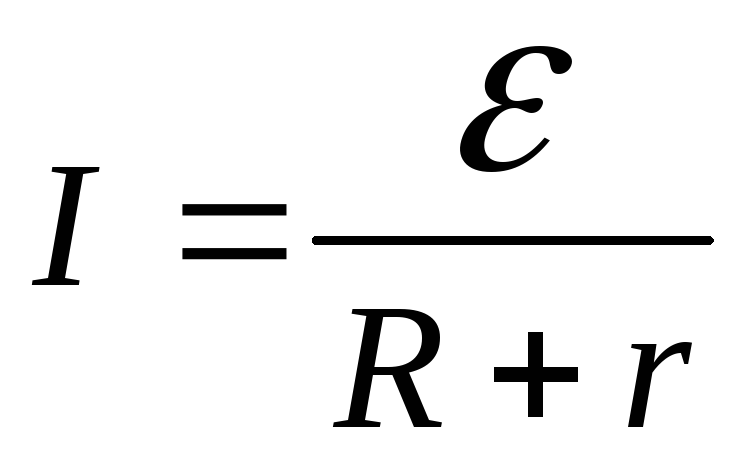, (1)

где - Э.Д.С. источника тока;

(R+r) – полное сопротивление цепи.

Исследуем зависимость силы тока от сопротивления нагрузки R. По формуле (1) вычислим силу тока при следующих значениях сопротивления нагрузки R=0 (короткое замыкание), R=r (внешнее сопротивление равно внутреннему) и R (цепь разомкнута). Соответственно получаем: (максимальное значение тока); и .

Представим полученную зависимость графически (рис.2).

Сила тока связана с сопротивлением нагрузки (внешним сопротивлением цепи) обратной зависимостью. Сила тока убывает с ростом сопротивления.

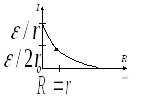
Рис. 2

Преобразуем выражение (1) относительно Э.Д.С.

, (2)

где - напряжение на сопротивлении нагрузки (внешний участок цепи);

- напряжение на источнике (внутренний участок цепи).

Таким образом, согласно (2), Э.Д.С. источника тока численно равна сумме падений напряжений на внешнем и внутреннем участках цепи.

Исследуем зависимость падения напряжения на внешнем участке от сопротивления нагрузки .

Преобразуем формулу , подставив в нее (1)

. (3)

В

ычисляем при , получаем соответственно , и (рис.3).

0

R



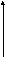
Рис. 3

Напряжение растет с ростом сопротивления нагрузки и в пределе стремится к Э.Д.С. ().

Преобразуем формулу (2), умножив обе ее части на силу тока .

, (4)

где - полная мощность источника тока;

- полезная мощность цепи;

- потери мощности внутри источника тока.

Полученная формула (4) - закон сохранения мощности замкнутой цепи. Исследуем зависимость полезной мощности Р₁ от сопротивления нагрузки R.

Полезная мощность

(5)

при и ( и ) равна нулю, остальные ее значения больше нуля,

так как ни , ни не могут быть отрицательными.

Все значения и лежат выше оси сопротивлений, поэтому график зависимости должен иметь точку экстремума, удовлетворяющую условию . Преобразуем формулу (5) подставив в нее выражение (1). Полученную формулу

(6)

продифференцируем по R,

.

Полезная мощность имеет экстремум при , то есть когда внешнее сопротивление равно внутреннему . На рис. 4 кривая 1 - график зависимости полезной мощности от сопротивления нагрузки . На участке кривой полезная мощность возрастает, в точке она максимальна и равна , а на участке - убывает.

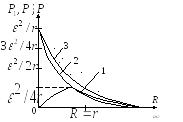
Рис. 4

Кривая 2 на рис. 4 - график зависимости потерь мощности от cсопротивления нагрузки . Потери мощности вычисляют по формуле и (при ) принимают значения ; и .

С ростом сопротивления нагрузки потери мощности убывают, при обращаются в 0.

Кривая 3 на рис. 4 - график зависимости полной мощности от сопротивления нагрузки .

Полная мощность вычисляется по формуле . Она максимальна и равна при , и минимальна при . Полная мощность убывает с ростом сопротивления нагрузки.

Для характеристики машин, механизмов, электрических цепей применяется коэффициент полезного действия , измеряемый отношением полезной мощности к полной .

. (7)

Преобразуем формулу (7), подставляя в нее и , и учитывая, что получаем

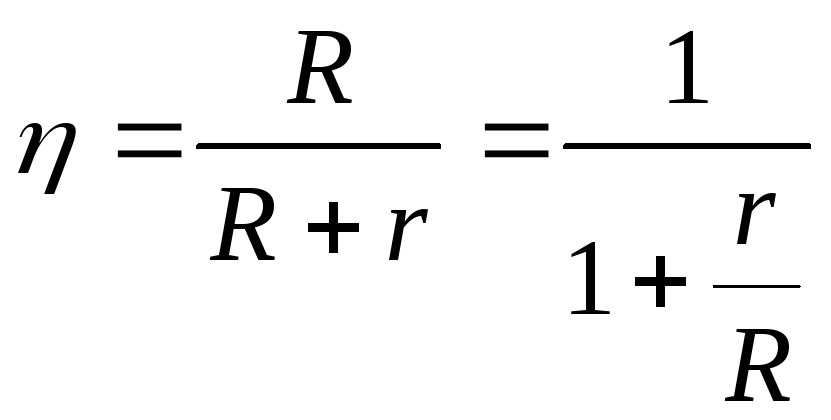
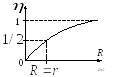. (8)

Рис. 5

Согласно формуле (8) при сопротивлении нагрузки получаем следующие значения коэффициента полезного действия ; 1/2; 1 (рис.5). Коэффициент полезного действия растет с ростом внешнего сопротивления, при к.п.д. .

В данной работе экспериментально исследуются рассмотренные зависимости.

2. ЗАДАНИЕ

2.1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Какая цепь называется замкнутой? Сформулируйте закон Ома для замкнутой цепи, поясните все величины в него входящие. Представьте графически зависимость силы тока от сопротивления нагрузки .

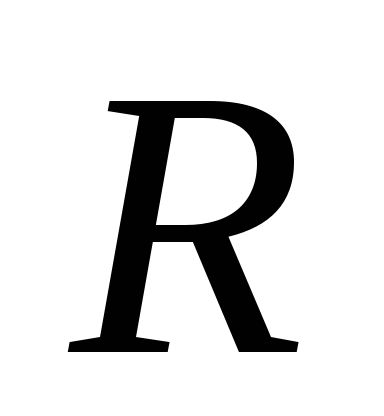2. Что такое напряжение? Какие напряжения различают в замкнутой цепи? Выведите формулу зависимости напряжения на внешнем участке цепи от сопротивления этого участка (представьте графически эту зависимость).

3. Запишите закон сохранения мощности для замкнутой цепи. Поясните все величины в этом законе. Получите формулы зависимости полезной мощности, потерь мощности и полной мощности от сопротивления нагрузки, представьте эти зависимости графически. Поясните, при каком условии полезная мощность максимальна.

4. Каким отношением измеряется к.п.д. замкнутой цепи? Выведите формулу, связывающую к.п.д. с сопротивлением нагрузки, представьте полученную зависимость графически.

2.2. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Сменный модуль соедините с помощью разъемов с блоком питания, что приведет к образованию цепи, изображенной на рис.1.

2. Изменяя сопротивление нагрузки от до (по указанию преподавателя), снимите зависимость силы тока 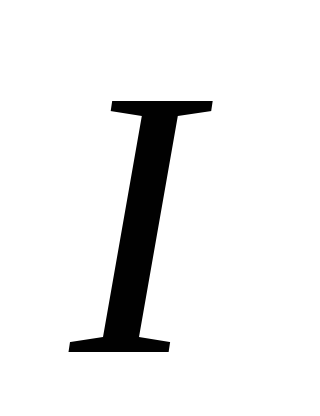от сопротивления 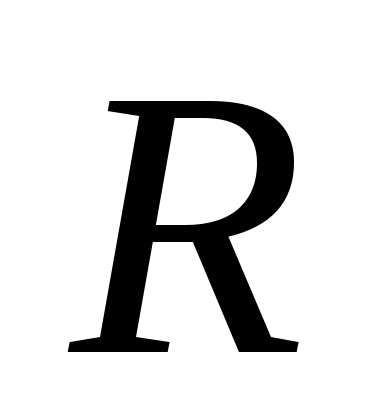. Результаты занесите в таблицу 1.

3. По полученным значениям и 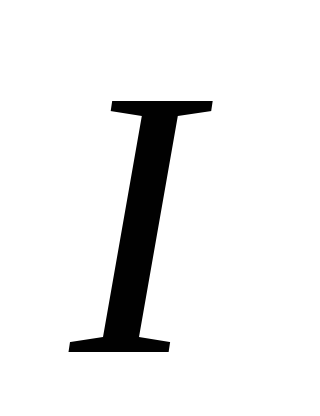вычислите (с помощью ЭВМ) напряжение 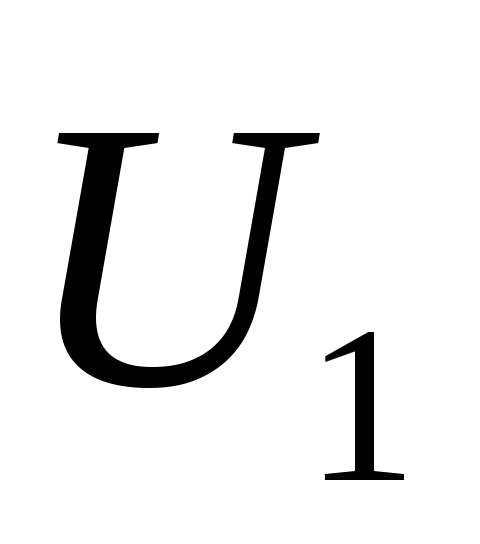, мощност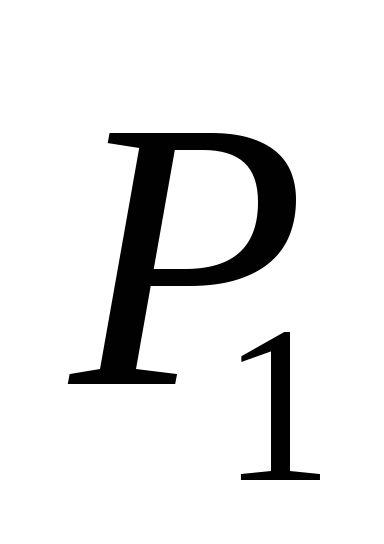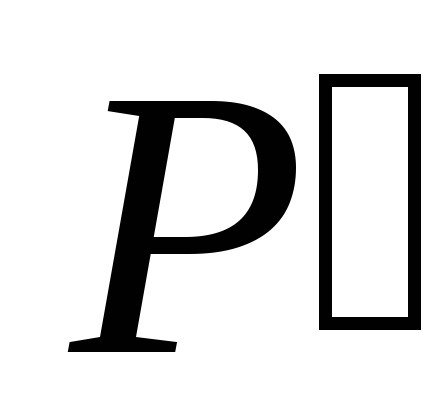и , и 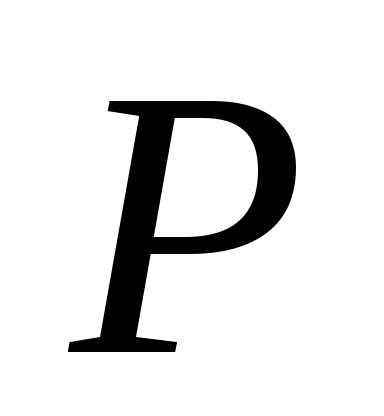и коэффициент полезного действия 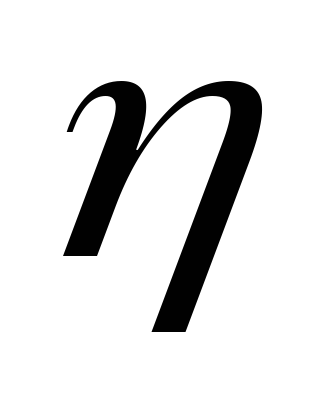, а также Э.Д.С. и внутреннее сопротивление источника тока.

4. Представьте полученные зависимости графически.

5. Сравните вид полученных экспериментальных кривых с видом соответствующих им теоретических кривых (рис. 2, 3, 4, 5). Оцените достоверность полученных экспериментальных результатов.

Таблица 1

№ п/п	, Ом	, мА	, В	, Вт	, Вт	, Вт	, %
1 2 