
- •«Челябинский государственный агроинженерный
- •Университет»
- •Гидравлика
- •Челябинск
- •Введение
- •Раздел 1 Гидравлика
- •Силы, действующие в жидкости
- •2. Физические свойства жидкости
- •2.1. Плотность и удельный вес жидкости
- •2.2. Сжимаемость жидкости
- •2.3. Температурное расширение жидкости
- •2.4. Вязкость жидкостей
- •3. Гидростатика
- •3.1. Свойства гидростатического давления
- •3.2. Дифференциальные уравнения равновесия жидкости (уравнения Леонарда Эйлера)
- •3.3. Основное уравнение гидростатики. Эпюры гидростатического давления
- •3.4. Сила гидростатического давления на плоские поверхности
- •3.5. Сила гидростатического давления, действующая на криволинейные поверхности
- •3.6. Закон Архимеда. Основы теории плавания
- •3.7. Гидростатические машины и механизмы
- •4. Гидродинамика
- •4.1. Основные понятия
- •4.2. Уравнение неразрывности (сплошности)
- •4.3. Уравнение д.Бернулли для элементарной струйки идеальной жидкости. График уравнения д.Бернулли
- •4.4. Уравнение д.Бернулли для элементарной струйки реальной жидкости. График уравнения д.Бернулли
- •4.5. Уравнение д.Бернулли для потока реальной жидкости
- •5. Определение гидравлических потерь
- •5.1. Классификация потерь напора
- •5.2. Основное уравнение равномерного движения
- •5.3. Формулы для определения гидравлических потерь
- •5.4. Режимы движения жидкости. Критерий рейнольдса
- •5.5. Особенности ламинарного режима движения жидкости
- •5.6. Особенности турбулентного режима движения жидкости
- •5.7. Влияние режима движения жидкости и шероховатости на величину коэффициента трения в трубах (график Никурадзе)
- •6. Гидравлический расчет трубопроводов
- •6.1. Классификация трубопроводов
- •6.2. Расходная характеристика трубопровода (модуль расхода)
- •6.3. Гидравлические характеристики трубопроводов
- •6.4. Равномерный путевой расход
- •6.5. Гидравлический удар в трубопроводах. Гидравлический таран
- •7. Истечение жидкости из отверстий и насадков
- •7.1. Истечение жидкости из малого отверстия в тонкой стенке
- •7.2. Истечение жидкости через насадки
- •8. Гидравлическое моделирование
- •8.1. Сущность моделирования
- •8.2. Основные законы гидродинамического подобия. Критерий подобия Ньютона
- •8.3. Критерий подобия Рейнольдса, Фруда, Эйлера, Вебера
- •Раздел 2 Гидравлические машины
- •9. Насосы
- •9.1. Классификация насосов
- •9.2. Основные параметры насосов
- •9.2.1. Напор, развиваемый насосом
- •9.2.2. Мощность и кпд насоса
- •9.3. Область применения насосов
- •10. Динамические насосы
- •10.1. Центробежные насосы
- •10.1.1. Схема устройства и принцип действия
- •10.1.2. Основное уравнение центробежного насоса
- •10.1.3. Подача центробежного насоса
- •10.1.4. Теоретические характеристики центробежного насоса
- •10.1.5. Действительная характеристика центробежного наоса
- •10.1.6. Универсальные характеристики центробежного насоса
- •10.1.7. Процесс всасывания и явление кавитации в центробежном насосе
- •10.1.8. Законы пропорциональности центробежного насоса
- •10.1.9. Работа центробежного насоса на сеть
- •10.1.10. Регулирование работы центробежного насоса
- •10.1.11. Совместная работа центробежных насосов
- •10.1.12. Центробежные насосы специального назначения
- •10.2. Насосы трения
- •10.2.1. Вихревые насосы
- •10.2.2. Струйные насосы
- •10.2.3. Воздушные насосы
- •10.2.4. Шнековые насосы
- •10.2.5. Дисковые насосы
- •10.2.6. Лабиринтные насосы
- •10.2.7. Вибрационные насосы
- •11. Объемные насосы
- •11.1. Возвратно - поступательные насосы
- •11.2. Роторные насосы
- •Раздел 3 гидравлическиЙ привод
- •12. Классификация
- •13. Объемный гидропривод
- •13.1. Функциональная схема
- •13.2. Принципиальная схема гидропривода
- •13.3. Область применения объемных гидроприводов
- •13.4. Достоинства и недостатки объемных гидроприводов
- •13.5. Требования к рабочей жидкости
- •13.6. Объемный гидропривод возвратно-поступательного движения
- •13.7. Принцип расчета гидропривода
- •13.8. Объемный гидропривод вращательного движения
- •13.9. Регулирование скорости гидропривода
- •13.9.1. Объемное регулирование
- •13.9.2. Дроссельное регулирование
- •13.10. Следящий гидропривод
- •14. Гидролинии, гидроемкости, фильтры
- •Раздел 4 сельскохозяйственное водоснабжение
- •15. Системы водоснабжения. Классификация.
- •Слово о воде
- •16. Водоснабжение из поверхностных источников
- •17. Водоснабжение из подземных источников
- •18. Водонапорные и регулирующие устройства
- •19. Требования, предъявляемые к качеству хозяйственно–питьевой воды. Методы улучшения качества воды
- •20. Основные данные для проектирования водопроводной сети
- •Раздел 5 Водоотведение
- •21. Основы канализации
- •22. Уловители нефтепродуктов
- •Литература
- •Содержание
3.3. Основное уравнение гидростатики. Эпюры гидростатического давления
Это уравнение есть уравнение равновесия жидкости, находящейся под действием только сил тяжести.
В уравнении Эйлера (3.11) проекции ускорений для земных условий равны:
Х, У = 0; Z = -g.
Тогда уравнение (3.11) можно представить в виде
![]() (3.12)
(3.12)
Уравнение
(3.12) является дифференциальным уравнением
равновесия жидкости, находящейся под
действием сил тяжести. Преобразуем его.
поскольку![]() ,
то
,
то
![]() ,
т.е. в любом случае
,
т.е. в любом случае
![]() всегда остается величиной постоянной,
но запишем ее по-иному:
всегда остается величиной постоянной,
но запишем ее по-иному:
![]() =
idem;
(3.13)
=
idem;
(3.13)
idem
– здесь и в дальнейшем употребляется
только в смысле «одно и то же», т.е.
имеющее одно и то же значение в
рассматриваемой области (в объеме или
на линии) лишь в данный момент времени,
в отличие от const,
означающей постоянство величины во
времени. В выражении (3.13) Z
– геометрический напор;
![]() - пьезометрический напор;
- пьезометрический напор;![]() - гидростатический напор.
- гидростатический напор.
Проиллюстрируем
величину
![]() рисунком 3.10.
рисунком 3.10.
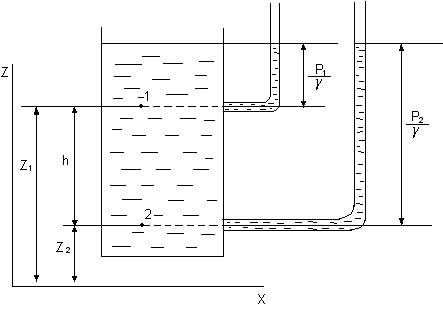
Рис.3.10
Для точек 1 и 2 в сосуде
![]() ;
(3.14)
;
(3.14)
так как Z1 – Z2=h, то
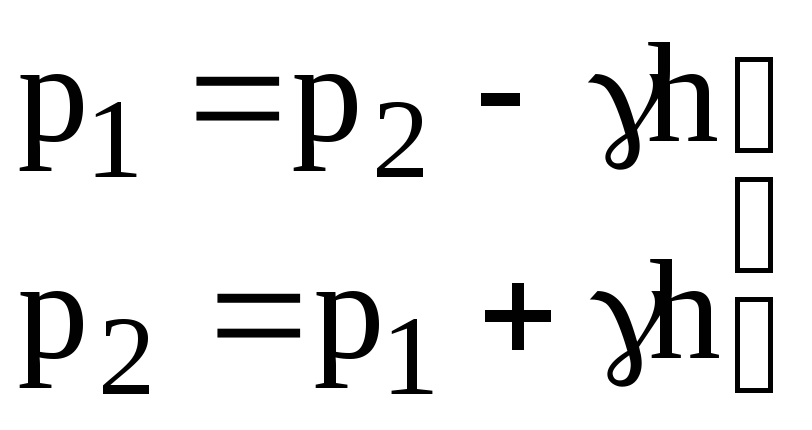 (3.15)
(3.15)
Уравнения (3.13), (3.14) или (3.15) называются основным уравнением гидростатики.
Вывод: потенциальная энергия в любой точке покоящейся жидкости является величиной постоянной.
Эпюры гидростатического давления есть графическое выражение закона изменения давления по глубине жидкости.
Рассмотрим несколько типовых случаев.
1. Сосуд с вертикальными плоскими стенками заполнен жидкостью на глубину h и открыт сверху, т.е. на поверхности действует атмосферное давление рат (рис.3.11).
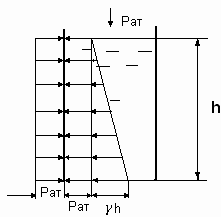
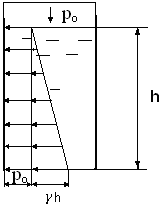
Рис.3.11 Рис.3.12
Согласно уравнению гидростатики атмосферное давление передается равномерно по всей глубине h, а давление от столба жидкости - по линейному закону: p = γh. Так как сосуд окружает среда с атмосферным давлением, то действие атмосферного давления через жидкость на стенки компенсируется давлением извне, т.е. силовое воздействие на стенки сосуда окажет только давление столба жидкости.
Гидростатическое давление направлено по нормали к стенкам сосуда согласно его свойству.
2. Сосуд с вертикальными плоскими стенками заполнен жидкостью, на поверхности которой создано избыточное давление ро (рис.3.12). В этом случае силовое воздействие на стенки оказывает как избыточное давление на поверхности, так и давление от столба жидкости.
3. Сосуд с наклонной плоской поверхностью, открытый сверху (рис.3.13).
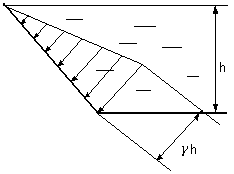
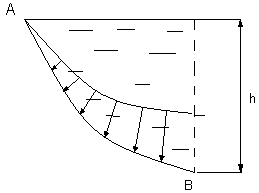
Рис.3.13 рис.3.14
Построение эпюры аналогично предыдущим случаям.
4. Сосуд, стенка (стенки) которого имеет криволинейную поверхность, например АВ (рис.3.14).
Для построения эпюры гидростатического давления, действующего на поверхность АВ, необходимо через определенный интервал по глубине h провести касательные плоскости к кривизне поверхности и к ним по нормали линии действия давления. Закон изменения давления в этом случае повторит форму криволинейной поверхности.
3.4. Сила гидростатического давления на плоские поверхности
Давление, созданное в жидкости, действуя на поверхности различных устройств и их элементов, создает силу. Плоскими поверхностями могут быть стенки различных резервуаров, тела плотин, клапаны, щиты и затворы.
Определим величину силы, действующей на плоскую поверхность, и точку ее приложения.
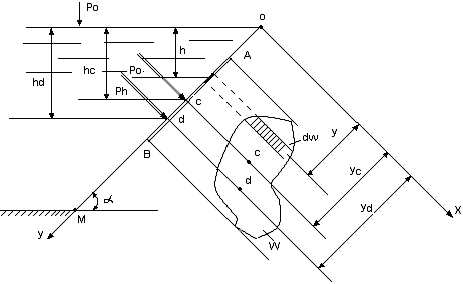
Рис.3.15
Представим (рис.3.15) сосуд, наполненный жидкостью и имеющий плоскую стенку ОМ под углом α к горизонту. В плоскости этой стенки наметим оси координат ОУ и ОХ. Ось ОХ направим перпендикулярно к плоскости чертежа.
На стенке сосуда наметим некоторую плоскую фигуру АВ любого очертания, имеющую площадь . Из точки О проведем ось ОХ, нормальную к направлению АВ, т.е. ось ОХ совместим с плоскостью чертежа. Будем мысленно вращать фигуру АВ вокруг оси ОУ так, чтобы эта фигура совместилась с плоскостью чертежа.
Выделим на площади фигуры бесконечно малую поверхность в виде полоски d, погруженную на глубину h. При этом расстояние полоски от оси ОХ равно y. гидростатическое давление в области бесконечно малой плоскости согласно основному уравнению гидростатики будет
![]() .
.
Тогда сила давления на элементарную площадку
![]() .
(3.16)
.
(3.16)
Интегрируя выражение (3.16) в пределах площади ω и заменив h = у·sinα, получим
![]() .
(3.17)
.
(3.17)
Интеграл
![]() представляет собой статический момент
площади фигуры АВ относительно оси ОХ.
Из механики известно, что
представляет собой статический момент
площади фигуры АВ относительно оси ОХ.
Из механики известно, что
![]() =
yс,
=
yс,![]() (3.18)
(3.18)
где ус – расстояние центра тяжести площади фигуры АВ относительно оси ОХ.
Подставив (3.18) в (3.17) и заменив ycsinα = hc, получим силу, действующую на площадь ω:
![]() (3.19)
(3.19)
Это означает, что сила давления P жидкости на плоскую фигуру, погруженную в жидкость, равна произведению этой площади ω на гидростатическое давление в ее центре тяжести (po+γhc).
Из формулы (3.19) следует, что сила Р состоит из двух сил: силы роω и силы γhсω. Сила pоω создает равномерную нагрузку и приложена в центре тяжести фигуры площадью ω. Сила γhсω создает неравномерную нагрузку и поэтому точка ее приложения не совпадает с центром тяжести фигуры. Эта точка называется центром гидростатического давления; обозначается она буквой d. Для нахождения точки приложения силы γhсω применим теорему механики о моменте равнодействующей силы: момент равнодействующей силы относительно оси ОХ равен сумме моментов от элементарных сил:
![]() .
(3.20)
.
(3.20)
Интеграл
![]() представляет собой момент инерцииIx
площади ω относительно оси ОХ. Из механики
известно, что
представляет собой момент инерцииIx
площади ω относительно оси ОХ. Из механики
известно, что
![]()
![]() ,
(3.21)
,
(3.21)
где Ic - момент инерции площади относительно оси ОХ, проходящей через центр тяжести.
Подставим выражение (3.21) в (3.20):
![]() .
(3.22)
.
(3.22)
Из
выражения (3.22) следует, что центр
гидростатического давления yd
находится ниже центра тяжести на величину
эксцентриситета
![]() .
.
