shpory_traktora
.doc
|
1,3) при использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями. а) Цепи с последовательным соединением резистивных элементов. При
последовательном соединении нелинейных
резисторов в качестве общего аргумента
принимается ток, протекающий через
последовательно соединенные элементы.
Расчет проводится в следующей
последовательности. По заданным
ВАХ
|
1,4) Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем: Строятся
графики зависимостей Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений. В
качестве примера рассмотрим цепь на
рис. 5. Для нее выражаем напряжения
на резистивных элементах в функции
Далее
задаемся током, протекающим через
один из резисторов, например во второй
ветви
|
2,1) Аналитический (графический) метод расчета по первым гармоникам токов и напряжений. В этом методе по сложному закону изменяющиеся токи и напряжения на нелинейном элементе заменяют их первыми гармониками. В расчете используют ВАХ по первым гармоникам в аналитической форме или в виде графической зависимости. Основные этапы расчета в аналитическом варианте: 1) выражают аналитически ВАХ нелинейного элемента для мгновенных значений; 2) путем подстановки в нее первой гармоники напряжения или тока получают формулу, которая дает нелинейную связь между амплитудой первой гармоники тока через нелинейный элемент и амплитудой первой гармоники напряжения на нем [в качестве примера такой связи можно назвать формулу (15.19)]; 3) в уравнение, составленное для исследуемой цепи по второму закону Кирхгофа, подставляют вместо мгновенных значений тока и напряжения на нелинейном элементе мгновенные значения их первых гармоник, а высшими гармониками пренебрегают; 4) уравнение разбивают на два уравнения: одно из них выражает собой равенство коэффициентов при синусных слагаемых левой и правой частей уравнения, другое — равенство коэффициентов при косинусных слагаемых обеих частей уравнения; 5) совместно решают эти два уравнения. Основные этапы расчета в графическом варианте: 1) в качестве зависимости между амплитудой первой гармоники напряжения на нелинейном элементе и амплитудой первой гармоники тока через него берется нелинейная зависимость в виде графика. Эта зависимость может быть получена любым путем, в том числе и опытным;
2)
произвольно задаются амплитудой
3)
путем построения нескольких векторных
диаграмм для различных значений Данный метод позволяет рассматривать такие нелинейные явления, как преобразование постоянного тока в переменными обратное преобразование, явление резонанса на основной гармонике, триггерный эффект на первой гармонике, некоторые типы автомодуляционных процессов. Но он не позволяет исследовать более сложные явления, как, например, резонанс на высших, низших или дробных гармониках и др.
|
|
2,2) Для расчета электрических цепей любой сложности, содержащих только один нелинейный элемент, может быть применен метод эквивалентного генератора. Относительно нелинейного элемента всю остальную часть схемы можно заменить эквивалентным генератором напряжения, ЭДС которого равна напряжению на разомкнутых зажимах ветви с нелинейным элементом, а его внутреннее сопротивление равно входному сопротивлению пассивного линейного двухполюсника относительно разомкнутой ветви с нелинейным элементом. Так как определение напряжения холостого хода и входного сопротивления проводится при исключенном из рассмотрения нелинейном элементе, то эти этапы расчета являются чисто линейными задачами. Таким образом, сложная схема сводится к схеме, представленной на рис. 1.1. Определение же тока в нелинейном элементе и напряжения на нем проводится графическим методом.
Запишем
для схемы (рис. 1.1) уравнение по второму
закону Кирхгофа:
Ток
в схеме (и напряжение на нелинейном
элементе) можно определить по найденному
значению ЭДС, построив линейную
зависимость
Однако
расчет можно упростить, если исходное
уравнение привести к виду:
В
этом случае решение задачи, то есть
определение тока и напряжения на
нелинейном элементе, - это точка
пересечения вольт-амперной характеристики
(ВАХ) нелинейного элемента (НЭ) и
линейной вольт-амперной характеристики
эквивалентного генератора
|
2,3) Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории. Возможны
различные критерии статистической
эквивалентности, которые могут быть
положены в основу метода статистической
линеаризации. В тех случаях, когда
линеаризуют безынерционный нелинейный
элемент, у которого нелинейная
зависимость между входным
где 1. Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента. 2. Критерий минимума математического ожидания квадрата разности случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного элемента. Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными. 3,1) Под нелинейными индуктивными элементами понимают индуктивные катушки с обмотками, намотанными на замкнутые сердечники из ферромагнитного материала, для которых зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейна. Индуктивное сопротивление таких катушек, оказываемое прохождению переменного тока, не постоянно; оно зависит от значения переменного тока. Условимся называть их нелинейными индуктивными катушками. Нелинейные индуктивные катушки подразделяют на управляемые и неуправляемые, но деление на безынерционные и инерционные на них не распространяется, так как их нелинейность обусловлена свойствами ферромагнитного материала, а не тепловым эффектом.
|
3,2) Потери в ферромагнитном сердечнике, обусловленные гистерезисом. Как известно (см. § 14.4), ферромагнитным материалам свойственно явление гистерезиса, которое вызвано отставанием изменения магнитной индукции от изменения напряженности магнитного поля. Площадь гистерезисной петли в координатах В, Н (В — индукция, Н — напряженность поля), снятая при достаточно медленном изменении магнитного поля во времени (когда вихревые токи практически отсутствуют), характеризует энергию, выделяющуюся в единице объема ферромагнитного материала за один период переменного тока (за одно перемагничивание). Потери в сердечнике, обусловленные гистерезисом, пропорциональны объему сердечника, первой степени частоты и площади гистерезисной петли. От толщины листов потери на гистерезис не зависят. Гистерезисные петли при достаточно быстром изменении магнитного поля во времени называют динамическими. Динамические петли шире соответствующих статических за счет вихревых токов и магнитной вязкости. Степень отличия динамической петли от соответствующей статической зависит от скорости перемагничивания (от частоты), удельного электрического сопротивления материал а, толщины листов, температуры и наличия в магнитном потоке высших гармоник 3,3) Влияние гистерезиса и вихревых токов на ток катушки с ферромагнитным сердечником Магнитный гистерезис вносит дополнительные изменения в форму кривой намагничивающего тока. Эти изменения обусловлены тем, что при увеличении магнитного потока ход кривой тока определяется восходящей, а при уменьшении потока – нисходящей ветвью петли гистерезиса. Ток в катушке с учетом магнитного гистерезиса
|
|
3,4)
Параллельная
4,1) Явление изменения знака угла сдвига фаз между первыми гармониками напряжения и гармониками тока при изменении напряжения или тока источника питания, которая обусловлена нелинейностью катушки с ферромагнитным сердечником, называется феррорезонансом напряжений. В линейной цепи такое явление принципиально невозможно. Как известно, резонанс напряжений в линейной цепи можно добиться путем изменения емкости конденсатора, индуктивности катушки или частоты напряжения питания. В отличие от цепей с постоянными параметрами резонанс в рассматриваемой цепи может быть достигнут путем изменения значения приложенного напряжения. Индуктивность катушки с ферромагнитным сердечником имеет зависимость от значения тока, и, следовательно, изменится при изменении напряжения всей цепи.
|
4,2) Феррорезонанс токов возникает в цепи с параллельным соединением конденсатора и катушки с ферромагнитным сердечником. Катушка с ферромагнитным сердечником представляет собой нелинейный элемент. Если катушку с ферромагнитным сердечником и конденсатор соединим параллельно, то в сложенном контуре при плавном изменении напряжения может наступить резонанс вследствие взаимной компенсации реактивных составляющих токов катушки и конденсатора, это явление получило название феррорезонанса токов. В ветке, содержащий катушку с ферромагнитным сердечником, при синусоидальной напряжению источника питания ток несинусоидальный. В ветке с конденсатором он изменяется по синусоидальной законом. Поэтому резонансный режим возможен для той из гармоник несинусоидальных тока в ветви с катушкой, совпадает с частотой синусоидального тока в ветви с конденсатором. Чтобы можно было достичь феррорезонанса для основной гармоники тока катушки и конденсатора, необходимо, чтобы вольт-амперные характеристики катушки с ферромагнитным сердечником и конденсатора пересекались. 4,3) Стабилизатор, у которого на зажимах нелинейного дросселя получают стабилизированное напряжение, является простейшим ферромагнитным стабилизатором. Его основной недостаток — низкий коэффициент мощности. Кроме того, при больших токах в цепи габариты линейного дросселя очень большие. Для уменьшения веса и габаритов ферромагнитные стабилизаторы напряжения изготовляют с объединенной магнитной системой, а для повышения коэффициента мощности включают конденсатор по схеме резонанса токов. Такой стабилизатор называется феррорезонансным. Феррорезонансные стабилизаторы напряжения конструктивно похожи на обычные трансформаторы
|
РАЗДЕЛ 6 1,1) Электрическими линиями с распределенными параметрами называют такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой, соседней точке. Под магнитными линиями с распределенными параметрами понимают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней. В электрических линиях с распределенными параметрами продольные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих друг другу участков линии длиной dx. Поперечные сопротивления состоят из сопротивлений утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии. В магнитных линиях с распределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образующих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими другдругу участками линии. 1,2) Электрические свойства длинной линии характеризуются первичными параметрами, т.е. параметрами, отнесёнными к единице длины линии(1 км в линиях проводной связи и 1м в радиосвязи). Первичными параметрами являются: резистивное сопротивление единицы длины линии R – это сопротивление проводов линии единичной длинны. индуктивность единицы длины линии L – определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызывающему этот поток. (Гн/км) ёмкость единицы длины линии C – определяется отношением заряда, приходящегося на ед-цу длины линии, к напряжению между проводами линии.(Ф/км) проводимость изоляции единицы длины линии G – обусловлена несовершенством изоляции и представляет собой активную составляющую проводимости изоляции между проводами, отнесённую к единице длины линии. Если первичные параметры остаются пост на протяжении всей ее длины, то линия- однородная |
||||
|
2,2) Входное сопротивление линии Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
Рассмотрим некоторые частные режимы работы линии. При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее. Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.16) упрощается и принимает вид
В
случае разомкнутых выходных зажимов
(Zн = бесконечность)
Когда
линия нагружена на произвольное
сопротивление, не равное волновому
(Zн <> Zв), можно пользоваться для
расчетов общей формулой (13.16). Однако
иногда удобно выразить Zвх через
параметры XX и КЗ. Для этого разделим
числитель и знаменатель (13.16) на Данная формула позволяет по измеренным значениям сопротивлений XX и КЗ рассчитать входное сопротивление линии. Существует еще одна форма представления входного сопротивления. Для получения ее перепишем |
выражение (13.16) после деления на
в другом виде:
Обозначим
Тогда
|
2,3) Согласованная нагрузка линии Если в конце линии включено сопротивление нагрузки, равное волновому:
то, обращаясь к формулам (18-23), находим, что
т. е. отраженная волна не возникает Такую нагрузку называют согласованной нагрузкой или нагрузкой без отражения.
При
этом, как следует из (18-47), коэффициент
отражения Из написанных выше соотношений с учетом (18-48) получим:
Отсюда следует:
т.
е. для любой точки линии отношение
комплексов
Из
соотношения (18-31) следует, что для
согласованной линии
Полагая
начальную фазу напряжения в конце
линии равной нулю, т. е.
Полученные
соотношения изображены на рис. 18-9.
Точки пересечения оси абсцисс с
кривыми напряжения и тока сдвинуты
на расстояние |
|
фазе.
Рис. 18-9. Мощность, проходящая через какое-нибудь сечение линии,
Эта мощность уменьшается по мере удаления от начала, так как на каждом элементе длины линии поглощается мощность
равная
сумме потерь в сопротивлении проводов
и в проводимости изоляции на элементе
линии
Мощность,
передаваемая по согласованной линии,
называется естественной или натуральной
мощностью. Режим передачи естественной
мощности может иметь место в линиях,
если сопротивление нагрузки равно
волновому сопротивлению
Мощность,
получаемая линией,
Мощность
в конце линий На основании равенств (18-49) и (18-50)
к.
п. д. линии Все сказанное здесь о согласованной линии применимо и к бесконечно длинной линии, поскольку в последней не может возникнуть Отраженная волна.
|
2,4) ЛИНИЯ БЕЗ ИСКАЖЕНИЯ В таких линиях волны всех частот распространяются с одинаковой фазовой скоростью и затухают в равной степени. При движении электромагнитной волны по линии без искажений волна напряжения и волна тока уменьшаются по амплитуде, но формы волн в начале и в конце линии подобны. Неискажающие линии находят применение в телефонии. При телефонном разговоре по таким линиям не искажается тембр голоса, т.е. не искажается спектральный состав речи. Для того чтобы линия была неискажающей коэффициент затухания и фазовая скорость vф не должны зависеть от частоты. Это выполняется, если между параметрами линии существует соотношение:
По определению:
Из (13.37) следует, что коэффициент затухания и фазовая скорость vф в линии без искажений действительно не зависят от частоты. Волновое сопротивление
также не зависит от частоты.
|
2,5) ЛИНИЯ БЕЗ ПОТЕРЬ В РАЗЛИЧНЫХ РЕЖИМАХ РАБОТЫ Для линии без потерь при = 0, = j соотношения для тока и напряжения вдоль линии можно представить в виде:
Выразим
При x' = l отсюда получим значения напряжения и тока в начале линии. Входное сопротивление линии без потерь, следовательно, можно выразить как
или
с учетом соотношения выходных величин
|

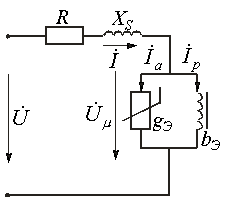 Последовательная
Последовательная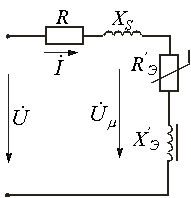
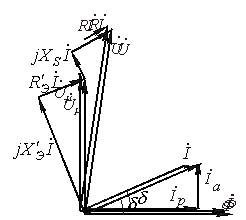 векторная
диаграмма
векторная
диаграмма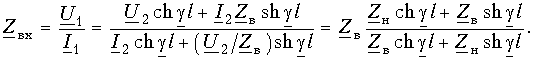
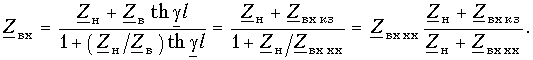
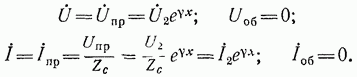 (18-49)
(18-49)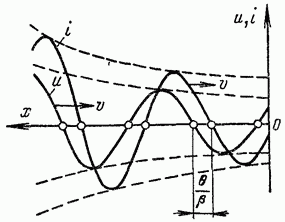
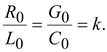 (13.36)
(13.36)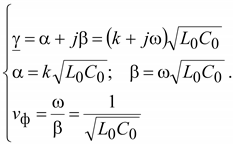 (13.37)
(13.37)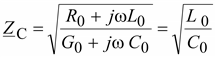 (13.38)
(13.38)