6. Гидравлический расчет трубопроводов

6.1. Классификация трубопроводов

В зависимости от соотношения линейных и местных потерь трубопроводы делятся на короткие и длинные, в зависимости от конструкции гидравлической системы - на простые и сложные.

короткие трубопроводы – это трубопроводы сравнительно небольшой длины, на которых смонтировано значительное количество местных сопротивлений и поэтому местные потери сопоставимы с линейными. Это, например, системы объемных гидравлических приводов всех назначений, системы смазки различных устройств.

Кроме того, это трубопроводы, некорректный расчет которых может вызвать отказ работы устройства (сифоны, всасывающие линии насосов и т.п.).

при расчете коротких трубопроводов учитываются как линейные, так и местные потери:

h_сум = Σh_л.п+Σh_м.п.

задачи решаются с применением уравнений неразрывности и Д.Бернулли для потока реальной жидкости.

Длинные трубопроводы – это трубопроводы значительной длины, в которых линейные потери являются основными. Это водопроводные системы всех назначений, нефтепроводы и т.п. системы.

При расчете таких трубопроводов определяются только линейные потери, а на местные добавляют 5…10% от линейных, т.е.

h_сум = (1,05…1,1)h_л.п.

Простые трубопроводы – это трубопроводы, как правило, одного диаметра, не имеющие ответвлений.

Сложные трубопроводы имеют различного рода ответвления или состоят из нескольких линий (параллельного соединения, тупиковые, замкнутые, или кольцевые).

6.2. Расходная характеристика трубопровода (модуль расхода)

Вспомним формулу линейных потерь – формулу Дарси – Вейсбаха: .

Выразим в этой формуле скорость V через расход Q из соотношения :

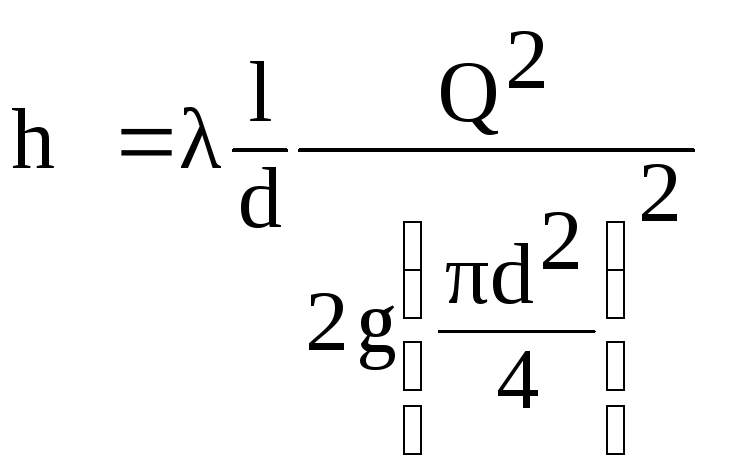. (6.1)

Для трубопровода определенного диаметра комплекс величин в выражении (6.1) можно считать величиной постоянной (1/К²), кроме коэффициента гидравлического трения λ. На основании понятия среднеэкономической скорости V_с.э покажем, что и указанный коэффициент λ можно отнести к этому комплексу, т.к. в этом случае, число Рейнольдса будет иметь определенное значение: , и на графике Никурадзе коэффициент λ в этом случае будет иметь конкретное значение.

Обоснуем правомерность введения понятия среднеэкономической скорости следующими рассуждениями.

Гидравлическую систему, например водопроводную, для пропуска определенного расхода можно выполнить из труб разного диаметра. При этом с увеличением диаметра d, следовательно, уменьшением скорости V капитальные затраты будут расти, а эксплуатационные затраты будут уменьшаться из-за снижения гидравлических потерь. Скорость, при которой суммарные затраты будут иметь минимальное значение, будем называть среднеэкономической скоростью V_с.э = 0,8…1,3 м/с (рис.6.1).

рис.6.1

Тогда формула линейных потерь (6.1) примет вид

, (6.2)

где К – расходная характеристика трубопровода (модуль расхода), зависит от материала трубопровода, диаметра и расхода. берется из таблиц.

6.3. Гидравлические характеристики трубопроводов

Гидравлической характеристикой трубопровода называется зависимость напора, который необходимо создать в трубопроводе для пропуска по нему определенного расхода, т.е. Н=f(Q).

Рассмотрим некоторые особенности этой характеристики.

1. Представим себе горизонтальный трубопровод длиной l и диаметром d, питаемый, например, от насоса с постоянным расходом Q (рис.6.2).

рис. 6.2

Составив уравнение Бернулли для сечений 1-1 и 2-2, получим, что напор в сечении 1-1 тратится на преодоление линейных потерь h_л.п, т.е. Н = h_л.п.. тогда формулу (6.2) представим в виде

. (6.3)

Обозначим . Для конкретного трубопровода это будет постоянная величина, тогда выражение (6.3) примет вид

. (6.4)

Такая явно квадратичная зависимость свойственна только турбулентному режиму движения (рис.6.3).

рис. 6.3

Из рис. 6.3 видно, что, например, для пропуска расхода Q_i в трубопроводе необходимо создать напор Н_i.

2.Допустим, что насос подает жидкость в трубопровод с преодолением статического напора Н_ст (рис.6.4).

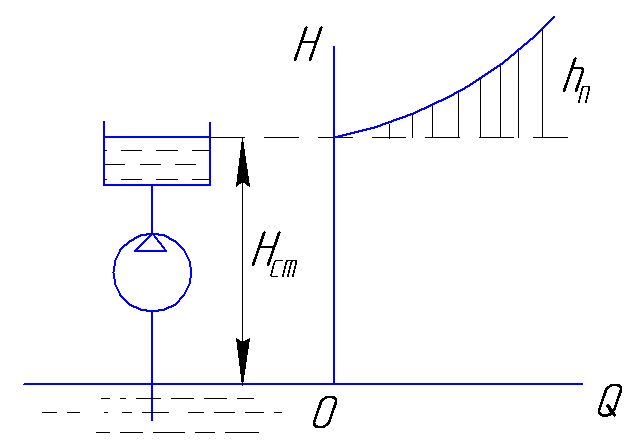
рис. 6.4

Сначала характеристика совпадает с линией ОН (ординатой). Дальнейшее увеличение напора расходуется на преодоление гидравлических сопротивлений h_п, которые увеличиваются с увеличением расхода Q. Таким образом, аналитическое выражение такой характеристики будет иметь вид

. (6.5)

3. мы имеем, например, семейство характеристик 1,2,3 (рис.6.5). Простой анализ позволяет сделать вывод, что они принадлежат трубопроводам различного диаметра, т.е. d₁>d₂>d₃. Таким образом, например, трубопровод 1 может пропустить больший расход при меньшем напоре, чем трубопроводы 2 и 3.

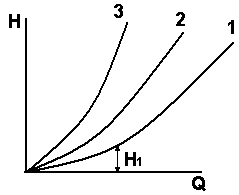
Рис. 6.5 Рис. 6.6

4. Гидравлическую характеристику трубопровода определенного диаметра можно изменить, например, с помощью задвижки. В выражении Н=ВQ² изменяется коэффициент В. Задвижкой в этом случае вводится дополнительное сопротивление, эквивалентное определенной длине трубопровода (рис.6.6).

5. Примем, что насос подает жидкость в трубопровод с верхнего бака в нижний (рис.6.7), т.е. имеет место «отрицательного» статического напора. В этом случае напор Н` без насоса обеспечит расход в трубопроводе Q`. Для увеличения расхода подключается насос.

Рис. 6.7

6. гидравлическая сеть состоит из нескольких трубопроводов различного диаметра и длины, соединенных последовательно (рис.6.8).

Рис. 6.8

Очевидно, что ;;

. (6.6)

Суммарную характеристику можно получить по выражению (6.6) или построением характеристик отдельных ее участков 1,2 и 3 с последующим графическим их сложением (рис.6.9).

Рис. 6.9

7. гидравлическая сеть состоит из нескольких трубопроводов различного диаметра и длины, соединенных параллельно (рис. 6.10).

Рис. 6.10

Очевидно, что . В точках А и В напор одинаков для трубопровода с расходомQ₁ и Q₂. следовательно, падение напора в каждой ветке одинаково, т.е. Н=Н₁=Н₂ или

. (6.7)

Суммарную характеристику получают построением характеристик отдельных ее участков с последующим графическим их сложением (рис.6.11).

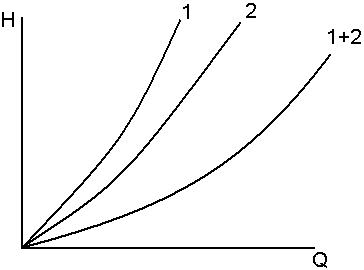
Рис. 6.11