
ЛабИнф1-3
.pdf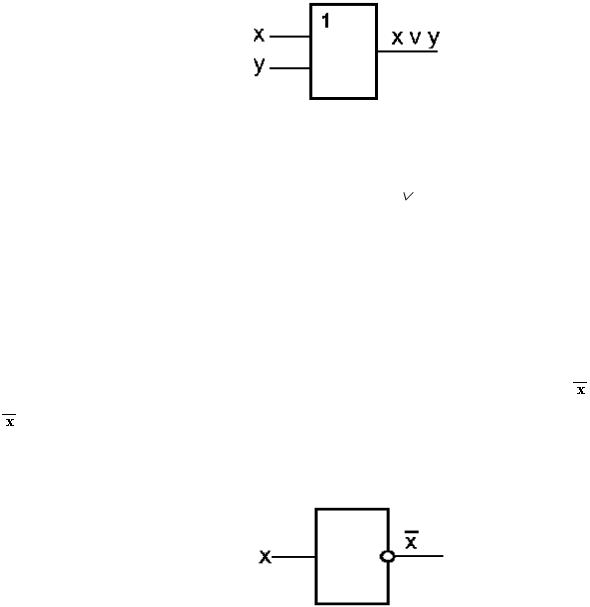
41
|
|
Рис. 2.2 |
|
Таблица истинности схемы ИЛИ |
|
||
|
|
|
|
|
x |
y |
x y |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
Схема НЕ (инвертор) реализует операцию отрицания. Связь между вхо-
дом x этой схемы и выходом |
z можно записать соотношением |
z = , x где |
читается как "не x" или "инверсия х". |
|
|
Если на входе схемы 0, |
то на выходе 1. Когда на входе 1, |
на выходе 0. |
Условное обозначение на структурных схемах инвертора — на рисунке 2.3
|
|
Рис. 2.3 |
|
Таблица истинности схемы НЕ |
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
||
|
0 |
|
1 |
|
|
|
|
|
|
||
|
1 |
|
0 |
|
|
|
|
Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрица-
ние результата схемы И. Связь между выходом z и входами x и y схемы записы-
вают следующим образом:  , где
, где  читается как "инверсия x и y".
читается как "инверсия x и y".

42
Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 2.4.
Рис. 2.4
Таблица истинности схемы И–НЕ
x |
y |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y
схемы записывают следующим образом:  , где
, где  , читается как
, читается как
"инверсия x или y ". Условное обозначение на структурных схемах схемы
ИЛИ—НЕ с двумя входами представлено на рис. 2.5.
Рис. 2.5
Таблица истинности схемы ИЛИ—НЕ |
|
||
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
43
Триггер и суматор
Триггер – это электронная схема, широко применяемая в регистрах компь-
ютера для надѐжного запоминания одного разряда двоичного кода. Триггер име-
ет два устойчивых состояния, одно из которых соответствует двоичной единице,
а другое – двоичному нулю.
Термин триггер происходит от английского слова trigger – защѐлка, спус-
ковой крючок. Для обозначения этой схемы в английском языке чаще употреб-
ляется термин flip-flop, что в переводе означает ―хлопанье‖. Это звукоподража-
тельное название электронной схемы указывает на еѐ способность почти мгно-
венно переходить (―перебрасываться‖) из одного электрического состояния в другое и наоборот.
Сумматор — это электронная логическая схема, выполняющая суммиро-
вание двоичных чисел.
Сумматор служит, прежде всего, центральным узлом арифметико-
логического устройства компьютера, однако он находит применение также и в других устройствах машины.
Многоразрядный двоичный сумматор, предназначенный для сложения
многоразрядных двоичных чисел, представляет собой комбинацию однораз-
рядных сумматоров, с рассмотрения которых мы и начнѐм. Условное обозначе-
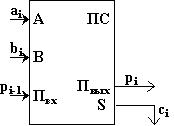
ние одноразрядного сумматора на рис. 2.8.
Рис. 2.8
Одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами.
Основные законы алгебры логики
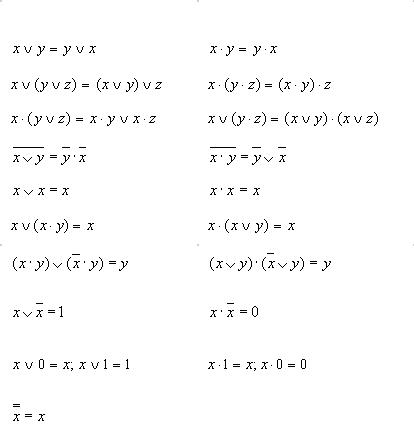
|
|
|
44 |
|
|
|
|
|
|
Закон |
|
Для ИЛИ |
|
Для И |
|
|
|
|
|
|
|
|
||
Переместительный |
|
|
|
|
|
|
|
|
|
|
|
|
||
Сочетательный |
|
|
|
|
|
|
|
|
|
|
|
|
||
Распределительный |
|
|
|
|
|
|
|
|
|
|
|
|
||
Правила де Моргана |
|
|
|
|
|
|
|
|
|
|
|
|
||
Идемпотенции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поглощения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Склеивания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Операция |
перемен- |
|
|
|
ной с ее инверсией |
|
|
|
|
|
|
|
|
|
|
|
|
||
Операция с констан- |
|
|
|
|
тами |
|
|
|
|
|
|
|
|
|
|
|
|
||
Двойного отрицания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблицы истинности
Согласно определению, таблица истинности логической формулы вы-
ражает соответствие между всевозможными наборами значений перемен-
ных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь. Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таб-
лица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1. Составить таблицу истинности для формулы 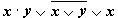

45
Решение: таблица содержит две переменные x и y. В первых двух столб-
цах таблицы запишем четыре возможных пары значений этих переменных, в по-
следующих столбцах – значения промежуточных формул и в последнем столбце
– значение формулы. В результате получим таблицу:
|
|
|
|
|
|
|
|
|
Переменны |
|
Промежуточные логические формулы |
Формула |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из таблицы видно, что при всех наборах значений переменных x и y фор-
мула  принимает значение 1, то есть является тождественно ис-
принимает значение 1, то есть является тождественно ис-
тинной.
Пример 2. Составить таблицу истинности для формулы  .
.
Решение:
|
|
|
|
|
|
|
Переменные |
Промежуточные логические формулы |
Формула |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из таблицы видно, что при всех |
наборах значений переменных x и y фор- |
мула принимает значение 0, |
то есть является тождественно ложной. |
Пример 3. Составить таблицу истинности для формулы  .
.
Решение: таблица содержит три переменные x , y и z. В первых трех столбцах таблицы запишем возможных тройки значений этих переменных.

46
|
|
|
|
|
|
|
|
|
Переменные |
Промежуточные логические формулы |
Формула |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из таблицы видно, что формула |
|
|
|
|
в некоторых случаях прини- |
|||||||||||||||||
мает значение 1, а в некоторых – 0, то есть является выполнимой. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Cоставить логическую схему для выражения: A B C . |
||||||||||||||||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
A B C |
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В С |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Преобразование логических выражений
Равносильные преобразования логических формул имеют то же назначе-
ние, что и преобразования формул в обычной алгебре. Они служат для упроще-
ния формул или приведения их к определѐнному виду путем использования ос-
новных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и экви-
валенции, понимают равносильное преобразование, приводящее к формуле, ко-
торая либо содержит (по сравнению с исходной) меньшее число операций конъ-
юнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

47
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использо-
вание переместительного и сочетательного законов и т.п.), тогда как другие пре-
образования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при
упрощении логических формул:
1)
(законы алгебры логики применяются в следующей последовательности: прави-
ло де Моргана, сочетательный закон, правило операций переменной с еѐ инвер-
сией и правило операций с константами);
2)
(применяется правило де Моргана, выносится за скобки общий множитель, ис-
пользуется правило операций переменной с еѐ инверсией);
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||
5. Самостоятельная работа студентов на занятии |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Задание 1. Построить таблицу истинности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2. Построить таблицу истинности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
X Y Y X Y |
|||||||||||||
1. X X Y X Y Y |
|
|
|||||||||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
X |
Y |
|
X |
|
|
|
|
|
Y |
|||||||||
3. |
X |
|
Y |
X |
|
|
|
|
|
Y |
X |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
X Y |
X Y |
X |
|
|
|
12. |
|
X |
Y |
X |
Y |
|
|
X |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
X Y |
X Y |
|
|
|
|
|
|
|
|
|
|
|
|
13. |
|
Y |
|
|
|
X |
|
Y |
|
|
|
|
|
X |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
X |
|
Y |
X |
Y |
|
|
|
X |
|
|
|
14. |
Y Y |
X |
Y |
|
|
|
X |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
X |
|
|
|
Y |
|
Y |
|
|
|
|
|
|
|
X Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
15. |
|
X |
Y |
|
X |
|
|
|
|
|
Y |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8. |
X |
|
|
|
Y |
|
|
Y |
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. |
|
X |
Y |
|
X |
Y |
|
|
X |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9. |
X Y |
X |
|
|
|
Y |
Y |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
17. |
|
X |
Y |
|
X |
|
|
Y |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10. |
Y |
|
|
|
X |
|
|
|
Y |
|
|
Y |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задание 3. Построить таблицу истинности и составить логическую схему для
выражения:
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
B |
|
|
C |
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
A B |
|
C |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
A |
|
B C |
|
A |
|
|
|
B |
|
|
C |
|||||||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B C A |
12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
|
B C |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
A |
|
B C |
13. A |
|
B C |
|||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A B |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
14. |
A B |
|
C |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
15. A |
|
B C |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
C |
16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
C |
|
B |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B C |
17. |
|
A |
|
|
|
C |
|
|
B |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
A |
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6.Вопросы для контроля
1.Что такое алгебра логики?
2.Что такое логическая формула?
3.Какая связь между алгеброй логики и двоичным кодированием?
4.В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды?
5.Что такое логический элемент компьютера?
6.Что такое триггер?
7.Что такое сумматор?
8.Какие основные законы выполняются в алгебре логики?
49
9.Как составить таблицу истинности?
7.Задание на дом
1.Лекция по теме «Программные продукты и их классификация. Системное программное обеспечение. Операционные системы».
2.Подготовиться к лабораторной работе «Операционные системы: назначение, основные функции. Работа с файлами и папками»
50
Библиографический список
1. Информатика: учебник/ Н.В. Макарова [и др.]; под ред. Н.В. Макаро-
вой. – 3-е изд. перераб. – М.: Финансы и статистика, 2011. – 768 с.
2. Информатика: практикум по технологии работы на компьютере/ Н.В.
Макарова [и др.]. – М.: Финансы и статистика, 2011. – 256 с.
3. Воронина, С.В. Математика и информатика: методические указания к практическим занятиям по курсу «Математика и информатика» (для студентов дневного отделения)/С.В. Воронина, В.Т. Казуб.– Пятигорск: Пятигорская ГФА,
2008.–103 с.
