
- •Раздел 1. Основные понятия теории вероятностей
- •Тема 1. Пространство элементарных исходов и события. Операции над событиями и отношения между ними
- •Тема 2. Классическое определение вероятности
- •Тема 3. Геометрическое определение вероятности
- •Тема 4. Теоремы сложения и умножения вероятностей
- •Тема 5. Формулы полной вероятности и байеса
- •Тема 6. Схема бернулли. Предельные теоремы в схеме бернулли
- •Тема 7. Дискретные случайные величины
- •Тема 8. Непрерывные случайные величины
- •Тема 9. Законы распределения случайных величин
Тема 8. Непрерывные случайные величины
Случайная величина ξ называется непрерывной, если ее функция распределения F(х) = P{ < x} непрерывна и дифференцируема для всех хR, за исключением, быть может, конечного или счетного числа точек.
Функция
р(х)
= F
'(х)
=
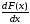 (8.1)
(8.1)
называется плотностью распределения (вероятностей) непрерывной с.в. ξ.
Закон
распределения непрерывной с.в.
может задаваться, наряду с ее функцией
распределения F(х),
также и плотностью распределения р(х),
поскольку, исходя из плотности
распределения р(х),
можем найти ф.р. F(х)
по формуле F(х)
=
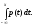 (8.2)
(8.2)
Функция распределения F(x) непрерывной с.в. обладает свойствами, аналогичными свойствам функции распределения дискретной с.в. (кроме свойства 30):
10) определена при всех xR и 0 F(x) 1;
20) является неубывающей функцией: если x1 < x2, то F(x1) F(x2);
30)
является непрерывной функцией:
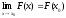 для всехx0R;
для всехx0R;
40)
удовлетворяет предельным соотношениям:
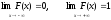 .
.
Плотность распределения р(х) обладает следующими основными (характеристическими) свойствами.
1. Плотность распределения является неотрицательной функцией: р(х) 0 для всех х R. (8.3)
2.
Площадь фигуры, ограниченной графиком
плотности распределения и осью абсцисс,
равна единице:
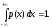 (8.4)
(8.4)
Теорема. Пусть непрерывная с.в. ξ имеет плотность распределения р(х) и функцию распределения F(х). Обозначим через <х1, х2> один из интервалов (конечный или бесконечный) вида [х1, х2], [х1, х2), (х1, х2], (х1, х2). Тогда
Р{ξ<х1,
х2>}
=
F(х2)
–
F(х1)
=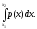 (8.5)
(8.5)
Замечание. Из этой теоремы вытекает, в частности, что если плотность распределения р(х) с.в. ξ нулевая (или функция распределения F(х) постоянна) на некотором интервале <х1, х2>, то с.в. ξ не принимает там значений: P{<x1, x2>} = 0.
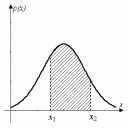
Рис.8.1. Графическая интерпретация
вероятности P{< x1, x2 >}
Вторая часть формулы (8.5) имеет следующий геометрический смысл: вероятность P{<x1, x2>} равна площади криволинейной трапеции, ограниченной графиком плотности распределения p(x), осью абсцисс и прямыми x = x1, x = x2 (на рис. 8.1 заштрихованная
область).
Математическим
ожиданием (средним
значением)
непрерывной
с.в. ξ с плотностью распределения р(х)
называется величина
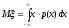 .
(8.6)
.
(8.6)
При этом предполагается, что интеграл в правой части формулы (8.6) абсолютно сходится, т.е.
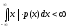 .
(8.7)
.
(8.7)
В противном случае говорят, что математического ожидания у с.в. ξ не существует.
В частности, если все возможные значения непрерывной с.в. ξ принадлежат конечному интервалу (a, b), т.е. p(x) = 0 при x (a, b), то условие (8.7) выполняется и всегда существует
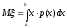 .
(8.8)
.
(8.8)
Дисперсией непрерывной с.в. ξ называется величина Dξ, определяемая равенством
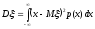 ,
, (8.9)
(8.9)
или
равносильным равенством
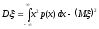 .
. (8.10)
(8.10)
В
частности, если все возможные значения
непрерывной с.в. ξ принадлежат интервалу
(a,
b),
то
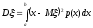 ,
(8.11)
или
,
(8.11)
или
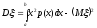 .
. (8.12)
(8.12)
Среднее
квадратическое
(или стандартное)
отклонение
непрерывной с.в.
определяется так же, как и для дискретной
с.в.:
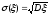 .
.
Математическое ожидание и дисперсия непрерывных с.в. обладают теми же свойствами, что и для дискретных с.в. (см. тему 7).
