Министерство общего и профессионального образования

Российской Федерации

Московский Государственный Институт Электронной Техники

(Технический Университет)

Кафедра ВМ - 2

Дисциплина:

«Специальные разделы

математики»

Домашнее задание

Расчет переходных процессов в электрических нелинейных цепях.

Вариант 15.

Преподаватель:

Фридлендер Б.И.

Выполнил:

ст. гр. ЭКТ- 56М

Фартуков А. М.

Москва, 2001

Оглавление.

Задание. 3

Вариант 15. 3

Выполнение задания. 4

Приложение 1. 10

Литература. 12

Задание.

1. Согласно приведенной электрической схеме построить направленный граф и вывести систему дифференциальных уравнений относительно потокосцеплений и зарядов емкостных элементов.

2. Сравнить полученную систему уравнений с системой, приведенной в варианте.

3. Записать формулы численного решения системы уравнений в варианте неявным разностным методом, а также формулы итерационной коррекции решения на каждом временном шаге.

4. При многошаговой неявной разностной схеме счета вычислить методом Рунге-Кутта значения искомых функций на первых шагах счета.

5. Найти численное решение системы на интервале [ 0; 15 c.] при начальных условиях, указанных в задании, взяв за начальный шаг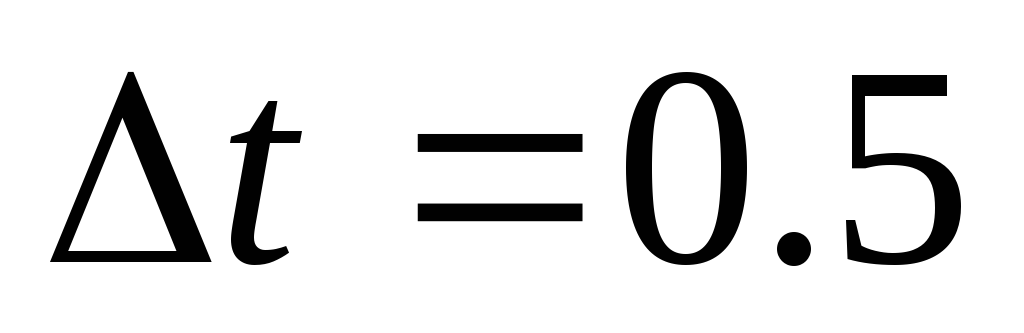с точностью.

6. Построить графики функций по полученным расчетам как в фазовых плоскостях, так и в зависимости от времени.

7. Оформить отчет.

Вариант15.

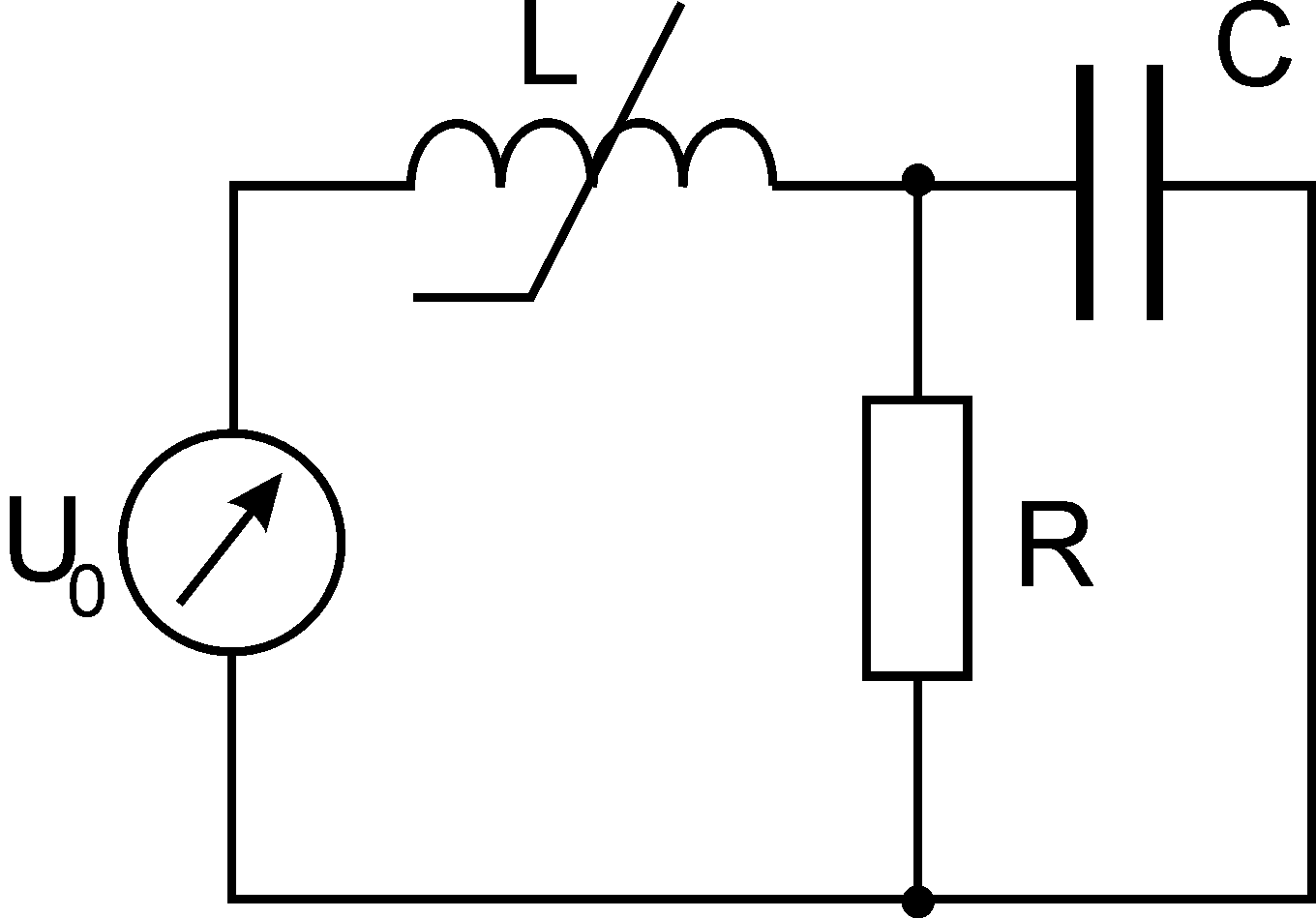
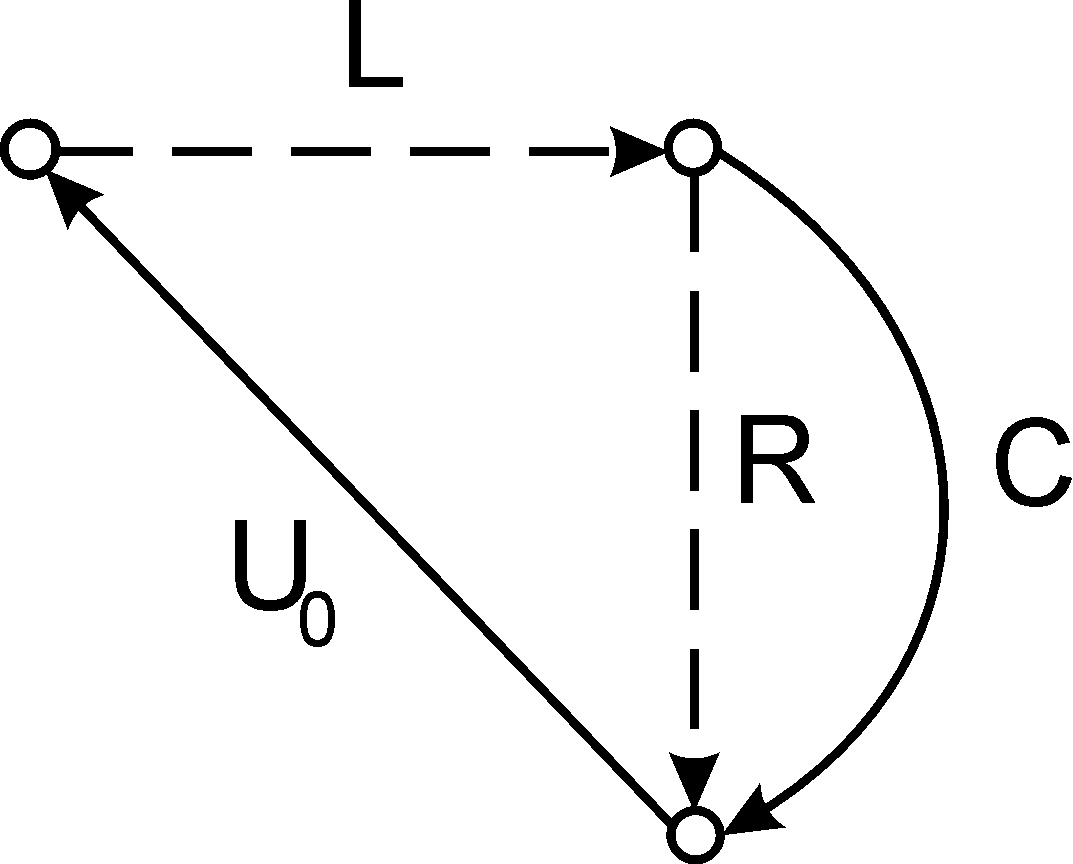
A) b)

Рис. 1. Электронная схема (a) и ее граф с выделенным остовом (b).

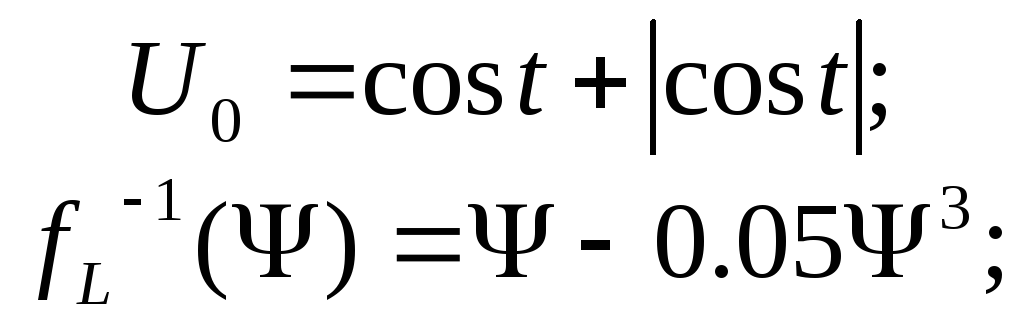
Численно решить систему дифференциальных уравнений неявным методом Гира. Коррекцию решений разностных уравнений на каждом шаге проводить методом Ньютона-Рафсона. Первые шаги счета найти методом Рунге-Кутта. Построить графики

Выполнение задания.

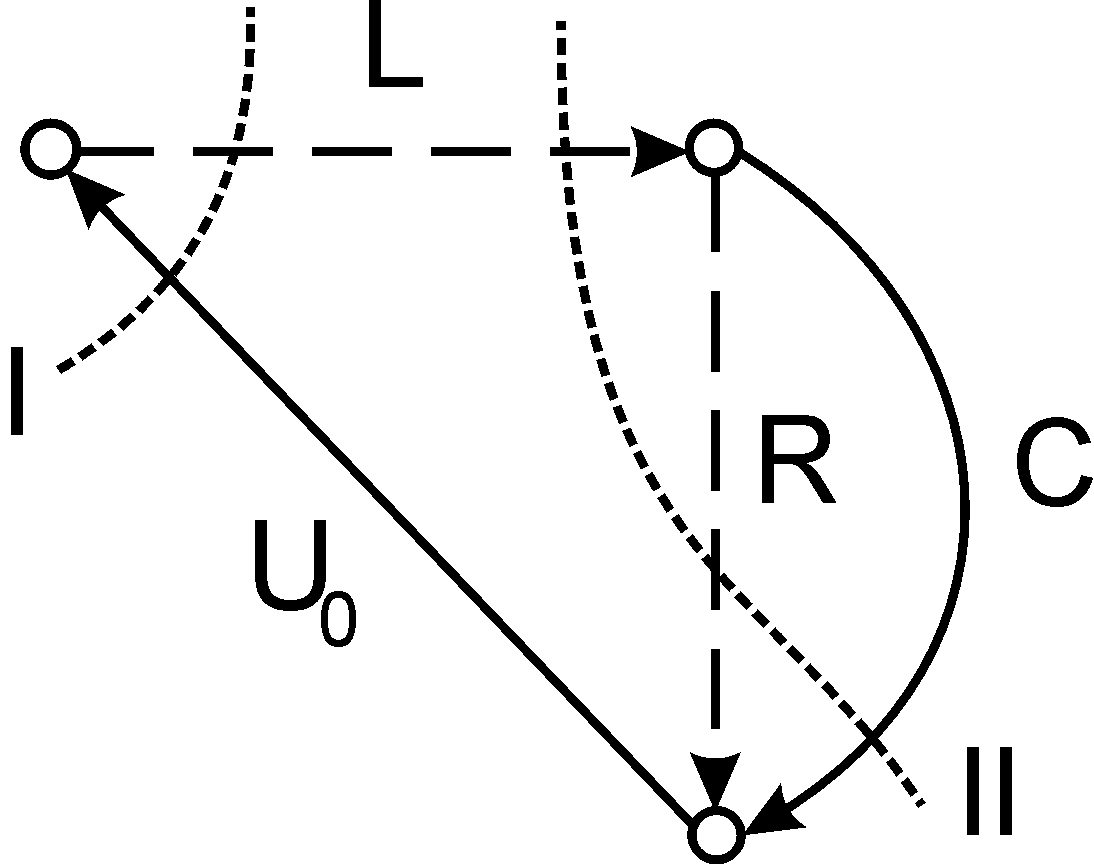
1. Предлагаемый направленный граф схемы приведен на рис. 1, b. Стрелки графа определяют положительные направления токов в элементах схемы. Всего вершин в графеn = 3, следовательно, остов, показанный сплошными линиями, содержитn - 1= 2 ветви. Всего реберm = 4, поэтому число хорд равноm – n + 1= 2. Хорды показаны пунктиром.

A) b)

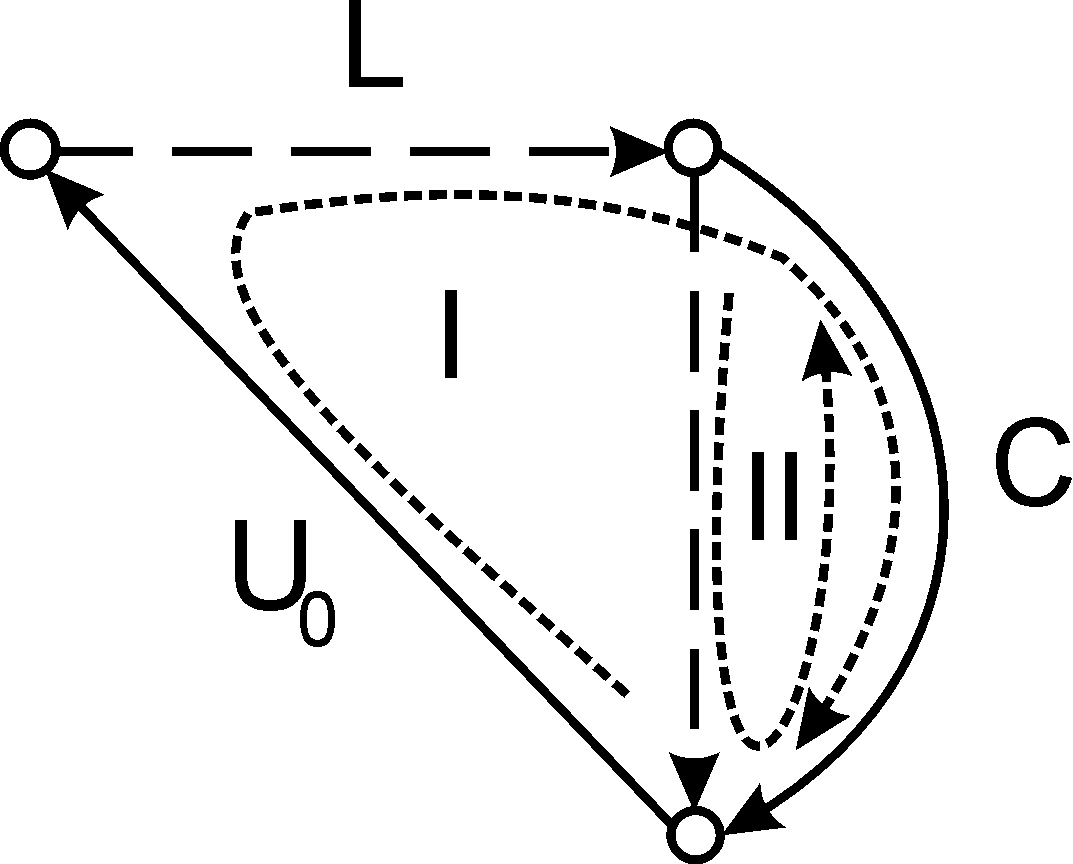
Рис. 2. Граф с фундаментальными разрезами (a) и фундаментальными циклами (b).

Согласно I-ому закону Кирхгофа составим 2 уравнения токов по числу главных сечений, показанных на рис. 2, а:

сечение I: (1)

сечение II: (2)

Согласно II-ому закону Кирхгофа составим уравнения напряжений; по числу хорд имеем 2 главных контура (рис. 2,b):

контур I: (3)

контур II: (4)

Получив систему уравнений относительно напряжений и токов (1)-(4), преобразуем ее к системе уравнений относительно новых функций: - заряд конденсатора и- потокосцепление катушки индуктивности.

Для этого следует исключить из нашей системы уравнение (1), так как оно содержит . Кроме того, из уравнений (2) и (4) следует исключить и . Так как , то

Тогда наша система сводится к двум уравнениям:

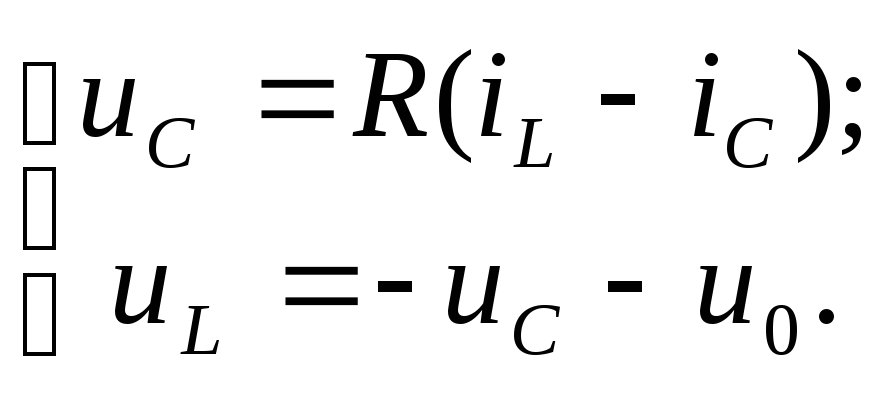
Поскольку ,,,, то

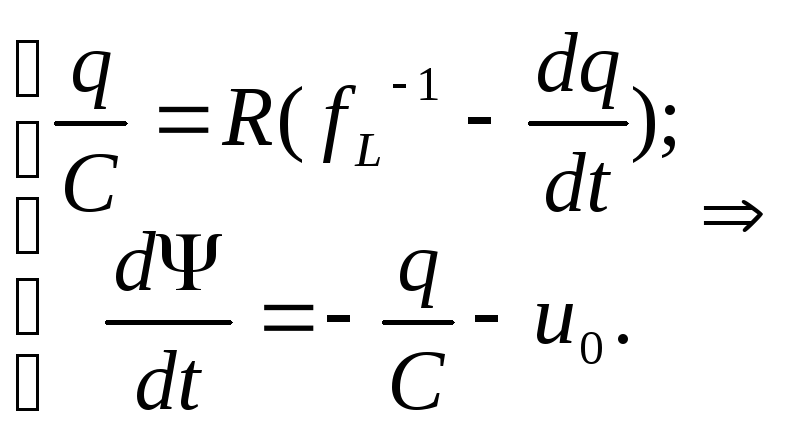
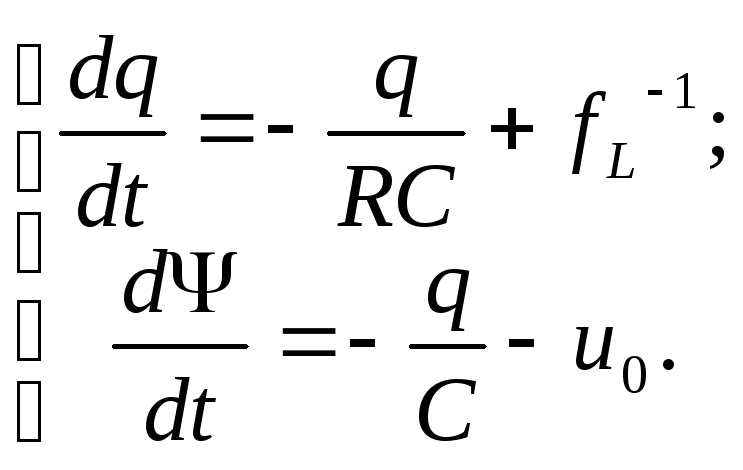(5)

Полученная система дифференциальных уравнений совпадает с приведенной в варианте.

2. Подставим заданные значения и зависимости в нашу систему. В результате она будет иметь следующий вид:

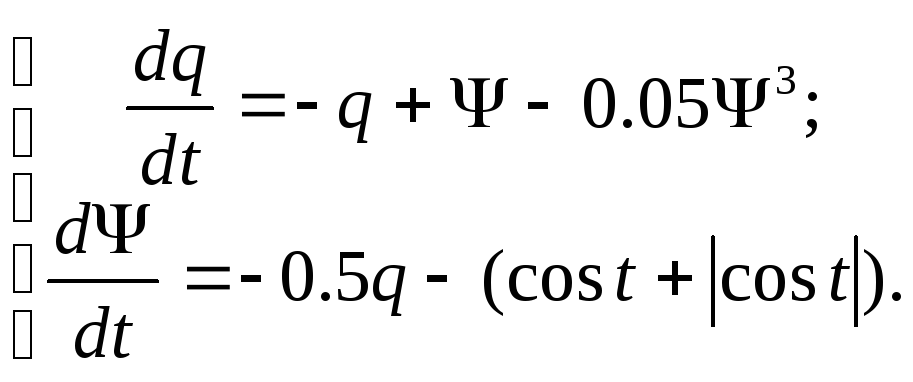(6)

Для вычисления значений ипо известнымивоспользуемся явной разностной схемой Рунге-Кутта для решения системы (6):

(7)

или

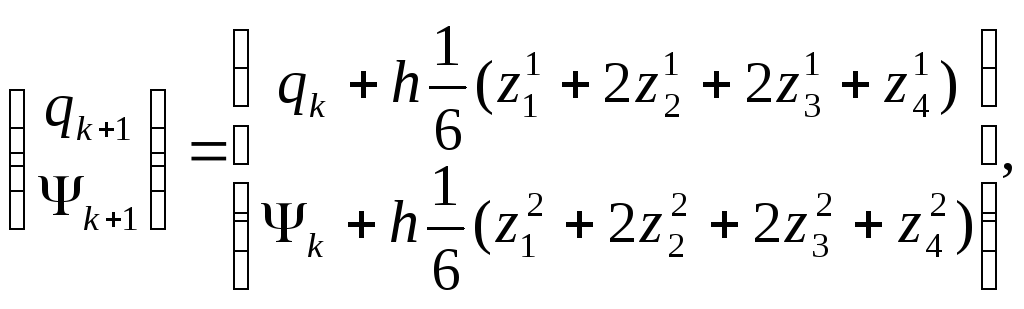(8)

где ,

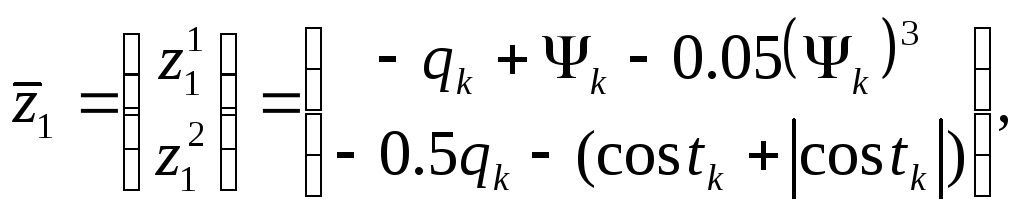
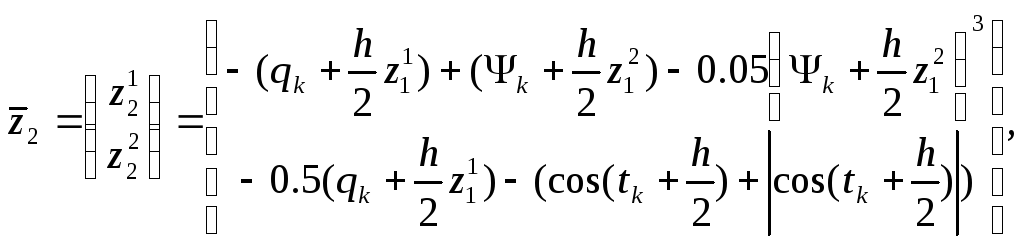
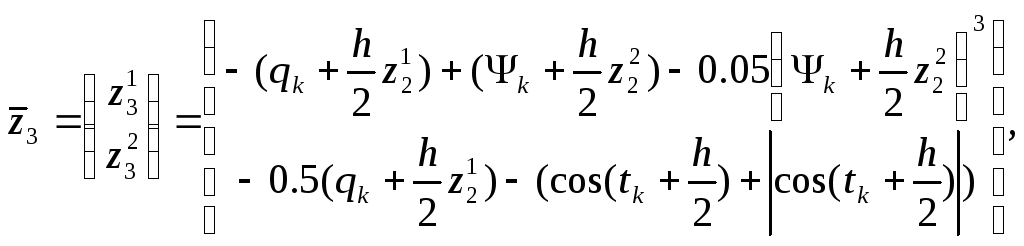
Составим разностную схему счета методом Гира 3-его порядка:

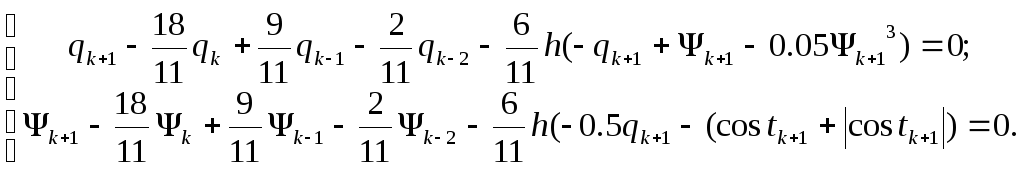(9)

или

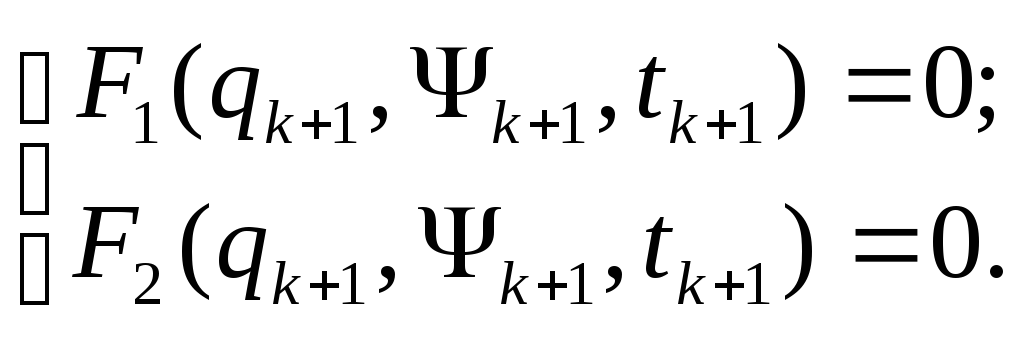
Расчет значений 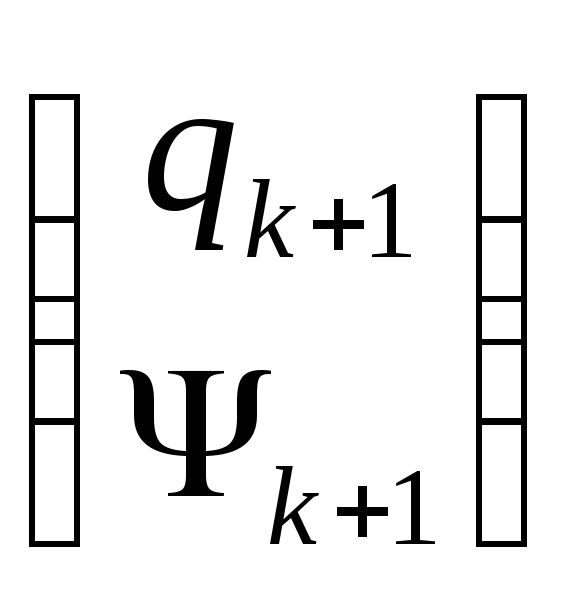проводим методом Ньютона-Рафсона:

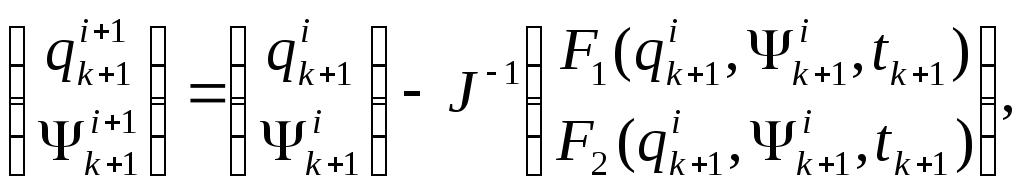(10)

где -матрица Якоби:

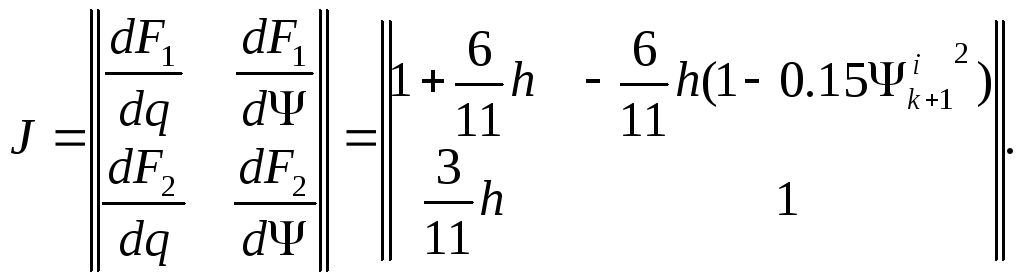(11)

В приведенных формулах индекс , стоящий вверху у функцийи, обозначает номер коррекции в итерационном процессе Ньютона-Рафсона.

3. Расчет сведен в таблицу 1, графики функций приведены на рис. 3 – 5. Расчет был произведен с помощью программного обеспечения исполнителя на ЭВМ типаIBMPCAT. Текст программы на языке С++ представлен в приложении 1. Визуализация численного решения была проведена с помощью программного комплексаMatlab5.2.

Таблица 1.

k = 0

t = 0 q = 1 psi = 1

k = 1

t = 0.5 q = 0.737822 psi = -0.185492

k = 2

t = 1 q = 0.18758 psi = -1.02806

k = 3

t = 1.5 q = -0.351542 psi = -1.33934

k = 4

t = 2 q = -0.719961 psi = -1.28606

k = 5

t = 2.5 q = -0.889783 psi = -1.07422

k = 6

t = 3 q = -0.902367 psi = -0.82605

k = 7

t = 3.5 q = -0.816343 psi = -0.595322

k = 8

t = 4 q = -0.681766 psi = -0.400648

k = 9

t = 4.5 q = -0.53323 psi = -0.246002

k = 10

t = 5 q = -0.423684 psi = -0.279936

k = 11

t = 5.5 q = -0.437009 psi = -0.656603

k = 12

t = 6 q = -0.625248 psi = -1.3286

k = 13

t = 6.5 q = -0.933755 psi = -2.0931

k = 14

t = 7 q = -1.22869 psi = -2.70109

k = 15

t = 7.5 q = -1.42629 psi = -2.94358

k = 16

t = 8 q = -1.54295 psi = -2.77694

k = 17

t = 8.5 q = -1.6088 psi = -2.40742

k = 18

t = 9 q = -1.62156 psi = -1.98146

k = 19

t = 9.5 q = -1.56523 psi = -1.56413

k = 20

t = 10 q = -1.43514 psi = -1.18031

k = 21

t = 10.5 q = -1.24468 psi = -0.842202

k = 22

t = 11 q = -1.01949 psi = -0.560225

k = 23

t = 11.5 q = -0.840147 psi = -0.591314

k = 24

t = 12 q = -0.808443 psi = -1.01241

k = 25

t = 12.5 q = -0.955243 psi = -1.68872

k = 26

t = 13 q = -1.19386 psi = -2.3747

k = 27

t = 13.5 q = -1.40031 psi = -2.82183

k = 28

t = 14 q = -1.53225 psi = -2.84728

k = 29

t = 14.5 q = -1.60921 psi = -2.56274

k = 30

t = 15 q = -1.63848 psi = -2.15361

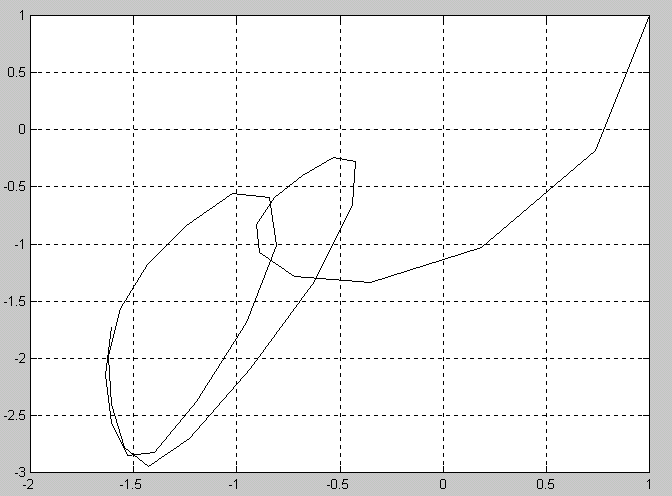
Рис. 3. Результаты численного решения системы (6) .

Рис. 4. График функции.

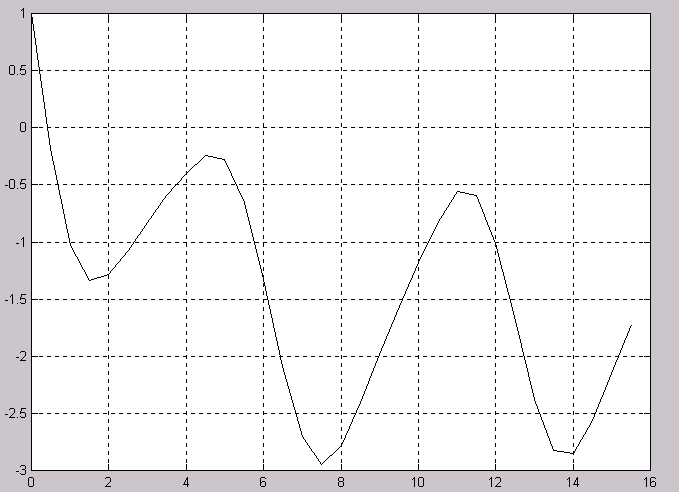
Рис. 5. График функции.