Информатика на Maple / лаб-р / Лаб 8

Лабораторная работа 8

Элементы комбинаторики. Вероятность

Алгебра событий

Множество всеx возможных исходов какого либо опыта, в котором заранее ничего нельзя сказать о появлении того или иного события, назовем пространством элементарных событий.

Любое подмножество пространства элементарных событий назовем случайным событием.

Класс подмножеств U пространства элементарных событий называется алгеброй событий, если U замкнуто относительно операций взятия суммы (объединения), разности, произведения (пересечения) случайных событий из U, U содержит пустое множество и само пространство элементарных событий .

Полной группой событий назовем множество событий таких,что

1. Объединение этих событий есть событие достоверное;

2. Любые два события группы попарно несовместны;

3.Невозможное событие также принадлежит этому множеству.

Вероятностью события А из полной группы событий назовем число Р(А) раное отношению числа событий, благоприятствующих появлению события А к полному числу событий полной группы.

Зададим пространство элементарных событий

> Omega:=[a,b,c,d];

Для построения алгебры событий U нам потребуется команда choose из библиотеки combinat

> ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set

U:=combinat[choose](Omega);

Вычислим количество n элементов в алгебре событий U

> n:=combinat[numbcomb](Omega);

Выполнение команды

> n:='n':

выгружает из памяти значение n (см. также команды forget, restart).

Контрольное задание.

Задача 1. Постройте пространство элементарных событий , алгебру событий и найдите количество элементов в алгебре событий:

а) для опыта с бросанием монеты один раз;

б) для опыта с бросанием игральной кости один раз;

в) для опыта с бросанием двух монет один раз;

г) для опыта с бросанием монеты два раза.

>

Контрольное задание.

Задача 2.

Производится опыт с бросанием монеты. Пространство элементарных событий множество

> moneta:=[o,p];

Это множество образует полную группу, события несовместны и равновозможны(да,да,да).

Составить пространства элементарных событий и определить

1.Образуют ли они полную группу;

2.Являются ли несовместными;

3.Являются ли равновозможными

в следующих опытах:

Опыт -одновременное бросание двух монет.

Опыт- последовательное бросание двух монет.

Опыт- выстрел по мишени

>

Подсчет числа комбинаций при появлении событий.

Для подсчета числа комбинаций при появлении событий из пространства элементарных событий применяются перестановки, размещения , сочетания без повторений и с повторениями.

Перестановки без повторений это такие комбинации из n различных элементов, которые отличаются друг от друга порядком следования.

Получим всевозможные перестановки из 4 цифр 1,2,3,4:

> P:=combinat[permute](4);

Найдем количество всевозможных перестановок из 4 элементов

> combinat[numbperm](4);

К примеру, в случайном порядке выписывают элементы a, b, c, d. Требуется найти вероятность того, что символы a и b окажутся рядом. Получим всевозможные перестановки из a, b, c, d:

> P:=combinat[permute]([a,b,c,d]);combinat[numbperm](4);

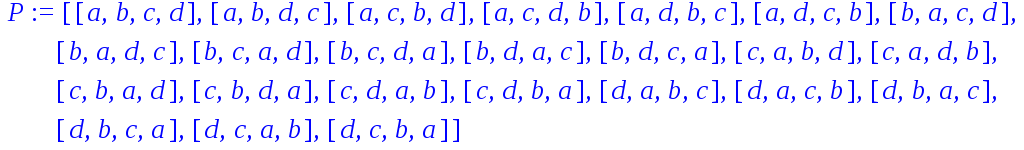
Всего перестановок из 4-х элементов 24.

Сгенерируем перестановки из элементов a,b,c,d так, чтобы элементы а, b были рядом

> Pab:=combinat[permute]([ab,c,d]);combinat[numbperm](3);

Всего элементов 6. С учетом перестановки символов a и b всего перестановок, благоприятствующих наступлению события "элементы a и b расположены рядом", будет 12. Тогда искомая вероятность равна .

Контрольное задание.

Задача 3. (Чистяков В. П. Курс теории вероятностей: Учеб.-3-е изд., испр.-М.: Наука. Гл. ред. физ.-мат. лит.- 1987.). На полке в случайном порядке расставлено n книг, среди которых находится двухтомник Д. Лондона. Предполагая, что различные расположения чисел равновероятны, найти вероятность того, что оба тома двухтомника расположены рядом.

Размещения из n элементов по m элементам без повторений это такие комбинации по m элементам в каждой, которые отличаются друг от друга или составом, или порядком следования элементов. Формула для их вычисления имеет вид

Вычислим количество размещений из 4 элементов по 2:

> combinat[numbperm](4, 2);

Составим размещения из элементов a, b, c, d по 2:

> combinat[permute]([a,b,c,d],2);

Контрольное задание.

Задача 4.

Сколько различных трехзначных чисел можно составить из 5 цифр 1,2,3,4,5.

>

Биномиальные коэффициенты, числа сочетаний. Сочетания без повторений из n элементов по m элементам это такие комбинации по m элементов в каждой, которые отличаются друг от друга составом элементов.

Формула для их вычисления имеет вид

Приведем примеры вычисления биномиальных коэффициентов (числа сочетаний)

> restart;binomial(5, 2);

> binomial(5, 3);

> binomial(6, 4);

Вычислим число сочетаний из n по 2 (по 3) и представим в виде произведения

> binomial(n, 2);

> factor(expand(%));

> binomial(n, 3);

> factor(expand(%));

Выразим число сочетаний из n по m через факториалы

> convert(binomial(n,m),factorial);

Контрольное задание.

Задача 5.

Сколькими способами можно из группы курсантов в 25 человек набрать погруппы для патрулирования улиц по 3 человека в каждой.

>

Перестановки с повторениями это такие комбинации из n элементов,отличающиеся друг от друга порядком следования элементов, среди которых могут быть одинаковые элементы.

Формула для их вычисления имеет вид

> restart:with(combinat, multinomial); multinomial(n, n2, n3,nk);

> P:=convert(multinomial(n, n2, n3,nk),factorial);

>

Размещения из n элементов по m элементам c повторениями это такие комбинации по m элементам в каждой, которые отличаются друг от друга или составом, или порядком следования элементов, среди которых могут быть одинаковые элементы. Формула для их вычисления имеет вид

> A[n^m]:=n^m;

Биномиальные коэффициенты, числа сочетаний с повторениями. Сочетания с повторениями из n элементов по m элементам это такие комбинации по m элементов в каждой, которые отличаются друг от друга составом элементов, причем среди элементов могут быть одинаковые.

Формула для их вычисления имеет вид

Выразим число сочетаний c повторениямииз n по m через факториалы

> C[(n+m-1)^m]:=convert(binomial(n+m-1,m),factorial);

Задача 6 .

Сколько можно составить семизначных чисел, состоящих из цифр 4,5,6, в которых цифра 4 повторяется 3 раза, 5-2 раза и 6 - 2 раза. Так как порядок следования цифр в числе важен и цифры могут повторяться, то имеем перестановки с повторениями и 7 элементов. Вычислим их число.

> restart;convert(multinomial(7, 3, 2,2),factorial);

Сколько можно составить различных семизначных чисел, состоящих из цифр 4,5,6, если среди цифр числа могут быть одинаковые. Так как порядок следования цифр важен, но все цифры числа могут быть одинаковыми, то имеем размещения с повторениями, так как цифр для составления числа 3 , а само число семизначное. Найдем число размещений с повторениями.

> restart;n:=3;m:=7;A[n]:=n^m;

В оранжерее имеются цветы 8 наименований.Сколькими способами можно составить букет из пяти цветов.

Так как порядок следования цветов в букете не важен, и букет может состоять из цветов одного наименования, то имеем сочетания с повторениями. Найдем число этих сочетаний.

> restart;n:=8;m:=5;C[(N+M-1)^M]:=binomial(n+m-1,m);

>

>

Контрольное задание.

Задача 7.

1.Сколько можно составить слов, состоящих из 3 букв А, 2 букв Н и одной буквы С.Порядок букв в слове важен.

2.Сколькими способами можно распределить 25 человек по 4 аудиториям, если в каждую аудиторию может поместиться все 25 человек.

3.Сколькими способами можно составить для украшения стола вазы с фруктами 6 наименований(яблоки, груши,сливы, апельсины,мандарины, абрикосы) по 4 фрукта в вазе.