2.3. Суперпозиция электростатических полей

При рассмотрении электростатического поля произвольной системы неподвижных точечных зарядов было экспериментально показано, что результирующая сила, действующая на пробный зарядq в любой точке поля, равна геометрической сумме сил, действующих на заряд q со стороны каждого из зарядов :

. (1.8)

Из (1.8) легко получить, что

. (1.9)

Последнее соотношение выражает принцип суперпозиции электрических полей (принцип независимости действия электрических полей): напряженность электрического поля, созданного системой зарядов в любой точке пространства, равна векторной сумме напряженности полей, созданных каждым зарядом в отдельности в этой точке.

Рассмотрим применение этого принципа для расчета напряженности поля системы дискретно и непрерывно распределенных зарядов.

3. Работа сил электростатического поля.

Разность потенциалов. Потенциал

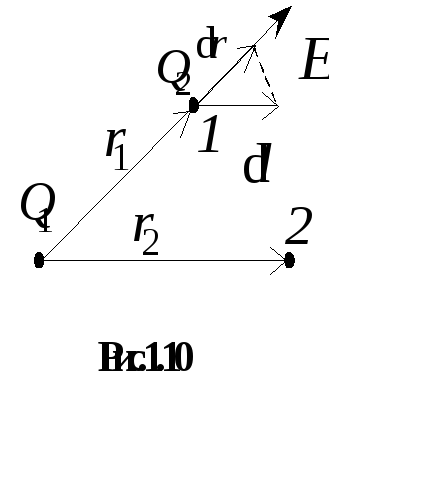
Электрическое поле точечного заряда является центральным, а поэтому потенциальным (см. часть I, п.3.2 ). Определим работу поля, созданного зарядом , по перемещению точечного зарядаиз точки1 в точку 2 (рис.1.10). Элементарная работа поля по перемещению заряда на расстояние равна

.

Тогда

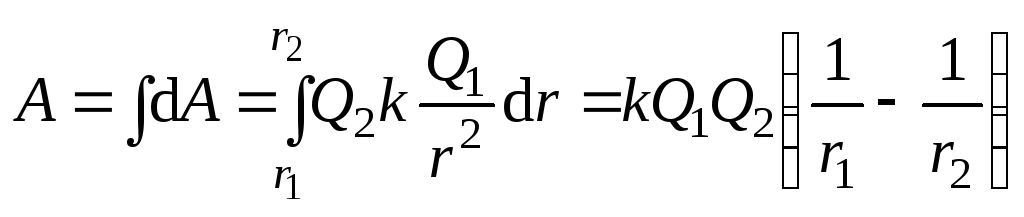. (1.10)

Если заряды одноименны, то поле совершает положительную работу при их удалении друг от друга и отрицательную работу при их сближении.

Из (1.10) видно, что работа сил электростатического поля по перемещению заряда не зависит от формы траектории движения заряда, а определяется положением начальной и конечной точек траектории. Итак, кулоновские силы потенциальны. Для таких сил , а поэтомуциркуляция напряженности электростатического поля по произвольному замкнутому контуру равна нулю:

. (1.11)

Условие (1.11) является необходимым и достаточным для того, чтобы электростатическое поле было потенциальным. Тогда справедлива связь работы потенциальной силы и изменения потенциальной энергии:

. (1.12)

Рассмотрим отношение работы поля по перемещению пробного заряда из одной точки пространства в другую к величине переносимого заряда:

.

Поскольку полученное отношение не зависит от переносимого заряда и траектории его перемещения, то данная величина может быть принята в качестве характеристики рассматриваемого поля. Разностью потенциалов между двумя точками электростатического поля называется отношение работы сил поля по перемещению пробного электрического заряда из одной точки в другую к величине этого заряда:

. (1.13)

Если использовать (1.12), то можно получить, что

.

Из данного соотношения будет следовать, что

, (1.14)

т.е. потенциал электростатического поля равен отношению потенциальной энергии пробного электрического заряда, помещенного в данную точку поля, к величине заряда. Ранее мы отмечали, что потенциальная энергия – величина, не имеющая физического смысла, поскольку определена с точностью до некоторого произвольного постоянного значения. Поэтому и потенциал тоже лишен физического смысла, в любой точке пространства можно условно принять его значение как нулевое. Воспользуемся (1.12) и примем . Тогда

. (1.15)

Таким образом, потенциал любой точки электростатического поля численно равен работе, совершаемой силами поля при перемещении единичного положительного заряда из этой точки в ту, где потенциал поля условно принят равным нулю. Выбор точки с нулевым потенциалом произволен и определяется удобством решения каждой конкретной задачи. Рассмотрим это на некоторых примерах.

Пример 1. Определим потенциал произвольной точки пространства, удаленной на расстояние r от точечного заряда Q (рис. 1.11). В соответствии с (1.15) выберем точку, где . Пусть это будет точка, бесконечно удаленная от зарядаQ. Поскольку величина работы по переносу пробного заряда из исследуемой точки в бесконечность не зависит от формы траектории движения, то рассмотрим такое движение пробного заряда, при котором (т.е. по прямой). Тогда

.

Мы получили формулу зависимости потенциала поля точечного заряда от расстояния до него. На рис. 1.12 показан график функции (r).

Пример 2. Рассмотрим электростатическое поле, создаваемое системой точечных зарядов . Тогда потенциал произвольной точки пространства можно определить как, где– вектор напряженности поля, найденный по принципу суперпозиции (1.9):

,

. (1.16)

Таким образом, потенциал поля системы точечных зарядов равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности. В этом состоит принцип суперпозиции потенциала электростатического поля.

При рассмотрении поля, созданного непрерывно распределенным зарядом, необходимо выполнить следующую последовательность действий:

1. Выделить в объекте точечный элемент с зарядом .

2. Выразить потенциал поля этого заряда в рассматриваемой точке.

3. Определить потенциал в заданной точке пространства согласно принципу суперпозиции.