Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Основы технологии электронной компонентной базы / материалы по технологии / Конспект лекций.pdf

Скачиваний:

1893

Добавлен:

31.03.2015

Размер:

9.88 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 6318 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

величину коэффициента диффузии, при этом обычно несколько уменьшается

ивеличина E .

4.Атмосфера, в которой ведется диффузия примеси. Для Si, наиболее сильно проявляется влияние кислорода. Кислород относится к числу быстродиффундирующих примесей и ускоряет диффузию ряда других примесей. Его роль будет рассмотрена позже.

5.Механические напряжения и сопутствующая им повышенная концентрация дислокаций. Вдоль дислокаций диффузия примеси идет во много раз быстрее, чем в бездефектном материале.

6.Ориентация кристалла. То, что этот фактор должен работать в случае неизотропных кристаллов, представляется достаточно очевидным. Однако его влияние проявляется и в таких кристаллах, как Ge и Si. В данном

случае может сказываться роль дислокаций, имеющих некоторые предпочтительные направления в алмазоподобных решетках, и кислорода, всегда имеющегося в качестве фоновой примеси и также имеющего определенные предпочтительные конфигурации кластеров, в виде которых он преимущественно и находится в решетке Si. Этот аспект также будет рассматриваться позже.

Взаключение этого раздела нужно заметить, что в большинстве учебных пособий справочные данные по коэффициентам диффузии обычно приводятся без указания конкретных условий, при которых проводились соответствующие эксперименты. Для одной и той же примеси данные разных источников могут различаться в несколько раз. Наиболее корректные данные по диффузии примесей в Si, по-видимому, приведены в двухтомнике С. Зи Технология СБИС.

Взаключении следует упомянуть о параметре, широко обсуждаемом в литературе, посвященной ионному легированию полупроводников, а именно,

окоэффициенте активности примеси. Мерой коэффициента активности является отношение числа доноров (или акцепторов) к общему числу находящихся в материале атомов соответствующей примеси. При диффузионном легировании коэффициент активности примеси обычно практически равен единице. Меньшие значения коэффициента активности обычно наблюдаются при концентрациях, близких к предельной растворимости. В данном случае, скорее всего, сказывается образование групп из нескольких соседствующих атомов, часть которых не является активными. Кроме того, примеси могут захватываться на разного типа дефекты и также становиться неактивными.

6.3. Моделирование процессов диффузии в твердом теле

При высокой концентрации примеси, как в случае диффузии в условиях постоянной поверхностной концентрации, так и в случае диффузии из ограниченного источника, измеряемые профили распределения концентрации примеси отклоняются от рассчитанных согласно уравнениям (6.13). В большинстве случаев профиль распределения примеси в областях с высокой концентрацией может быть описан с помощью концентрационной

зависимости коэффициента диффузии. Для определения концентрационной зависимости коэффициента диффузии из экспериментальных данных используют уравнение (6.5).

В этом раз деле, как и в предыдущем, процесс диффузии рассматривается при двух условиях: постоянной поверхностной концентрации диффузанта и постоянном общем числе атомов диффузанта.

Постоянная поверхностная концентрация. Уравнение (6.5)

N x, t			N x, t	(6.5)
t		D	x

	x

представляет собой одномерное уравнение диффузии с коэффициентом диффузии, зависящим от концентрации диффузанта. В тех случаях, когда D зависит только от концентрации диффузанта N и поверхностная концентрация поддерживается на постоянном уровне, уравнение (6.5) может быть преобразованно в обычное дифференциальное уравнение с новой переменной

Тогда z 1 , z

x t t

Подставляем x и

z	x

		t

, отсюда x

t z и t

z .

t во второй закон Фика (6.5):

N x, t

t z

N x, t

t z

N x, t

(6.15)

(6.16)

Таким образом, как D, так и N зависят явным образом только от x. Решения уравнений с новыми переменными в рассматриваемых ранее

случаях будут выглядеть следующим образом.

6.3.1. Диффузия из одной полуограниченной области в другую

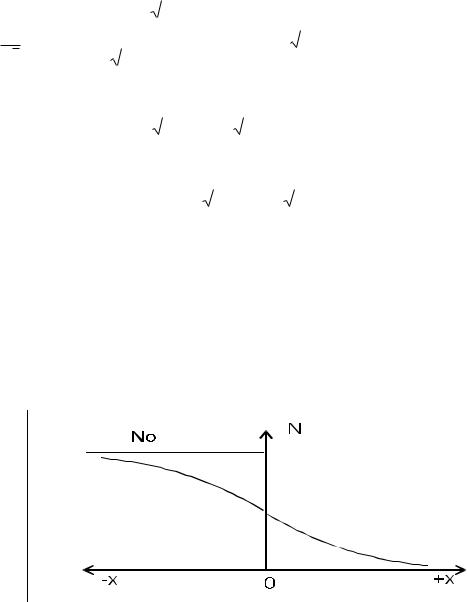
Пусть Распределение примеси имеет следующий вид (рис. 6.3):

Рис. 6.3.

Распределение примеси при диффузии из одной полуограниченной области в другую

Краевые условия для этого случая записываются в следующем виде:

N ,t N N0 const

N , t N 0

Начальные условия:
при t 0	и любых x 0		, z		x			, а N x,0 0 ;

						t
						t
при t 0	и любых x 0		, z , N x,0 N .
							0
Ход вычислений становится более прозрачным, если временно ввести
новую	переменную	F		d N .				Тогда (6.16) перепишется в форме,
		F		d z

соответствующей уравнению с разделяющимися переменными.

F ,

которое можно записать в виде:

Интеграл этого выражения равен

ln F

или

C2 exp

(6.17)

(6.18)

(6.19)

(6.20)

Здесь C1 и C2 – это просто две разных записи для одной и той же постоянной интегрирования. Из (6.20) очередным интегрированием получается:

		z2		2
N z C2	exp		dz C3	C4 exp u	du C3	(6.21)

		4D

Произведена замена переменной u z2 4D ,
Произведена замена переменной u z2 4D ,				а множитель 2			D при C2
включен в состав постоянной интегрирования С4.
Оставшиеся постоянные интегрирования С3				и С4	нужно определять с
учетом начальных и краевых условий. Рассмотрим					значение	интеграла,
exp( u2 )du , вычисляемого в пределах от uo до + ∞.
Если u0 , z x		и N z N 0 , и, следовательно,
Если u0 , z x	t	и N z N 0 , и, следовательно,
С3=0.
Если u0 , то
exp( u2 )du			, а N z N N0 .
exp( u2 )du			, а N z N N0 .			(6.22)

Следовательно, C4 N0 .

Таким образом:

N x,t

(6.23)

erfc

D t

В анализировавшемся нами примере область, первоначально не содержавшая примеси, соответствовала положительным значениям аргумента. Если бы она приходилась на его отрицательные значения, то имело бы место соотношение erfc u 1 erf u .

Важно отметить, что erfc 0 1, так что

N 0,t N20 const NS .

Таким образом, профиль распределения примеси при диффузии из

источника неограниченной мощности обычно записывают в форме

N x, t NS	x
	erfc		.	(6.24)

		L

6.3.2. Количество примеси, введенной из источника неограниченной мощности

Как уже отмечалось ранее, источник неограниченной мощности чаще всего используется на стадии “загонки” примеси. Для вычисления количества примеси в этом случае достаточно проинтегрировать (6.24) по всему пространству 0 x . Формальное вычисление этого интеграла оказывается достаточно длительным. Проще сначала вычислить зависящую от времени величину потока примеси через поверхность x 0 , и затем проинтегрировать по всему времени “загонки”.

Исходя из (6.4) и (6.5):

d N

; N x, t

N x, t

j x,t D d N x,t D N S

exp u 2

d x

(6.25)

x L

D N

exp x2 L2

Соответственно,

j 0,t D N S

D N S

N S

(6.26)

D t

После интегрирования абсолютной величины потока примеси по t получим:


t	D t
Q j t dt 2NS		(6.27)


0

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 6318 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в папке материалы по технологии

#
31.03.20159.88 Mб1893Конспект лекций.pdf
#
31.03.20152.78 Mб394Методы выращивания кристаллов.doc
#
31.03.2015431.62 Кб178ПП материалы.doc
#
31.03.20151.11 Mб193Смирнов.pdf
#
31.03.20152.43 Mб363Технология 2.doc