Лаб_РСПИ_No4

2

2. отображение каждой k-битовой информационной последовательности во вза-

имно однозначную n-битовую последовательность, называемую кодовым сло-

вом.

Рис. 1.1. Обобщенная схема цифровой системы связи

Число избыточных (проверочных) битов равно r (r = n – k). Избыточность

двоичного кода определяется отношением [1] χ (χ = r/n = 1 – k/n), где величина k/n называется скоростью кодирования или кодовой скоростью.

Двоичная последовательность с выхода кодера поступает на модулятор,

который в соответствии с его назначением отображает один или несколько дво-

ичных символов с выхода кодера канала в конкретный узкополосный сигнал.

При использовании двоичной модуляции можно считать, что логический «0»

отображается узкополосным сигналом s1(t), а логическая «1» отображается уз-

кополосным сигналом s2(t), каждый сигнал длительностью τдв. При использова-

нии многоуровневой модуляции блоку из q битов ставится в соответствие один из M = 2q узкополосных сигналов si(t), i = 1, …, M. Каждый сигнал si(t) имеет длительность Тс.

На приемной стороне цифровой системы связи демодулятор обрабатывает сигналы, искаженные шумом и помехами, и преобразует каждый принятый сигнал в скаляр или вектор, который является оценкой переданных двоичных или М-позиционных символов. Решающее устройство на выходе демодулятора формирует одно из Q решений относительно переданного символа.

4

Решающее устройство может работать по жесткой или мягкой схеме. Ес-

ли говорят о жестком решении (hard decision) демодулятора, то М = 2 и фор-

мируется одно из двух решений «0» или «1». Если используются М-позицион-

ные сигналы (М > 2), то Q = M.

В общем случае на выходе решающего устройства формируется много-

уровневое решение, при этом значение Q можно рассматривать как число уров-

ней квантования. Если используются М-позиционные сигналы, то число реше-

ний Q > M. В этом случае говорят о мягком решении (soft decision) демодуля-

тора. Заметим, что возможна ситуация, когда вообще не производится кванто-

вание сигнала на выходе демодулятора, при этом Q = .

Квантованный выходной сигнал демодулятора подается на канальный де-

кодер, где происходит коррекция внесенных каналом искажений в демодулиро-

ванные данные с использованием избыточности кода.

1. Модели и пропускная способность каналов связи

В лабораторной работе рассматривается модель дискретного канала, кото-

рая используется при анализе систем связи с кодированием, для входа и выхода которых характерно наличие дискретных по уровню сигналов. В общем случае модель дискретного канала содержит набор множества возможных сигналов на его входе и выходе, а также набор значений условных вероятностей появления выходного сигнала при заданном входном.

Наиболее простой является модель двоичного симметричного канала

(ДСК, binary symmetric channel – BSC), которая соответствует случаю M = Q =

2, то есть использованию двоичного сигнала и жесткого решения демодулятора.

Модель двоичного симметричного канала

Пусть на выходе кодера канала (рис. 1.1) формируется последовательность двоичных символов 0 и 1. Этот двоичный цифровой сигнал преобразуется в по-

следовательность электрических сигналов и поступает на модулятор, сигнал с

5

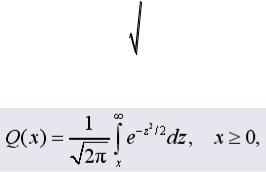
выхода модулятора (или передающей части системы связи) передается по не-

прерывному (например, гауссовскому) каналу на приемное устройство, где принятая смесь сигнала и шума демодулируется. При работе демодулятора по жесткой схеме на его выходе формируется последовательность двоичных сим-

волов 0 и 1. Обозначим этот сигнал mд(t). В общем случае при наличии шума в канале последовательность на входе модулятора передатчика m(t) отличается от последовательности на выходе демодулятора приемника mд(t). Отличие этих двух сигналов или последовательностей двоичных символов вызвано искаже-

нием сигнала в дискретном канале связи, состоящем из модулятора, канала с шумом и демодулятора.

Рассматриваемый канал имеет на входе символы U = {0, 1}, на выходе символы Z = {0, 1}. Также характеристикой этого канала является набор услов-

ных вероятностей возможных выходных символов от возможных входных:

Если канальный шум и помехи вызывают в канале статистически незави-

симые ошибки при демодуляции двоичной последовательности со средней ве-

роятностью ошибки р, то условные вероятности (1.1) определяются так:

где, например, в случае передачи данных сигналами ФМ2 средняя вероятность ошибки определяется по формуле:

где

(1.4)

Q(x) – дополнительный интеграл вероятности,

6

– отношение энергии двоичного сигнала к односторонней спектраль-

ной плотности шума на входе приемника.

Выражения (1.1) и (1.2) определяют так называемые вероятности перехода.

Иными словами, при передаче канального символа вероятность принятия его с ошибкой равна р, а вероятность того, что он принят без ошибки, равна (1 – р).

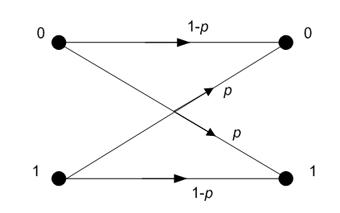
Переходы входных символов в выходные в соответствие с соотношениями (1.1)

могут быть описаны графом на рис. 1.2. Эту модель симметричного канала с двоичным входом и двоичным выходом обычно называют двоичным симмет-

ричным каналом. Поскольку каждый выходной двоичный символ зависит только от соответствующего входного двоичного символа и не зависит от пре-

дыдущих и последующих символов, такой канал называют каналом без памя-

ти.

Рис. 1.2. Модель ДСК

В ДСК декодер работает на основе жестких решений на выходе демодуля-

тора, поэтому декодирование в двоичном симметричном канале является жест-

ким.

Дискретный канал без памяти

ДСК является частным случаем более общей модели дискретного канала.

Пусть на входе канала имеются q-ичные символы U = {u1, u2, ..., uq}, на вы-

ходе решающего устройства Q-ичные символы Z = {z1, z2, ..., zQ }, где Q M = 2q. Если канал и модуляция без памяти, то характеристикой канала является на-

бор условных вероятностей

7

Такой канал называется дискретным каналом без памяти (ДКБП, discrete memoryless channel – DMC). Графическая модель такого канала изобра-

жена на рис. 1.3.

Рис. 1.3. Модель дискретного канала без памяти

Каждый выходной символ канала зависит только от соответствующего входного символа. Поэтому для данной реализации последовательности симво-

лов входного алфавита {u1, u2, u3, ..., un} и реализации соответствующей после-

довательности символов выходного алфавита {z1, z2, z3, ..., zn} совместная ус-

ловная вероятность определяется следующим образом:

(1.6)

Если же канал имеет память (т.е. сигнал в канале подвергается замирани-

ям), совместную условную вероятность последовательности нужно выражать как совместную вероятность всех элементов последовательности. Выражение

(1.6) – это условие отсутствия памяти в канале. Поскольку считается, что шум в канале без памяти влияет на каждый символ независимо от других, то в этом случае условная вероятность появления реализации последовательности {z1, z2, z3, ..., zn} является произведением вероятностей независимых элементов.

Непрерывный канал

8

независимы и некоррелированы. Следовательно, переходные вероятности оп-

ределяются как произведение независимых условных вероятностей для каждого i:

(1.11)

для любого значения N. Таким образом, модель непрерывного канала – это ка-

нал с дискретным временем и совместными переходными вероятностями (1.11).

Пропускная способность дискретного канала без памяти

Рассмотрим дискретный канал без памяти со входным алфавитом U = {u1, u2, ..., uq}, выходным алфавитом Z = {z1, z2, ..., zQ} и набором переходных веро-

ятностей

(1.12)

Предположим, что передан символ uj, а принят символ zi. Взаимная информа-

ция о событии U = uj, когда имеет место событие Z = zi, равно log[P(zi|ui)/P(zi)],

где

(1.13)

Следовательно, средняя взаимная информация, получаемая по выходу Z о вхо-

де U, равна [4]

(1.14)

Характеристики канала определяются переходными вероятностями P(zi|uj),

и вероятности входных символов определяются дискретным кодером канала.

Величина средней взаимной информации I(U; Z), максимизируемая по набору вероятностей входных символов, зависит только от характеристик двоичного канала без памяти через условные вероятности P(zi|uj). Эта величина называется пропускной способностью канала и обозначается С0.

10

Пропускная способность дискретного канала без памяти определяется

как

(1.15)

Вычисление максимума величины средней взаимной информации I(U; Z)

выполняется при следующих условиях:

(1.16)

Величина С0 имеет размерность бит/символ, при этом основание логариф-

ма в (1.15) равно 2.

На основе соотношений (1.15) и (1.16) можно записать выражение для пропускной способности двоичного симметричного канала.

Для ДСК с переходными вероятностями P(0/1) = P(1/0) = p пропускная способность канала определяется по формуле

11