
Лаб_РСПИ_No4
.pdfПри р = 0 и р = 1 средняя взаимная информация между входом и выходом канала равна 1, то есть в информации о входной последовательности символов содержится полная информация о выходной последовательности и обратно.
Поэтому пропускная способность канала в этих граничных случаях максималь-
на и равна 1 бит/символ.
При P(0/1) = P(1/0) = 1/2 средняя взаимная информация минимальна и рав-
на 0. Следовательно, пропускная способность канала равна 0. При увеличении средней вероятности ошибки р от 0 до 1/2 пропускная способность падает от 1
бит/символ до 0; при дальнейшем росте величины р пропускная способность возрастает до 1 бит/символ. Зависимость пропускной способности ДСК от ве-
роятности ошибки р является четной функцией относительно точки р = 1/2.
Читателю известно, что величина р является монотонно убывающей функ-
цией от величины отношения сигнал/шум, что следует, например, из формулы
(1.2). Величина средней вероятности ошибки не превосходит значение 1/2, по-
этому может рассматриваться лишь левая половина графика на рис. 1.3. Из этих соображений очевидно, что при увеличении отношения сигнал/шум от 0 до пропускная способность ДСК возрастает от 0 и стремится к 1.
Наибольший интерес для практических задач представляют каналы связи со средней вероятностью ошибки на выходе демодулятора, не превосходящей
0,1.
Если скорость поступления двоичных символов на вход канала 1/Tc, то
пропускная способность С канала в единицу времени (в секунду) равна C/Tc и
измеряется в бит/с.
Пропускная способность непрерывного канала
Рассмотрим ограниченный по полосе частот канал с аддитивным белым гауссовским шумом (АБГШ). Формально пропускная способность такого кана-
ла в секунду определена К. Шенноном как [4]:
12
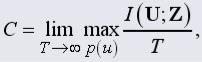
(1.18)
где средняя взаимная информация, получаемая по выходу Z о входе U, равна
|
|
|
P z | u |
|
|
|
I U; Z |
|
p(u) p z | u log |
du dz |
(1.19) |
||
|
||||||
|
|
p z |
|
|||
|
|
|
|
|||
В последнем выражении приняты следующие обозначения: U, Z – случай-
ные процессы с функциями плотности вероятности p(u), p(z) соответственно; p(z|u) – условная плотность вероятности процессов u(t) и z(t).
Основная формула для расчета пропускной способности в единицу време-
ни (предельной скорости передачи информации) частотно-ограниченного кана-
ла с АБГШ при ограниченном по полосе и средней мощности входном сигнале имеет вид:
|
|
|
P |
|
|
C W log2 |
1 |
|
ср |
|
(1.20) |
|
|||||
|
|
|
WN0 |
|
|
где C – предельная скорость передачи информации в непрерывном канале с АБГШ;
W – ширина полосы частот сигнала;
Рср – средняя мощность входного сигнала;
N0 – односторонняя спектральная плотность шума АБГШ.
Впервые эта формула получена в 1946 г. К. Шенноном. При желании чита-
тель может проследить вывод (1.20) по монографии [4, п. 7.1.2, с. 327].
Зависимость предельной скорости передачи информации в непрерывном частотно-ограниченном канале с АБГШ от отношения сигнал/шум построена на рис. 1.5.
Из (1.20) следует, что предельная скорость передачи увеличивается моно-
тонно при увеличении отношения сигнал/шум. Тогда при фиксированной поло-
се частот W предельная скорость передачи по каналу увеличивается при росте средней мощности переданного сигнала. Если же средняя мощность Рср зафик-
13
сирована, то предельную скорость передачи можно увеличить за счет расшире-
ния полосы частот W.
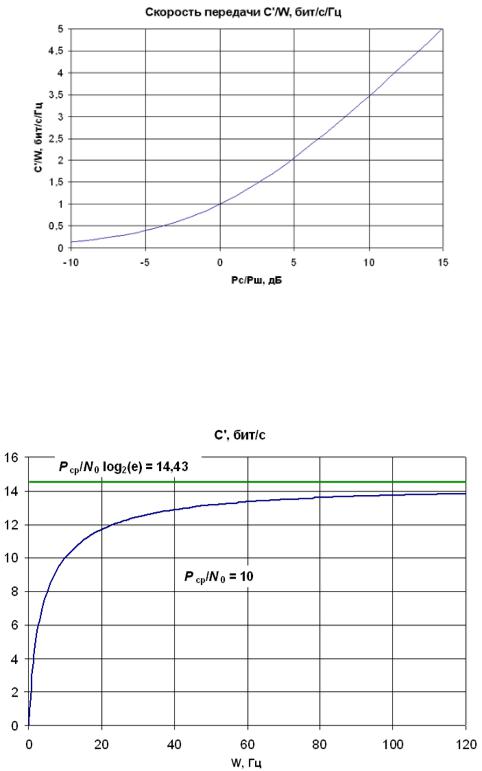
Рис. 1.5. Зависимость предельной скорости передачи информации в непрерывном
частотно-ограниченном канале с АБГШ от отношения сигнал/шум
Зависимость предельной скорости передачи в непрерывном частотно-
ограниченном канале с АБГШ от полосы частот W построена на рис. 1.6.
Рис. 1.6. Зависимость предельной скорости передачи информации в непрерывном
частотно-ограниченном канале с АБГШ от полосы W
14
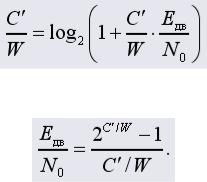
Можно показать, что при неограниченном росте полосы W предельная скорость передачи информации не превышает число Pср  N0 ln 2 . График на рис. 1.6 построен для отношения Pср
N0 ln 2 . График на рис. 1.6 построен для отношения Pср  N0 10 . Заметим, что при значении поло-
N0 10 . Заметим, что при значении поло-
сы W, численно равном Pср 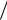 N0 10 Гц, предельная скорость передачи численно равна полосе W. Последнее можно непосредственно получить из формулы
N0 10 Гц, предельная скорость передачи численно равна полосе W. Последнее можно непосредственно получить из формулы
(1.20).
Из той же формулы (1.20) можно получить зависимость для нормирован-
ной к полосе предельной скорости передачи C/W в непрерывном канале от от-
ношения Едв/N0, где Едв – энергия сигнала, требуемая для передачи одного бита информации, N0 – односторонняя спектральная плотность АБГШ:
или
(1.21)
При неограниченном росте C/W (C/W ) отношение Едв/N0 возрастает по экспоненте. При C/W 0 отношение Едв/N0 = ln2 = –1,6 дБ.
Зависимость нормированной к полосе предельной скорости передачи C/W
в непрерывном канале от отношения Едв/N0 построена на рис. 1.7.
Кривая на рис. 1.9 делит всю плоскость характеристик сигналов на 2 об-
ласти. Ниже кривой (справа) расположена область, соответствующая фи-
зически реализуемым каналам связи. Выше кривой (слева) располагается об-
ласть, соответствующая физически нереализуемым каналам связи.
15
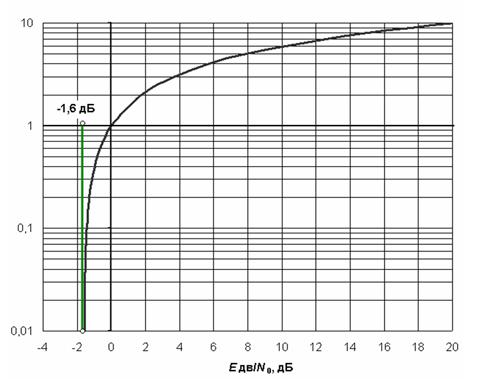
Рис. 1.7. Зависимость нормированной к полосе предельной скорости передачи C'/W в
непрерывном канале от отношения Едв/N0
Подведем итог. Главное значение приведенных формул для пропускной способности канала заключено в том, что они определяют верхнюю границу скорости передачи для реализуемой системы связи по каналу с шумом. Фунда-
ментальная роль, которую играет предельная пропускная способность канала,
определена теоремами кодирования в канале с шумами, сформулированными и доказанными К. Шенноном.
Теоремы кодирования для канала с шумом.
Существуют кодеры и декодеры канала такие, которые делают возможным достижение надежной связи с требуемой сколь угодно малой вероятностью ошибки, если реальная скорость передачи R меньше пропускной способности канала С, то есть при R < C.
Если R > C, то не существует процедуры кодирования и декодирования,
обеспечивающих требуемую сколь угодно малую вероятность ошибки при пе-
редаче информации.
16
2. Общие принципы помехоустойчивого кодирования и декодирования
Повышение требований к скорости и достоверности передачи данных,
увеличение протяженности линий связи, использование каналов с высоким уровнем помех, а также повышение плотности записи на носителях информа-
ции приводит к необходимости применения специальных мер, уменьшающих число ошибок при передаче и воспроизведении информации.
Канальное кодирование (channel coding) – это класс преобразований сигна-
ла, выполняемых для повышения качества связи или достоверности передачи данных. Теория помехоустойчивого кодирования позволяет выбрать наиболее эффективный метод обнаружения и исправления ошибок для каждого конкрет-
ного канала. Существуют два взаимно дополняющих метода борьбы с искаже-
ниями информационного потока:
кодирование для исправления ошибок – декодер приемника обнаружива-
ет и исправляет ошибки;
кодирование для обнаружения ошибок – приемник обнаруживает ошибки
ив случае необходимости производит запрос на повторную передачу искажен-
ного блока данных.
Последний метод предполагает наличие канала обратной связи и применя-
ется в каналах с малой вероятностью ошибки, если эту вероятность необходимо еще более понизить. Такая ситуация часто возникает в вычислительных сетях.
Типичное значение вероятности ошибки на бит без кодирования в вычисли-
тельных сетях составляет 10-6. Использование простейших кодов с небольшой избыточностью позволяет достигать значений 10-9 и ниже.
Рассмотрим радиотехнические системы, использующие цифровые сигналы для передачи данных радиотехническими методами по радиоканалу. Канальное кодирование можно считать способом приведения параметров такой системы к желаемым:
1. достижение заданной достоверности передачи при наименьшей ширине спектра радиосигнала;
17
2. нахождение компромисса между увеличением мощности сигнала и расши-
рением полосы пропускания канала связи для достижения заданной достовер-
ности передачи.
Идея использования канального кодирования заключается в следующем.
При постоянной информационной скорости за счет введения избыточности при кодировании повышается битовая скорость (укорачиваются импульсы на входе модулятора) и возрастает ширина спектра сигнала на выходе передатчика. По-
скольку при этом энергия одного электрического сигнала уменьшается (при по-
стоянной мощности сигнала и более коротком кодовом импульсе), то возраста-
ет вероятность ошибки р в канале. Однако если при декодировании исправляет-
ся значительная часть ошибок, то вероятность ошибки в переданном фрагменте данных уменьшается, и в этом случае применение кодирования оправдано.
Плюсы кодирования: кодирование понижает требуемое отношение сиг-
нал/шум в канале и дает энергетический выигрыш при фиксированной вероят-
ности ошибки.
Минусы кодирования: расширение полосы частот, занимаемой сигналом;
усложнение оборудования, увеличение времени обработки сигнала за счет де-
кодирования.
Выбор кода и алгоритма его декодирования, обеспечивающих заданный энергетический выигрыш при допустимом расширении полосы частот и приемлемой сложности, – одна из важнейших задач прикладной теории ко-
дирования.
Обычно представляется, что в канале связи к модулированному сигналу аддитивно добавляется шум. Предполагается, что шум и передаваемый сигнал независимы. Такой моделью можно пользоваться, если рассматривать каналы с аддитивным белым гауссовским шумом, каналы с релеевскими замираниями,
двоичный симметричный канал. На приемной стороне декодер канала исполь-
зует избыточные символы для исправления ошибок, внесенных каналом связи.
В режиме обнаружения ошибок декодер ведет себя как кодер полученного из
18

канала сообщения и проверяет совпадение вычисленных избыточных символов
спринятыми.
Внастоящее время специалистами в области теории информации и коди-
рования предложено много эффективных методов кодирования и декодирова-
ния, что позволило считать кодирование эффективным средством обеспечения высокой надежности передачи в современных цифровых системах связи. Для контроля ошибок целесообразно использовать коды с хорошей обнаруживаю-
щей и исправляющей способностью.
Радиоканал часто подвержен воздействию глубоких замираний, что вызы-
вает появление пакетов ошибок. Для борьбы с такого рода ошибками исполь-
зуют специальные коды, исправляющие серии ошибок, например, коды Рида-
Соломона и каскадное кодирование, а также перемежение кодированных сим-
волов.
3. Циклические коды БЧХ
Коды Боуза-Чоудхури-Хоквенгема (Bose-Chadhuri-Hocquenghem – ВСН,
БХЧ) относятся к классу циклических кодов. Коды БЧХ составляют класс ко-
дов, который обеспечивает достаточную свободу выбора длины блока, скоро-
сти кодирования, размера алфавита и возможностей коррекции ошибок. Коды БХЧ очень важны, поскольку при блоках, длина которых порядка несколько со-
тен, коды БХЧ превосходят своими качествами все другие блочные коды с той же длиной блока и скоростью кодирования. В наиболее часто применяемых ко-
дах БХЧ используется двоичный алфавит и кодовое слово длиной п = 2т – 1, где
т = 3, 4, ... . Примером недвоичных кодов БЧХ являются коды Рида-Соломона.
На рис. 3.1 и 3.2 изображены графики1 вероятности ошибки Рв для двух кодов БХЧ: (127, 64) и (127, 36). На рис. 3.1 показана зависимость Рв от вероят-
ности ошибки p в канальном символе при жестком декодировании. Полный анализ и сопоставление этих зависимостей студенту предлагается проделать
1 Графики, приведенные на рис. 3.1, 3.2, 3.3, опубликованы в [5].
19
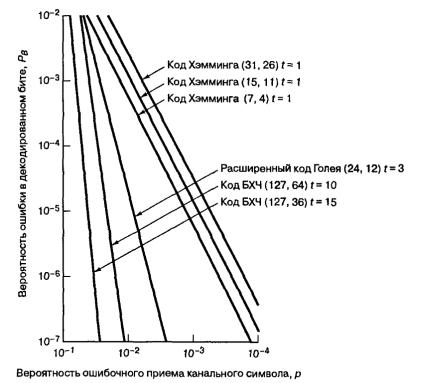
самостоятельно. Отметим лишь, что уменьшение вероятности ошибки p на вы-
ходе демодулятора вызывает резкое снижение вероятности ошибки (на 1 бит)
на выходе декодера. Для кода с большей исправляющей способностью t график этой зависимости имеет более крутой рабочий участок. Известно [5], что отно-
сительно широкий максимум эффективности кодирования, в зависимости от скорости кодирования при фиксированном п, для кодов БХЧ находится в диа-
пазоне скоростей кодирования 1/3 и 3/4.
Рис. 3.1. Зависимость вероятности битовой ошибки от вероятности ошибки в каналь-
ном символе для некоторых кодов (Хэмминга, БЧХ, Голея)
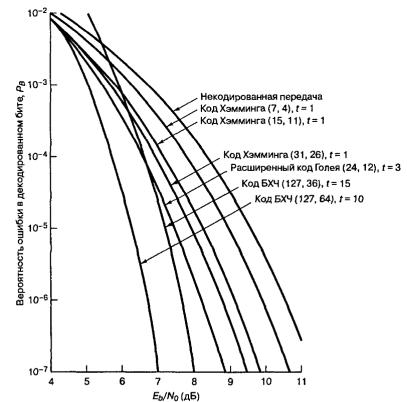
На рис. 3.2 показана зависимость Рв от Eдв/N0 для когерентно демодулиро-
ванного сигнала BPSK в гауссовском канале. Кривые, соответствующие кодам БЧХ, расположены левее остальных. Это означает, что использование кодов БЧХ позволяет получить больший энергетический выигрыш от кодирования,
чем коды Хэмминга или Голея, что объясняется лучшей исправляющей способ-
ностью кодов БЧХ. Полный анализ и сопоставление этих зависимостей студен-
ту предлагается проделать самостоятельно.
20
На рис. 3.3 показаны расчетные характеристики вероятности ошибки в де-
кодированном бите для когерентно демодулированного сигнала BPSK и кодов
БХЧ.
Рис. 3.2. Зависимость Рв от Eдв/N0 для когерентно демодулированного сигнала BPSK в
гауссовском канале для некоторых кодов (Хэмминга, БЧХ, Голея)
На рис. 3.3 построена серия графиков для кодов БЧХ со скоростью коди-
рования приблизительно равной ½ и жестким решением декодера. Для анализа выбран набор кодов БЧХ с увеличивающейся длиной n кодового слова. В таб-
лице 1 приведены основные параметры кодов, для которых построены зависи-
мости (рис. 3.3) вероятности ошибки от удельных затрат энергии на 1 бит ин-
формации.
Таблица 1.
Параметры кодов БЧХ, характеристики которых приведены на рис. 3.3
Длина кодового слова n |
31 |
63 |
127 |
511 |
1023 |
|
|
|
|
|
|
Длина информационного слова k |
15 |
35 |
63 |
249 |
502 |
|
|
|
|
|
|
Число проверочных бит r = n – k |
16 |
28 |
64 |
262 |
521 |
|
|
|
|
|
|
21
