Численные методы
.pdf
Оценка погрешности
Понятие о формулах интерполяционного типа
степени n с узлами интерполяции
и.
При этом справедлива оценка
25. Численное решение задачи Коши для ОДУ 1-го порядка. Постановка задачи. Дискретизация задачи Коши. Простейшая классификация методов (явные/неявные, одно/многошаговые).
Постановка задачи
Решением обыкновенного дифференциального уравнение первого порядка y’(t)=f(t,y(t)) называется дифференцируемая функция y(t), которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называют интегральной кривой.
Исходя из геометрического смысла производный y’ заметим, что уравнение задает в каждой точке (t,y) плоскости переменных t,y значения f(t,y) тангенса угла наклона α касательной к графику решения, проходящего через эту точку. Для того, чтобы выделить из семейства решений дифференциального уравнения одно конкретное решение, задают начальное условие
Теорема: пусть функция f(t,y) определена и непрерывна полосе . Предположим также, что она удовлетворяет условию Липшица
Для всех и произвольных Тогда для каждого начального значения определенное на отрезке .
,где L – некоторая постоянная (постоянная Липшица). существует единственное решение y(t) задачи Коши,
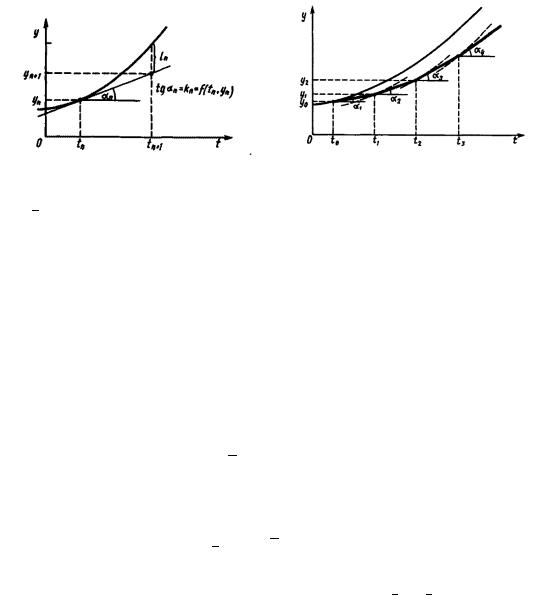
Задача вычисления сеточной функции удовлетворяющей уравнению и принимающей начальные значения называют дискретной задачей Коши.
При k=1 уравнение упрощается, и соответствующий метод называют одношаговым. При k>1 метод называют многошаговым.
Явные и неявные методы
В случае, когда функция Ф не зависит от метод называют явным. В противоположном случае, если функция зависит то неявный метод. Примером явного метода можно назвать метод Эйлера,
в котором вычисление |
производится по явной формуле. Для неявного, неявный метод |
Эйлера. |
|
26. Явный метод Эйлера решения задачи Коши. Геометрическая иллюстрация. Погрешность аппроксимации, сходимость. Недостатки метода.
Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, т. н. ломаной Эйлера
.
погрешность аппроксимации
Недостатки
1)При попытках увеличить точность за счет уменьшения шага, приводит к резкому росту погрешности
2)Если требуется высокая точность решения, то достигнуть с помощью метода Эйлера нельзя.
27. Метод ЭйлераКоши и усовершенствованный метод Эйлера решения задачи Коши. Получение расчетных формул, геометрическая иллюстрация, порядок аппроксимации.
Метод Эйлера Коши
Усовершенствованный метод Эйлера
Получение расчетных формул
Пусть y(t) – решение дифференциального уравнения y’(t)=f(t,y(t)), удовлетворяющее условию
. Далее, пусть
Угловой коэффициент секущейц, проходящей через точки |
и |
графика |
функции y(t). Ясно, что метод, состоящий в вычислении по формуле |
|
имеет |
нулевую локальную погрешность. Для того чтобы воспользоваться этой формулой, нужно лишь «научится вычислять значение ». Интегрируя обе части уравнения по t приходим к равенству
Применяя формулу трапеций для вычисления приводит к методу Эйлера-Коши. Метод имеет второй порядок точности.
Еще одну модификацию второго порядка точности можно получить с помощью формулы центральных прямоугольников
Если для приближенного вычисления |
|
применить метод Эйлера. В результате получим |
расчетные формулы усовершенствованного метода.
28. Неявный метод Эйлера решения задачи Коши. Погрешность аппроксимации. Абсолютная устойчивость на модельном уравнении. Понятие о жестких задачах
Неявный метод Эйлера
Достаточным условием устойчивости неявного метода Эйлера является выполнения условия
Оценка погрешности
Абсолютная погрешность на модельном уровне
Метод называется абсолютно устойчивым для данного z=hλ, если при этом z все корни полинома устойчивости
Лежат в комплексной плоскости внутри единичного круга и на границе этого круга нет кратных корней.
Понятие о жестких задачах
При решении задачи Коши явными методами Рунге-Кутты и Адамса сталкиваются с весьма неожиданными явлениями. Несмотря на медленное изменение искомых функций, расчет приходится вести, казалось бы, с неоправданно мелким шагом h. Все попытки увеличить шаг и тем самым уменьшит время, решения задачи приводят к катастрофически большому росту погрешности. Подчеркнем, что жесткость является свойством задачи Коши (а не методов).
29. Метод Рунге-Кутты. Общая формула m-этапного метода. Однопараметрическое семейство явных двухэтапных методов Рунге-Кутты 2-го порядка.
Метод Рунге-Кутты Общая формула m-этапного метода
Семейство явных двухэтапных методов
Теорема: Пусть правая часть дифференциального уравнения удовлетворяет условию |
. |
||||||
Тогда всякий m-этапный метод Рунге-Кутты устойчив на конечном отрезке. |
|
||||||
Следствие: Пусть выполнено условие |
. Тогда если явный m-этапный метод Рунге-Кутты |
||||||
имеет р-й порядок аппроксимации, то он сходится с р-м порядком точности |
|
||||||
Можно утверждать, что при любом |
метод |
|
|
|
|||
|
|
|
|
|
|
имеет второй порядок |
|
|
|
|
|
|
|
||
точности. При |
формула дает метод Эйлера Коши, а при |
|
– усовершенствованный метод |
||||
|
|||||||
Эйлера. |
|
|
|
|
|
|
|
30. Методы, основанные на использовании формулы Тейлора. Недостатки. Правило Рунге оценки погрешности решения задачи Коши.
Формула Тейлора
Использование формулы Тейлора приводит к следующему явному одношаговому методу:
Здесь .
Недостатки
Использование этой формулы приводит к необходимости вычисления большого числа частных производных, что чаще всего является весьма трудоемкой и нередко аналитически невыполнимой операцией.
Правило Рунге.
Правило Рунге — правило оценки погрешности численных методов.
Основная идея (для методов Рунге-Кутты решения ОДУ) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.
31. Краевая задача для ОДУ 2-го порядка. Постановка задачи в случае постоянного коэффициента теплопроводности. Дискретизация. Построение разностной схемы методом конечных разностей. ее разрешимость.
Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.
Решение краевой задачи ищется в виде линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями
– краевая задача для ОДУ-2го порядка.
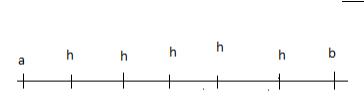
Дискретизация области вводим сетку
Теорема о разрешимости
Пусть коэффициент q и f являются m раз, а коэффициент k- m+1 раз непрерывно дифференцируемыми на отрезке [a,b] функциями. Тогда решение и краевой задачи является m+2 раза непрерывно дифференцируемой на отрезке [a,b] функцией.
Разностная схема методом конечных разностей.
32. Разностная схема для краевой задачи для ОДУ 2-го порядка. Аппроксимация. Устойчивость и сходимость PC (без доказательств)
Разностная схема для краевой задачи
Устойчивость
Назовем разностную схему устойчивой, если при любых |
, |
справедлива оценка |
Где постоянная K не зависит от h.
Аппроксимация
Пусть u(x) – решением дифференциального уравнения L[u]=f назовем сеточную функцию погрешностью аппроксимации разностного уравнения
Из определения |
следует, что справедливо неравенство |
означающее, |
|
что функция u удовлетворяет разностному уравнению с точностью до погрешности |
|||
аппроксимации. |
|
|
|
Сеточную функцию |
используют для предварительной оценки того, насколько точно |
||
аппроксимируется дифференциальное уравнение его разностным аналогом. Говорят что |
|||
разностное уравнение аппроксимирует дифференциальное уравнение L[u]=f |
, если |
||
|
при h |
, и аппроксимирует его с m-м порядком (при m>0) если справедлива |
|
оценка |
|
|
|
Справедлива оценка
Сходимость |
|
|
|
Разностная схема сходится при h |
если |
, и сходится с m-м |
|
порядком точности ( при m>0), если для погрешности справедлива оценка |
где С – |
||
некоторая постоянная не зависящая от h. |
|
|
|
Тогда для погрешности разностной схемы справедлива оценка |
|
|
|
Где
33. Краевая задача для ОДУ 2-го порядка. Дискретизация задачи в случае непостоянного коэффициента теплопроводности. Правило Рунге оценки погрешности решения.
– краевая задача для ОДУ-2го порядка
Правило Рунге оценки погрешности решения.
Пусть решения разностной схемы. Соответствующие тогда в соответствии с правилом Рунге при определенных условиях справедлива приближенная формула
Дискретизация – приближенная замена исходной задачи конечномерной задачей, т.е. задачей, входные данные и искомое решение которой могут быть однозначно заданы конечным набором чисел.
34. Начально-краевая задача для одномерного уравнения теплопроводности. Явная разностная схема: порядок аппроксимации, условие устойчивости.
Явная разностная схема
Устойчивость Теорема: для разностной схемы справедлива оценка
С постоянной |
. |
35.Начальная краевая задача для одномерного уравнения теплопроводности. Чисто неявная разностная схема: порядок аппроксимации устойчивость. Реализация разностной схемы.
Неявная разностная схема
36. Задача Дирихле для уравнения Пуассона. Разностная схема «крест». Реализация PC с помощью методов Якоби и Зейделя.
Задача Дирихле — задача отыскания в области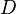 
евклидова пространства гармонической функции 
, которая на границе 
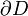области 
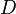совпадает с наперёд заданной непрерывной
функцией 
. Задачу отыскания регулярного в области решения эллиптического уравнения 2-го порядка, принимающего наперед заданные значения на границе области, также называют задачей Дирихле, или первой краевой задачей.
разностная схема «крест»
Методы решения разностной задачи Дирихле
Рш
Я
З
s = 0
37. Начально-краевая задача для волнового уравнения. Постановка задачи. Дискретизация (трехслойная разностная схема), аппроксимация, условие устойчивости. Проблема «запуска» разностной схемы.