28. Принципы построения алгоритмов автоматизированного проектирования оптимальных магнитных систем с применением численного анализа полей. Оптимизация с применением промежуточной аппроксимации функциональных ограничений.

Ответ.

Этот метод рассмотрен нами на примере следующей задачи.

Задача. Цилиндрический постоянный магнит с однородной намагниченностью по оси М=1000 кА/м должен притягиваться к стальному диску (Сталь 10) с силой F. Определить оптимальные размеры постоянного магнита (D,L) по критерию минимума объема постоянного магнита.

Методические указания

1. Определить начальное приближение размеров магнита . Для этого построить однофакторные зависимости:.

2. Определить коэффициенты приближенной зависимости силы от размеров, используя квадратичную аппроксимацию:

.

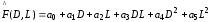Для расчетов построить таблицу для 9 точек (пар чисел 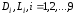при варьировании переменными в пределах.

№ вар.	D, мм	L, мм	F, расч., Н	, Н
1			F1
2			F2
3			F3
4			F4
5			F5
6			F6
7			F7
8			F8
9			F9

3. Составить и решить систему уравнений для неизвестных коэффициентов по полученной таблице, используя метод наименьших квадратов.

.

4. Построить график зависимости .

5. Построить график зависимости .

29. Определение параметров макромоделей электромеханических систем (тяговые характеристики, ЭДС, индуктивности) на основе численного анализа электромагнитных полей.

Ответ.

Из учебника.

3.4. Потокосцепления, индуктивности и эдс катушек

Точный расчет потокосцеплений катушек затрудняет существенное отличие магнитных потоков в витках из-за неоднородного поля вектора магнитной индукции и пространственной конфигурации намотки провода (рис. 3.21). Для расчета потокосцепления в катушке с общим числом витков выделяютгрупп витков, в которых числа витков равны. Группы витков выбирают из условия их приближенной замены одним контуром. Магнитный поток через ограниченную контуромповерхностьс меньшими вычислительными затратами рассчитывают через циркуляцию векторного магнитного потенциала по этому контуру

.

Потокосцепление всей катушки вычисляют сложением потокосцеплений выделенных групп витков:

,

где – число витков в-ой группе;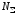- суммарное число витков в катушке.

ЭДС определяют дифференцированием по времени потокосцепления: . При анализе процессов в частотной области для синусоидальных полей в линейных средах используют комплексную форму записи индуцируемой в катушке ЭДС:. Если изменение потокосцепления вызвано изменением собственного тока в катушке, то возникающую ЭДС можно представить виде напряжений на эквивалентных сопротивлениях резистораи катушки индуктивности:

,

где определяется мнимой частью потокосцепления, а— действительной частью потокосцепления. В эквивалентной схеме электрической цепи вместо ЭДС включают резистор и катушка индуктивности, напряжение на которых равно и имеет обратный знак индуцированной в катушке ЭДС, вызванной изменением потокосцепления от собственного тока и всех вторичных процессов, инициированных этим током: индуцированные токи и перемагничивание сердечников катушек. При этом вторичные процессы линеаризуют (обычно приближенно). Мощность потерь равна выделяемой мощности на этом резисторе и последовательно включенном с ним резисторе, имеющем сопротивление провода на постоянном токе.

Пример 3.9. Необходимо определить зависимость индуктивности и активного сопротивления катушки со стальным сердечником от частоты.

На сплошном стальном кольце намотана катушка (рис. 3.22). Внешний и внутренний диаметры кольца соответственно 120 мм и 100 мм. Высота кольца 10 мм. Относительная магнитная проницаемость материала кольца , электрическая проводимостьМСм/м. Катушка имеет 72 витка и активное сопротивление провода на постоянном токе 32.8 мОм. Для расчетов электромагнитного поля использован метод, приведенный в п. 3.3.4. При амплитуде синусоидального тока в катушке 2.0 А и частоте 200 Гц, получены распределения действительной и мнимой компонент источников электромагнитного поля в поперечном сечении сердечника: намагниченности, индуцированных токов и зарядов, показанные на рис. 3.23. Из-за возникновения индуцированных токов действительная компонента намагниченности в центральной части сердечника уменьшается и появляется мнимая компонента намагниченности, имеющая обратное направление. Индуцированные токи образуют замкнутые структуры в сечении сердечника, причем плотность токов уменьшается к центральной части сердечника. Электрические заряды появляются только на поверхности кольцевого сердечника. Знаки и значения плотности зарядов согласуется с картиной распределения токов: на участках периметра сечения сердечника, где векторы плотностей тока направлены внутрь сечения, заряды положительные, в противном случае – отрицательные. Зависимости активного сопротивления и индуктивности катушки от частоты показаны в виде графиков на рис. 3.24. Возникновение индуцированных токов приводит к уменьшению индуктивности и возрастанию активного сопротивления с ростом частоты.