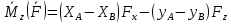- •18) Условие жёсткой связи; неизменяемые мех-е сис-мы; Конфигурация мат-го тела; Теорема Грасгофа о проекциях скоростей.
- •19)Допустимые конфигурации мех. Сис-м;Коллинеарные точки неизменяемой мех. Сис-мы; Теорема о скоростях коллин. Точек.
- •20)Основное св-во допустимой конфигурации абсолютно тв. Тела; Задание конфигурации тв. Тела методом 3-х точек.
- •21)Связанная сис-ма отсчёта. Задание конфигурации атт методом связанных осей. Нахождение текущего положения телесной точки по её координатам в связанных осях.
- •22)Оператор ориентации абсолютно твёрдого тела. Ортогональность оператора ориентации. Основная формула геометрии движения.
- •23)Поступательное движение тв. Тела. Теорема о критерии поступательного движения. Траектории, скорости и ускорения телесных точек при поступательном движении.
- •24)Компоненты и матрица линейного оператора; формулы для компонент линейного оператора. Матрица направляющих косинусов тв. Тела.
- •25)Транспонирование линейных операторов. Св-ва матрицы направляющих косинусов.
- •1)Момент силы относительно точки
- •2)Вычисление проекции момента силы. Антисимметричные матрицы. Момент силы относительно оси
- •4)Аксиомы статики: общие аксиомы о силах. Следствие о переносе силы вдоль линии действия
- •10)Условия равновесия твёрдого тела при наличии трения(точечный и поверхностный контакт)
- •12) Способы задания движения точки
- •13) Скорость точки в в-ом и координатном способах задания движения
- •14)Скорость при естественном способе задания движения точки
- •17)Лемма об уравнениях сближения двух точек по экспоненте
- •3)Сис-мы сил и их эквивалентность. Главный вектор и главный момент сис-мы сил. Теорема об изм-ии гл. Момента при смене полюса.
- •5) Аксиомы статики: аксиома о связях. Реакции связей.
- •6) Теорема о приведении произвольной системы сил к двум силам.
- •7) Пара сил, её плечо и момент. Теорема о приведении произвольной сис-мы сил к силе и паре.
- •8) Теорема об условиях равновесия атт. Ур-я равновесия для пространственной сис-мы сил
- •9)Ур-е равновесия для плоской и сходящейся сис-мы сил, для сис-мы параллельных сил. Статистически определяемые задачи.
- •11)Законы трения скольжения(при покое). Закон Амантона-Кулона. Задача о трибометре.
24)Компоненты и матрица линейного оператора; формулы для компонент линейного оператора. Матрица направляющих косинусов тв. Тела.
Пусть
 {
{ }
} – базисы в X и Y
– базисы в X и Y
Коэффициенты
 в
расположении
в
расположении называются компонентами оператора
называются компонентами оператора ,
а составленная из этих компонент матрица
с – матрица данного оператора.
,
а составленная из этих компонент матрица
с – матрица данного оператора.
Если
пр-во Х и Y евклидовы, а базисы
 -
ортонормированные, то
-
ортонормированные, то
(*)
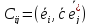
Это
следует из ф-лы
 дляi-той
компоненты вектора
дляi-той
компоненты вектора
 в ортонормированном базисе.
в ортонормированном базисе.
Пусть
А*х*у*Z* - сис-ма координат в СО, связанной
с АТТ
 а охуz – неподвижные оси координат
а охуz – неподвижные оси координат
Для
компонент
 оператора
ориентации
оператора
ориентации имеем:
имеем:
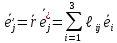 ; здесь{
; здесь{ }-
связанный базис, {
}-
связанный базис, { }
– неподвижный базис, а
}
– неподвижный базис, а - единичные векторы подвижных осей
Ах'y'z' (т.е. осей A*x*y*z*, отнесённых к у.н.
СО)
- единичные векторы подвижных осей
Ах'y'z' (т.е. осей A*x*y*z*, отнесённых к у.н.
СО)
В
силу (*):

Компоненты
 оператора ориентации, иначе именуютсяНаправляющими
косинусами
осей x'y'z' по отношению к осям xyz, а его
матрицу
оператора ориентации, иначе именуютсяНаправляющими
косинусами
осей x'y'z' по отношению к осям xyz, а его
матрицу
Г называют
Матрицей направляющих косинусов тела
называют
Матрицей направляющих косинусов тела
 .
.
25)Транспонирование линейных операторов. Св-ва матрицы направляющих косинусов.
Пусть
 ,
а пр-ваX,Y
– евклидовы. Оператор
,
а пр-ваX,Y
– евклидовы. Оператор
 называется транспонированным оператором
для оператора
называется транспонированным оператором
для оператора ,
если
,
если
Имеем:

Вывод:
матрица
 транспонированного оператора
транспонированного оператора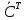 получается из матр. С оператора
получается из матр. С оператора транспонированым.
транспонированым.
Св-ва матрицы напр-х косинусов:
1)Матр. Напр. Кос. Г – собственная ортогональная:
-

- det Г = 1 (определитель)
2) у матр. Г:
- скалярный квадрат каждого столбца(строки) = 1
- скалярные произведения разных столбцов(строк) = 0.
1)Момент силы относительно точки
Момент
силы относительно полюса В-вектор
приложенный в т.В и = векторному произв
радиус вектора т. приложения на вектор
силы:
 Основны с-ва вытекают из с-в в-во умножения
Основны с-ва вытекают из с-в в-во умножения
Свойства:
1)Переход
от силы к её моменту-линейная операция
 ,если
силыF
и G
прилож в одной т.
,если
силыF
и G
прилож в одной т.

2)Модуль
момента силы определяется ф-лой

3)Направление
момента силы определяется условиями
 ,
и в-ры
,
и в-ры
Образуют правую тройку в-ов
4)
Линия действия силы – прямая, проходящая
в направлении силы через точку её
приложения
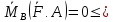 полюс
В лежит на линии действия силы. Момент
силы хорактерезует вращательный эффект
силы
полюс
В лежит на линии действия силы. Момент
силы хорактерезует вращательный эффект
силы
Плечо
силы - кратчайшее расстояние от полюса
до линии действия силы
2)Вычисление проекции момента силы. Антисимметричные матрицы. Момент силы относительно оси
 ,
где
,
где
 -компоненты
в-ра
-компоненты
в-ра в осяхOxyz;
в осяхOxyz;
 ,
где x,y,z-
координаты т.А в осях Oxyz
,
где x,y,z-
координаты т.А в осях Oxyz
Момент
силы
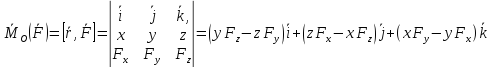
Компоненты
в-ра
 в
осяхOxyz
в
осяхOxyz
(*)
Введём
столбцы компонент в-ов

 р-во
сводится к одному матричному р-ву
р-во
сводится к одному матричному р-ву
 ,
если
,
если
 ,
матрица
,
матрица антисимметрична
антисимметрична
Последнюю
ф-лу (*) можно представить в виде (**) - Ф-лаПуансо,
тк в неё не входит z,
след проэкция момента ситы на ось не
изменится, при сдвиге полюса вдоль этой
оси.
- Ф-лаПуансо,
тк в неё не входит z,
след проэкция момента ситы на ось не
изменится, при сдвиге полюса вдоль этой
оси.
Момент
силы относительно оси-
скалярная величина = проекции на эту
ось момента силы относительно точки,
лежащей на данной оси. Можно вычислить
проэцируя р-ро на ось BZ
 ,
вместо последней ф-лы(*)
,
вместо последней ф-лы(*)