18) Условие жёсткой связи; неизменяемые мех-е сис-мы; Конфигурация мат-го тела; Теорема Грасгофа о проекциях скоростей.

- Жесткая связь(наложенная на точки А и В ϵ S’)

В этом случае в любом движении сис-мы выполнено условие: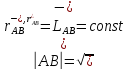

Смысл его: расстояние между текущими положениями точек остаётся постоянным.

Иная форма записи условия жёской связи: (**))=

В координатах: .

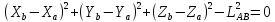-Механическая система – неизменяемая, если расстояния между положениями 2-х её точек остаются постоянными, каким бы воздействиям она не подвергалась

Частые случаи: 1. Неизменяемая СМТ. 2. Абс. Твёрдое тело(АТТ)

Если B – мат. тело, то в момент времени t положение его точек непрерывно заполняют(по аксиоме сплошности) в у.н. СО ε некоторую область ε

Отображение Н: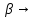ε сопоставляющее каждой точке тела её текущее положение ву.н. СО, называется конфигурацией тела (в текущий момент времени

Она задана, если указано правило, по кот-му можно найти текущее положение любой точки тела.

Если А,В – текущие положения точек А* и В* тела , то это означает: А=Н(А*), В=Н(В*)

Условие вида (**) должно выполняться для любых 2-х точек неизменяемое сис-мы (будучи либо усл. Одной из связей, либо следствием из усл. Других связей).

-Теорема Грасгофа о проекциях скоростей.

Если на точки А* и В* наложена жесткая связь, то проекции их скоростей на прямую, соединяющую текущие положенияэтих точек равны:

Д-во: достаточно доказать, что:

Диф-я по t условие жёской связи 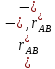)=const, получаем (

Итак, , т.е.

Пусть теперь - ед. вектор оси АВ. Имеем:=

Замечание: т-ма Грасгофа верна для точек неизменяемой сис-мы(в частности АТТ).

19)Допустимые конфигурации мех. Сис-м;Коллинеарные точки неизменяемой мех. Сис-мы; Теорема о скоростях коллин. Точек.

Конфгурация мех. сис-мы допустимая, если:

-положения всех точек сис-мы удовлетворяют намеченным на неё геом. связям(осн. требование)

-данную конфигурацию можно получить из отсчётной непрерывным движением, не нарушающим связей(доп. требование)

Покажем, что если для какой-либо конфигурации неизменяемой сис-мы текущие положения её точек А*, В*, С* коллинеарны(лежат на одной прямой), то и для любой допустимой конфигурации они будут коллинеарны.

В самом деле, если бы не лежала на прямойто было бы:

||+||>||=||=||+||

В случае неизменяемой сис-мы считаем, что точки: Коллинеарны, если коллин. их положения

Теорема о скоростях коллин. точек.

Концы скоростей точек неизм. сис-мы, лежащих на одной прямой, также лежат на одной прямой и делят её на части пропорциональные расстояниям между точками

Док-во: зафиксируем ед. изм-я времени, выбрав масштаб для геометр. Изображения скоростей.

Дифференцируем (*) по t, получим (**)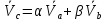

Складывая(*) и (**) получаем:

Значит лежит на прямой

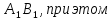
|||==|AC|:|CB| ч.т.д.

20)Основное св-во допустимой конфигурации абсолютно тв. Тела; Задание конфигурации тв. Тела методом 3-х точек.

-метод 3-х точек:

В данном методе в теле выбирают неколлинеарные точки А*,В*,С*.

Конфигурацию АТТ задают, указав текущие положения этих точек: А=Н(А*), В=Н(В*), С=Н(С*)

Здесь Н: C – конфигурация АТТ

Вектор является таким вектором нормали в плоскости АВС, что с его конца обходвиден происходящим против часовой стрелки.

-Основное св-во доп. конфигурации АТТ – она сохраняет расстояние между его точками. Поэтому должны выполняться требования:

|AB|=|A*B*|,|CA|=|C*A*|,|BC|=|B*C*|