Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции

Так же, как и в действительном анализе, для функций комплексного переменного вводится понятие производной. Однако здесь это понятие более глубокое, чем в действительном анализе. Например, всякая линейная действительная функция дифференцируема в любой точке. Для комплексных функций это не так. Например, функция нигде не дифференцируема. Перейдём к изучению этого понятия.

1. Производная функции комплексного переменного. Условия Коши-Римана. Аналитичность функции

Пусть функция 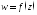определена в точкеи некоторой ее окрестностиСместимся из точкив точку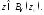Тогда аргумент функцииполучит приращение, а сама функция-- приращение

Определение 1.Если существует конечный предел

то его называют производной функции в точкеи обозначают

С понятием производной тесно связано понятие дифференцируемости функции в точке

функцияназывается дифференцируемой в точкеесли её приращение в этой точке представляется в виде

где постоянная, не зависящая отПри этом величинаназываетсядифференциалом функции в точкеи обозначаетсяРазделив обе части равенства (2) набудем иметьПоследнее равенство означает, что существует предел (1), т.е. что существует производнаяи что она равна Q. Таким образом,дифференцируемость функции в точкеэквивалентна существованию производной. При этоми значит,

Как уже отмечалось выше, не любая (даже очень простая) функция дифференцируема в точке Для этого её мнимая и действительные части должны быть определенным образом подчинены друг другу в следующем смысле.

Теорема Коши-Римана.Для того чтобы функциябыла дифференцируема в точкенеобходимо и достаточно, чтобы в точкееё действительная и мнимая части были дифференцируемы (как функции действительных переменных) и чтобы в этой точке имели место равенства

(равенства (3) называются условиями Коши-Римана).

Доказательство.Пусть функциядифференцируема в точке {\textit{}} Тогда имеет место асимптотическое разложение (2). Запишем его более подробно:

где ⁴. Отделяя здесь мнимые и действительные части, получим

Эти равенства означают, во-первых, что функции дифференцируемы как функции действительных переменныхив точкеи, во-вторых, что имеют место равенства

в точке Таким образом, если функциядифференцируема в точкето имеют место условия Коши-Римана (3). Рассуждая обратным ходом, покажем, что при выполнении условий (3) функциябудет дифференцируемой в точке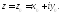Теорема доказана.

Замечание 1.Из доказательства теоремы следует, что если} дифференцируема в точкето ее производную в этой точке можно вычислять по формулеили по формуле.

Пример 1.Проверить, будет ли функциядифференцируемой. Если да, то найти её производную.

Решение.Выделим сначала вмнимую и действительные части:

Теперь проверим условия Коши-Римана. Имеем

значит, условия (3) Коши-Римана выполняются для всех Следовательно, функциядифференцируема в любой точкеЕё производную находим по формуле.

Таким образом, как и ожидалось, мы получили, что Забегая вперёд, отметим, что производные всех элементарных однозначных комплексных функций находятся по тем же правилам, что и производные действительных функций. Например,

То же замечание справедливо и для отдельных ветвей многозначных функций. Например,

Введём теперь следующее важное понятие.

Определение 2.Функцияназываетсяаналитической в точкеесли она дифференцируема как в точкетак и в некоторой её окрестности.

Аналитичность функции в точкеравносильна тому, чтоудовлетворяет условиям Коши-Римана (3) в некоторой окрестности точки(включая и саму точку

Определение 3. Функцияназывается аналитической (регулярной, голоморфной) в области}если она аналитична в любой точке этой области.

Заметим, что действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа: Это непосредственно вытекает из условий Коши-Римана. Функции, удовлетворяющие уравнению Лапласа, называютсягармоническими.

Пример 2.Является ли функцияаналитической хотя бы в одной точке?

Решение.Так как, то,. Условия Коши--Римана имеют вид:,и выполняются только в точке. Следовательно, функциядифференцируема только в точкеи нигде не аналитична. По определению запишем:. Таким образом, производнаясуществует и равна нулю.

Так как мнимая и действительная части аналитической функции связаны условиями Коши-Римана (3), тоопределяется (с точностью до постоянного слагаемого) либо своей действительной, либо мнимой частью. Покажем это на примере.

Пример 3.Найти аналитическую функцию, если известна ее мнимая частьдополнительном условии.

Решение.Так как, то из условий Коши-Римана (3) находим производные действительной части:

Решив первое из этих уравнений, находим где-- произвольная функция переменной. Для определениядифференцируемпо и подставляем в (2):, откудаи. Следовательно,и окончательно получим:

т.е. действительная часть восстанавливается с точностью до постоянного слагаемого. Условие позволяет найти эту постоянную однозначно:. Таким образом,.

Имеют место следующие утверждения.

1. Степенная функция с натуральным показателем аналитична во всей комплексной плоскостипричем

2. Каждая ветвь

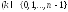- фиксировано) функциианалитична в областипричем

3. Комплексная экспонента аналитична во всей плоскости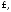причем

4. Комплексные тригонометрические функции ианалитичны во всей плоскостипричемТо же утверждение имеет место и для гиперболических функций, причем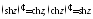

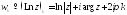
5. Каждая ветвь логарифми-

ческой функции аналитична в области причем

Все эти утверждения проверяются с помощью соотношений Коши-Римана.