КГТА

Типовой расчет №1

18 Вариант

Студент гр У-103

Проверил: Юлина

Задача 1. Бросаются две игральные кости. Определить вероятность того, что:

а) сумма числа очков не превосходит N;

б) произведение числа очков не превосходит N;

в) произведение числа очков делится на N.

N=12

Решение:

а)

-количество возможных исходов.

-количество благоприятных исходов.

б)

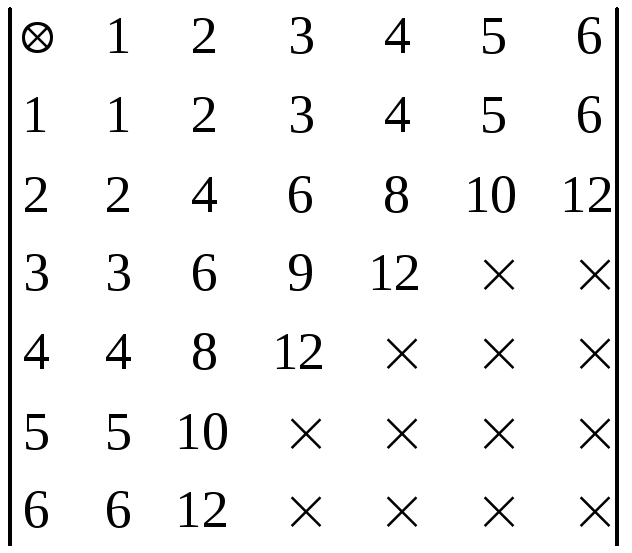
-количество возможных исходов

-количество благополучных исходов

в)

Ответ: 1; 0,64; 0,19.

Задача 3. Среди п лотерейных билетов k выигрышных. Наудачу взяли т билетов. Определить вероятность того, что среди них выигрышных.

, , ,

Решение:

Число возможных исходов:

Число благоприятных исходов:

5 выигрышных из 7 можно взять способами, а ещё 2 невыигрышных из 3 можно выбрать способами.

Ответ:

Задача 4. В лифт k - этажного дома сели n пассажиров (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что:

а) все вышли на разных этажах;

б) по крайней мере, двое сошли на одном этаже.

а) Количество возможных исходов:

Количество благоприятных исходов:

б) В задаче речь идёт про событие противоположное первому, значит

Ответ: , .

Задача 5. В отрезке единичной длины на удачу появляется точка. Определить вероятность того, что расстояние от точки до обоих концов отрезка превосходит величину . ()

Решение:

-длина отрезка, где появится точка.

-длина отрезка «благоприятного исхода»

Ответ:

Задача 7. В круге радиуса R наудачу появляется точка. Определить вероятность того, что она попадает в одну из двух непересекающихся фигур, площади которых равны и .

Решение:

Мера вероятности - площадь.

Все варианты попадания точки - в круг.

Благоприятные - в фигурах и

Ответ:

Задача 8. В двух партиях и % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:

а) хотя бы одно бракованное;

б) два бракованных;

в) одно доброкачественное и одно бракованное?

События:

А-из первой партии достали бракованное.

В-из второй партии достали бракованное.

а) С-хотя бы одно бракованное.

б) D-оба бракованных:

в) Е-одно бракованное и одно качественное.

Ответ:

Задача 9. Вероятность того, что цель поражена при одном выстреле первым стрелком , вторым - . Первый сделал , второй - выстрелов. Определить вероятность того, что цель не поражена.

Решение:

События:

Цель не поражена

А - первый стрелок промахнулся 3 раза

В - второй стрелок промахнулся 2 раза

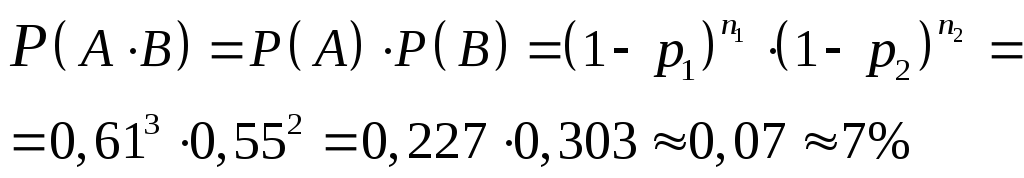
Ответ:

Задача 12. Из 1000 ламп принадлежат й партии, В первой партии 6%, во второй 5%, в третьей 4% бракованных ламп. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа - бракованная.

Решение:

Количество брака в первой партии:

Количество брака во второй партии:

Количество брака в третьей партии:

Ответ:

Задача 15. В магазин поступают однотипные изделия с трёх заводов, причём й завод поставляет % изделий . Среди изделий го завода % первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено третьим заводом.

Решение:

Ответ: 59%

Задача 17. Вероятность выигрыша в лотерею на один билет равна . Куплено билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.

Решение:

Найдём наивероятнейшее число выигравших билетов из неравенства:

Значит, есть два наивероятнейших числа 7 и 8.

Применима формула Бернулли:

Ответ:

Задача 19. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна Поступило вызовов. Определить вероятность «сбоев».

Так как и , то применима формула Пуассона.

Ответ: 13,2%

Задача 20. Вероятность наступления некоторого события в каждом из независимых испытаний равна Определить вероятность того, что число наступлений события удовлетворяют следующему неравенству: .

Решение:

Ответ: 0,994.

Задача 21. Дана плотность распределения случайной величины . Найти параметр , математическое ожидание , дисперсию , функцию распределения случайной величины , вероятность выполнения неравенства

Решение:

а) найдём параметр

б) найдём математическое ожидание :

в) найдём дисперсию :

г) Найдём функцию распределения случайной величины :

При

При

При

д)Найдём вероятность выполнения неравенства

Задача 27. Случайная величина имеет плотность распределения вероятностей . Найти плотность распределения вероятностей случайной величины

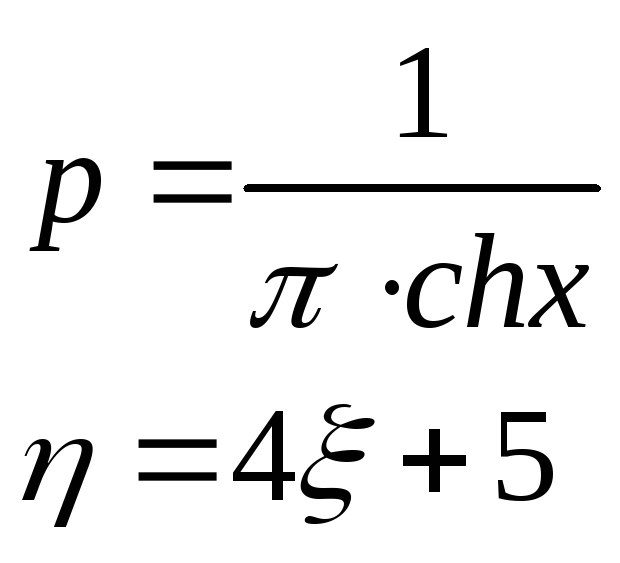
Так как функция монотонная, то:

Найдём производную:

Найдём интервал для

Проверка в системе MathCAD:

Задача 33. На отрезке случайным образом выбрано чисел, точнее, рассматриваются независимых случайных величин равномерно распределённых на отрезке . Найти вероятность того, что их сумма заключена между и т.е.

,

Решение:

Так как распределение равномерное, то

Ответ: 0,43 или 43%

Задача 34. Известно, что случайная величина имеет распределение Пуассона , неизвестным является параметр а. Используя указанный ниже метод получения точечных оценок, найти по реализации выборки значения оценки неизвестного параметра а (метод максимального правдоподобия)

Находим производную по а :

Находим вторую производную по а:

При максимум исходной функции. Значит

Ответ:

Задача 36. Случайная величина имеет нормальное распределение с неизвестным математическим ожиданием а и неизвестной дисперсией . По выборке объёма вычислено выборочное среднее . Определить доверительный интервал для неизвестного параметра распределения , отвечающий заданной доверительной вероятности .

Решение:

Ответ:

Задача 37. Случайная величина имеет нормальное распределение с неизвестным математическим ожиданием . По выборке объёма вычислены оценки:

и

неизвестных параметров. Найти доверительный интервал для математического ожидания а, отвечающей доверительной вероятности .

Решение:

Задача 41. Для контроля взяты 200 узлов, собранных на ученическом конвейере. Число узлов , при сборке которых пропущено операций, сведено в таблицу.

	0	1	2	3	4	5	6	>7
	41	62	45	22	16	8	4	0

Согласуются ли полученные результаты с распределением Пуассона (, где случайное число пропущенных операций) по критерию при уровне значимости ? Решить задачу для заданного значения параметра а, и для случая когда параметр а оценивается по выборке.

Решение: