О т в е т ы

1. .2. .3. а) ; б).

4. . 5. .6. .7. .8. .

9. .10. .11. .12. .

13. .14. .

8. Системы случайных величин

Функцией распределения системы двух случайных величин называется функция.

Для системы непрерывных случайных величин существует плотность распределения вероятностей, определяемая следующим образом:

.

Плотность распределения вероятностей неотрицательна:

.

Плотности распределения вероятностей случайных величин, входящих в систему:

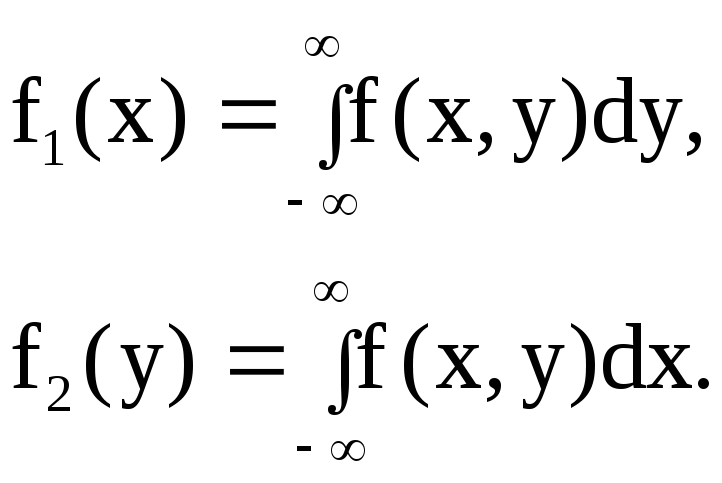
Случайные величины называютсянезависимыми, если

.

Система двух дискретных случайных величин может быть задана таблицей, в которой приведены пары значений случайных величин и соответствующие им вероятности.

Величины				…
				…
				…
				…
…	…	…	…	…	…
				…

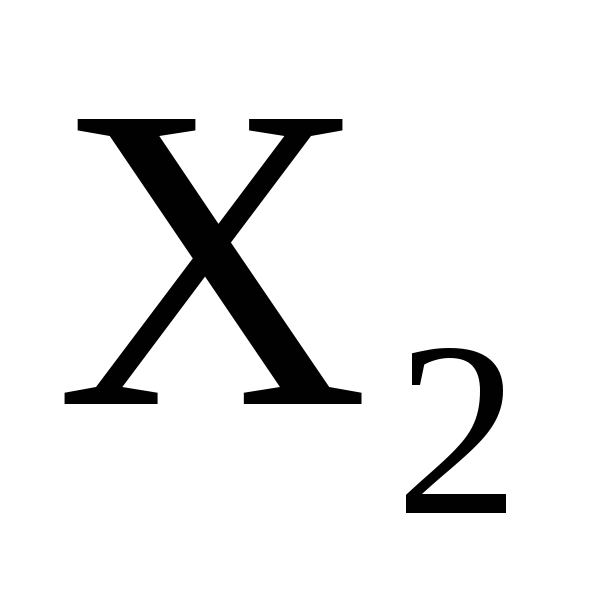
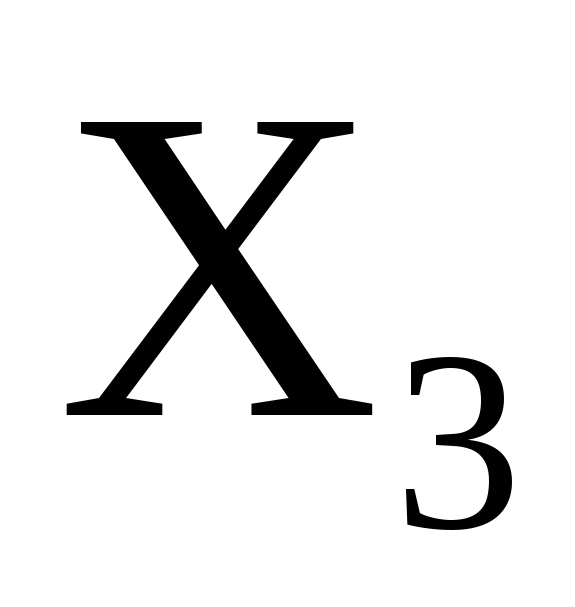
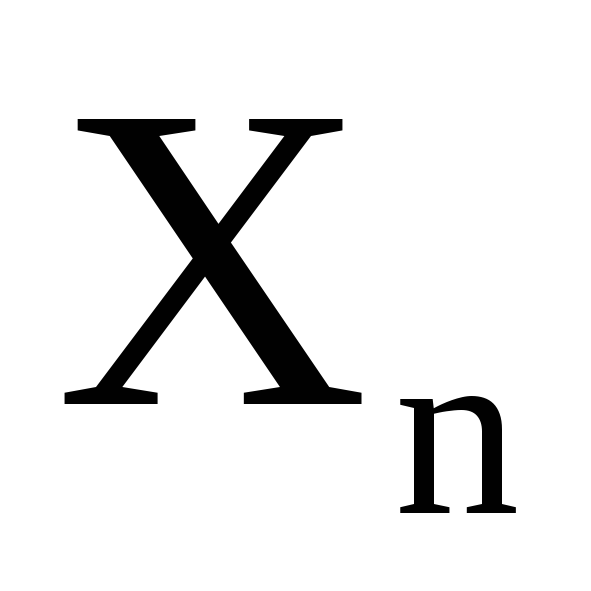
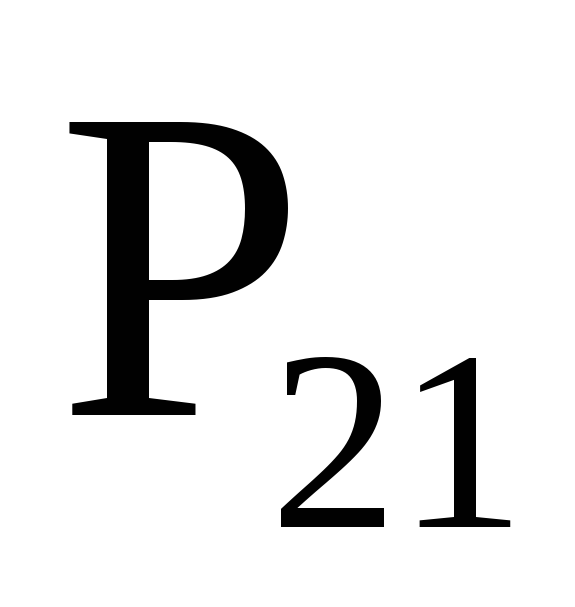
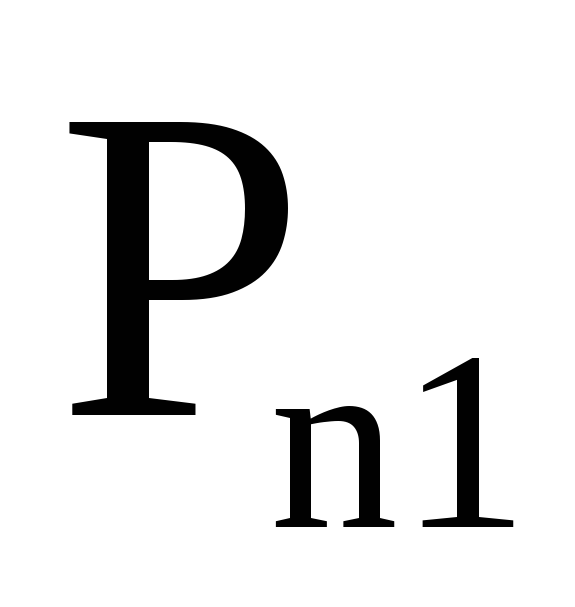
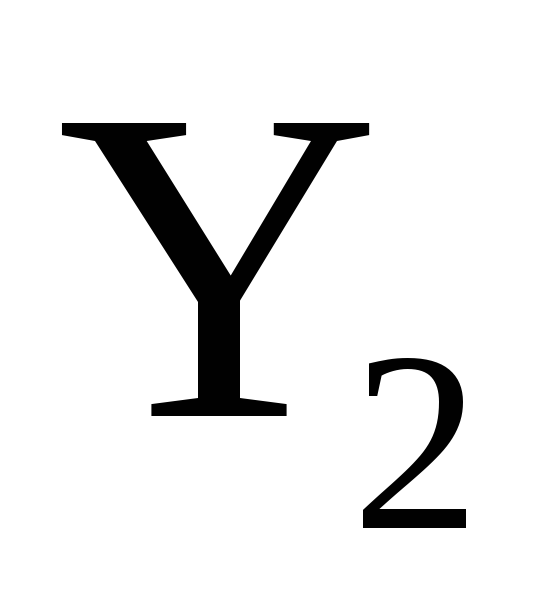
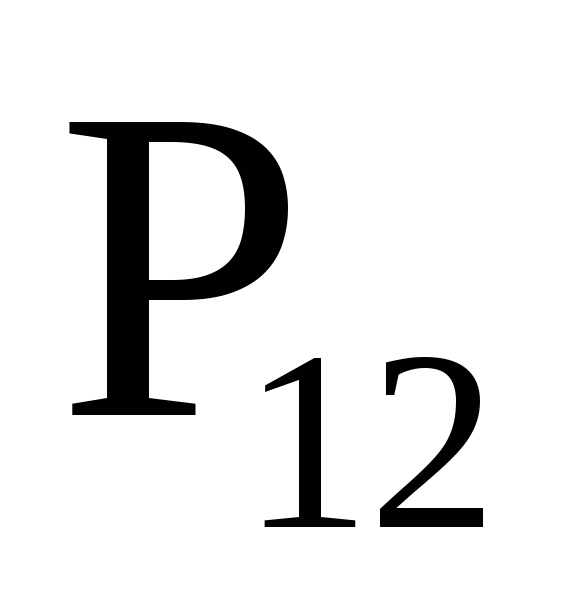
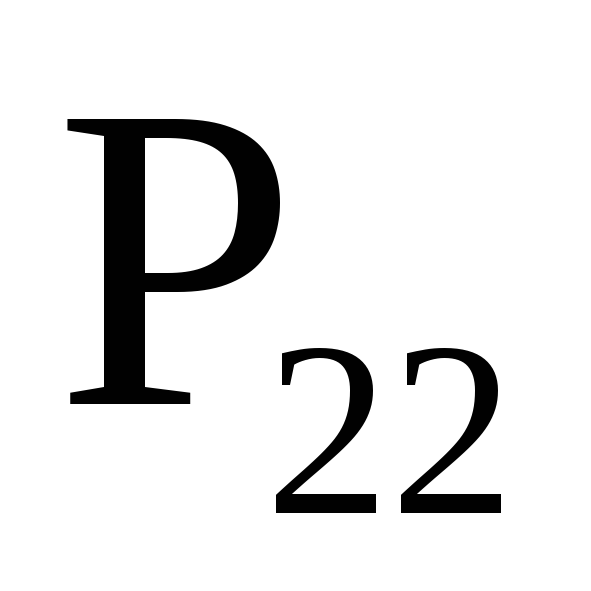
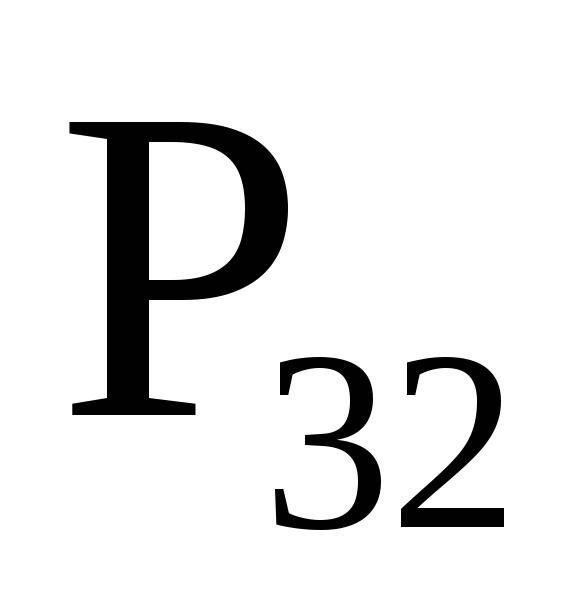
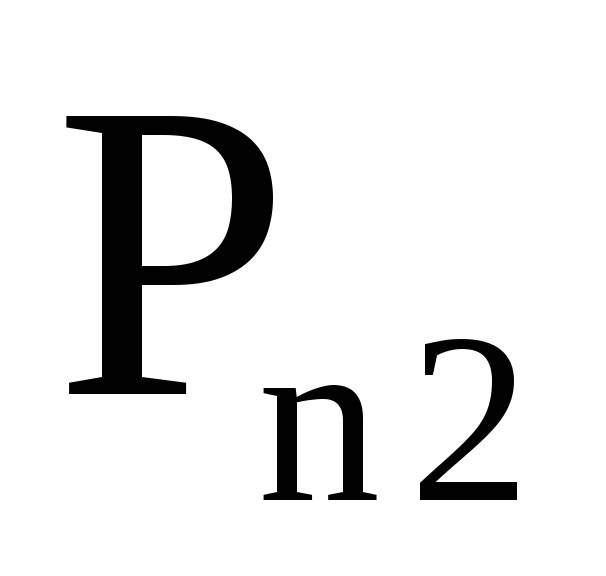
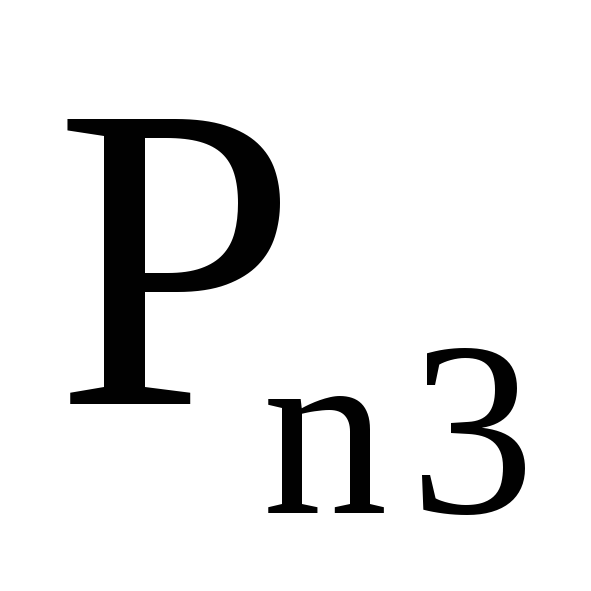
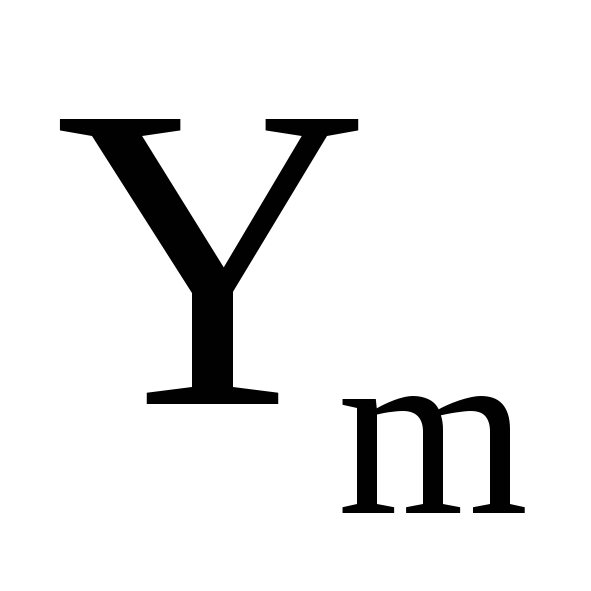
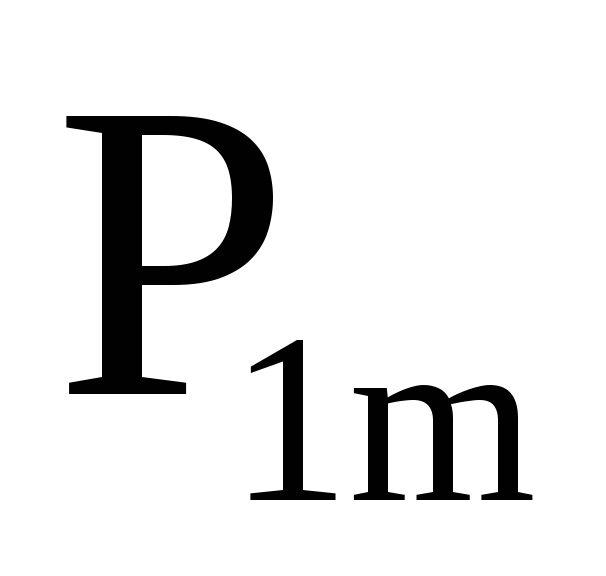
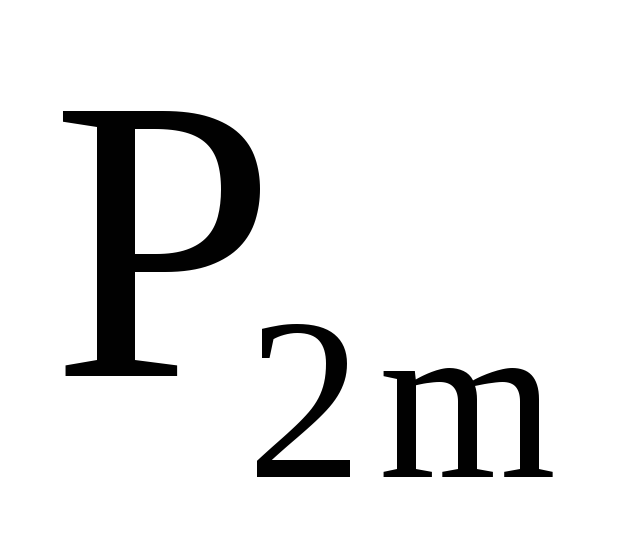
Здесь - вероятность события, заключающегося в одновременном выполнении равенств. При этом. Вышеприведенная таблица может содержать счетное множество строк и столбцов.

По таблице распределения вероятностей системы случайных величин можно найти закон распределения случайных величин, входящих в систему:

, .

Дискретные случайные величины называются независимыми, если

.

Начальный и центральный– моменты системы двух случайных величин определяются следующим образом:

и могут быть вычислены по формулам

,

(для дискретных случайных величин)

и ,

(для непрерывных случайных величин).

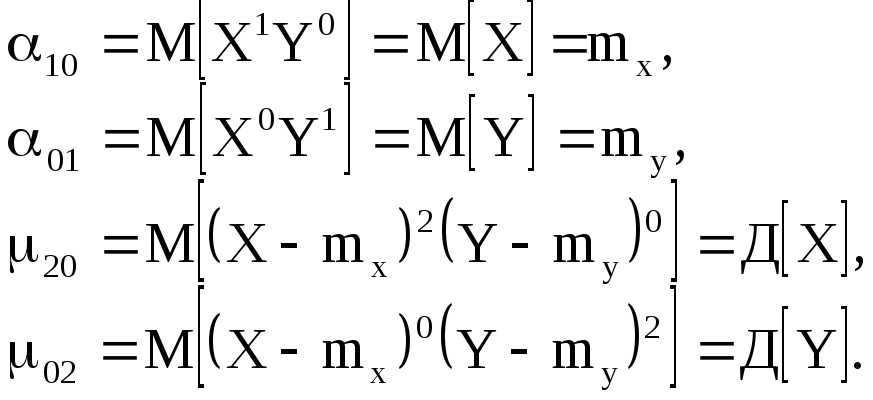
Центральный момент называетсякорреляционным моментом. Корреляционный момент характеризует степень линейной зависимости случайных величин. Безразмерной характеристикой связи между случайными величинами служит коэффициент корреляции

.

Если случайные величины, входящие в систему, независимы, то ; в общем случае из-за некоррелированностине следует независимость случайных величин.

Решение типовых задач

1. В двух ящиках содержатся шары, по 6 шаров в каждом. В ящике 1 шар – с № 1, 2 шара с № 2, 3 шара с № 3; во втором ящике – 2 шара с № 1, 3 шара с № 2 и 1 шар с № 3. Рассматриваются случайные величины: - номер шара, вытянутого из первого ящика;- номер шара, вытянутого из второго ящика. Из каждого ящика вынули по шару. Составить таблицу распределения системы случайных величин. Найти математические ожидания, дисперсиии, коэффициент корреляции.

Решение

	1	2	3
1
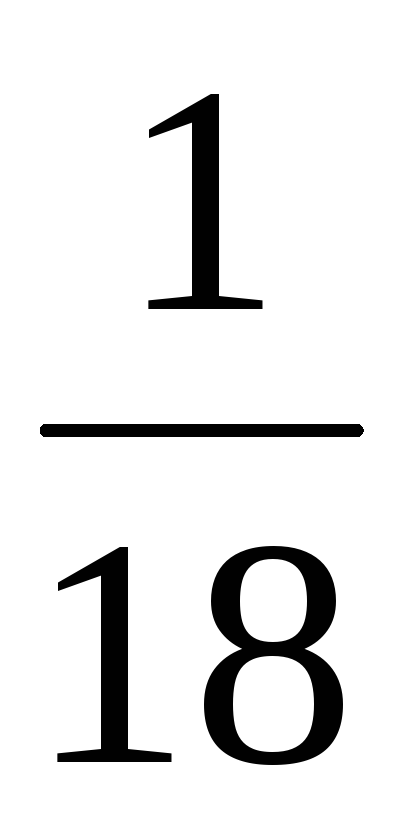
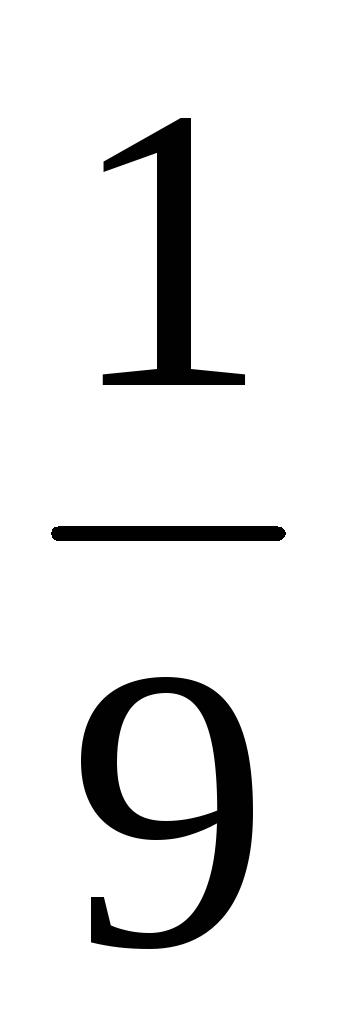
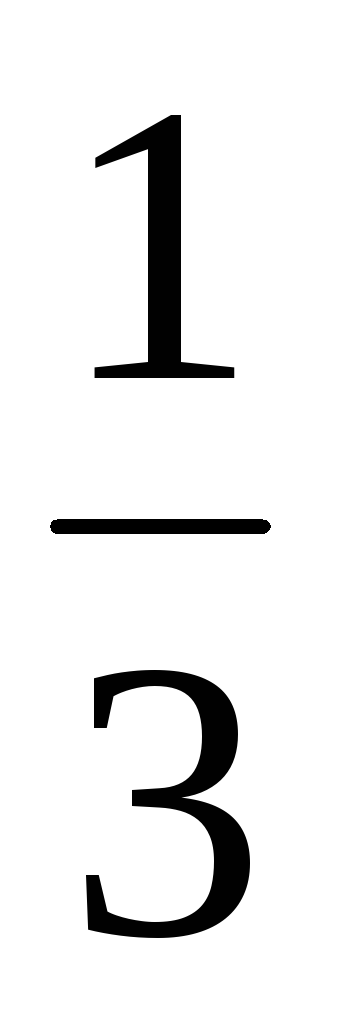
2
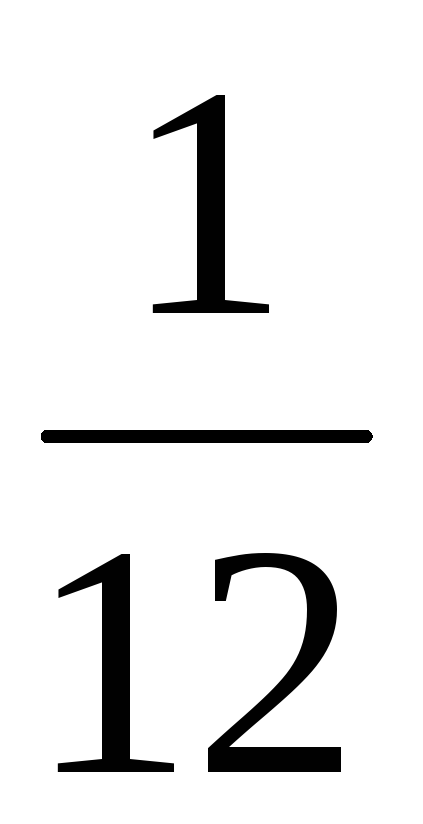
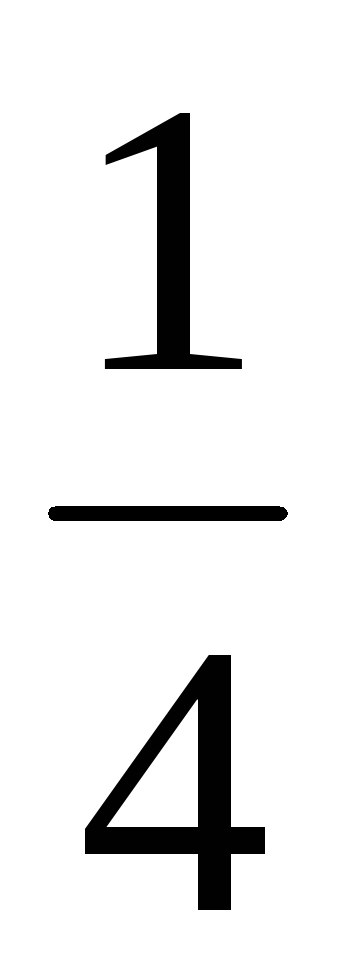
3

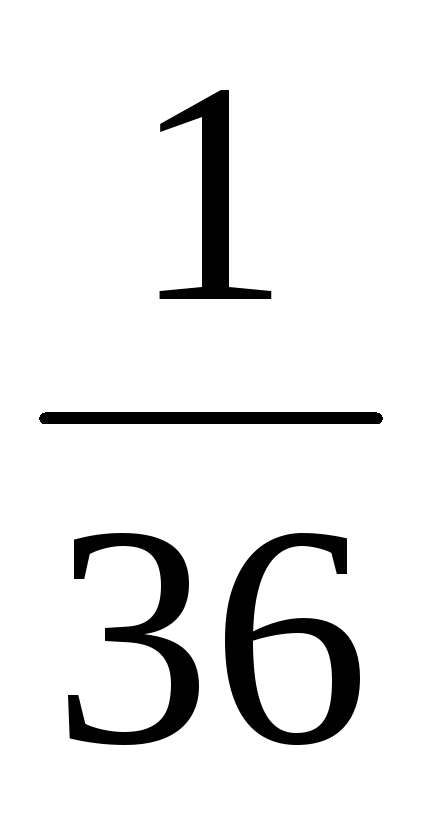
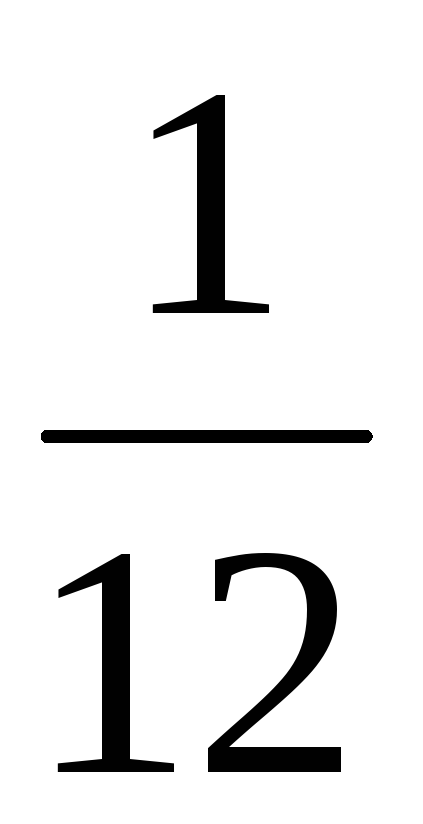
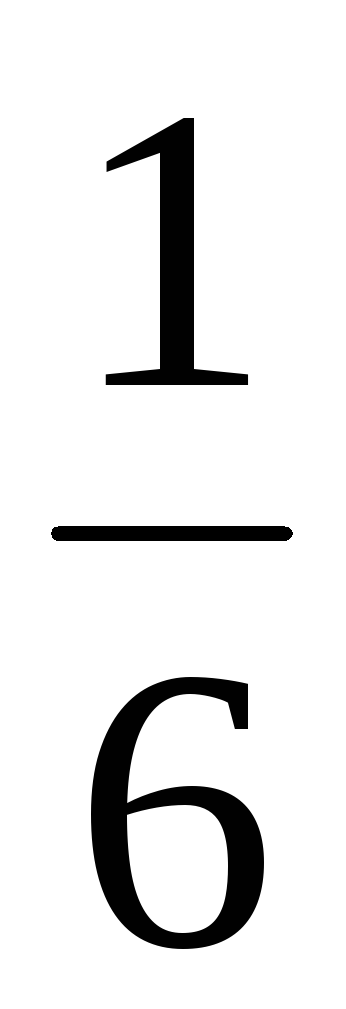
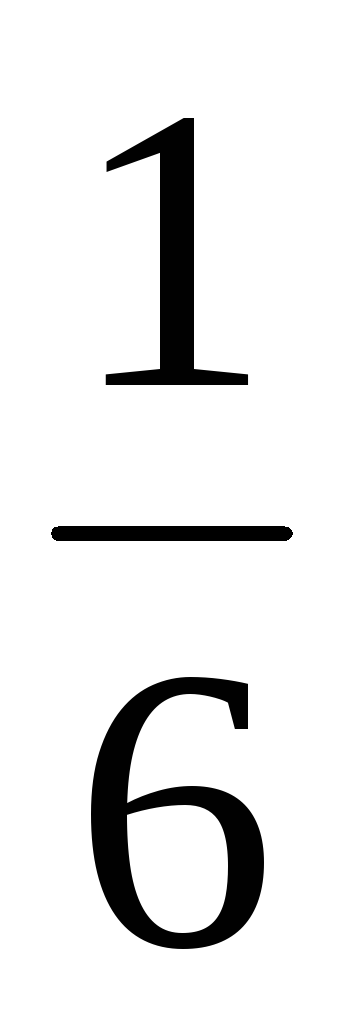
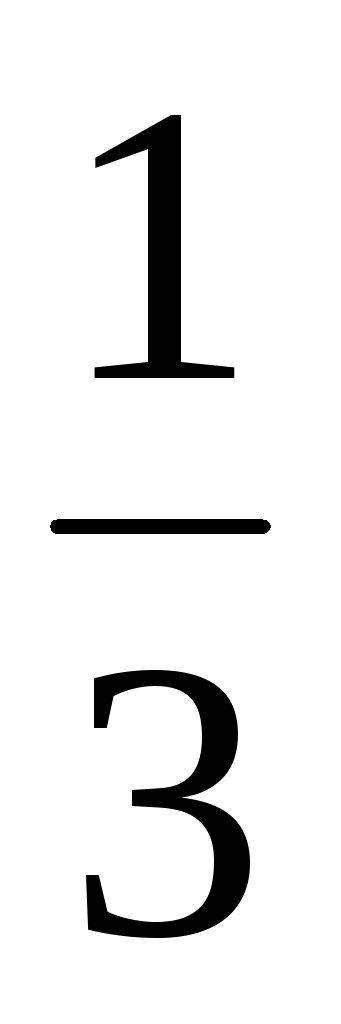
Вероятности вычисляются следующим образом:

,

и т.д.

По таблице распределения вероятностей системы случайной величин , можно составить законы распределения случайных величин, входящих в систему.

1 2 3

1 2 3

.

.

.

.

.

.

.

.

;

.

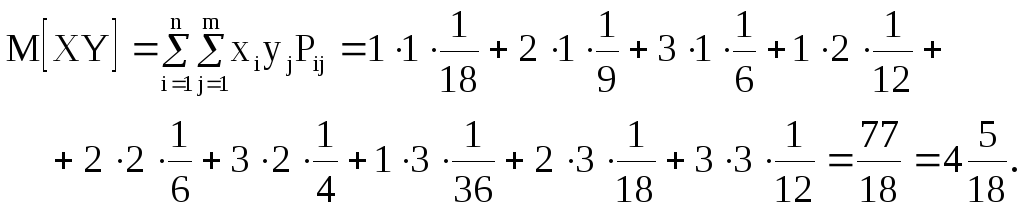
Этот результат можно было предвидеть, так как независимы из условия.

2.Дана плотность распределения вероятностей системы случайных величин

.

Определить функцию совместного распределения системы , математические ожидания, дисперсии, корреляционную матрицу.

Решение.

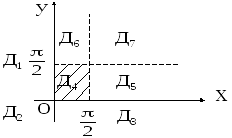
Определим функцию , рассматривая области.

.

.

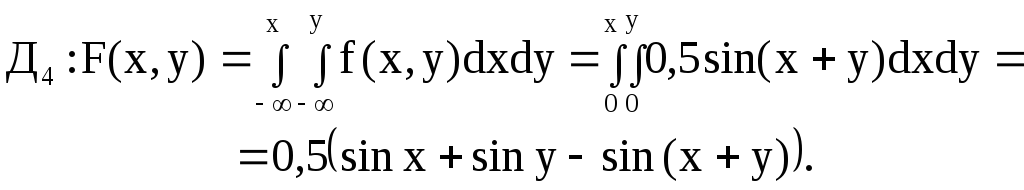
Таким образом,

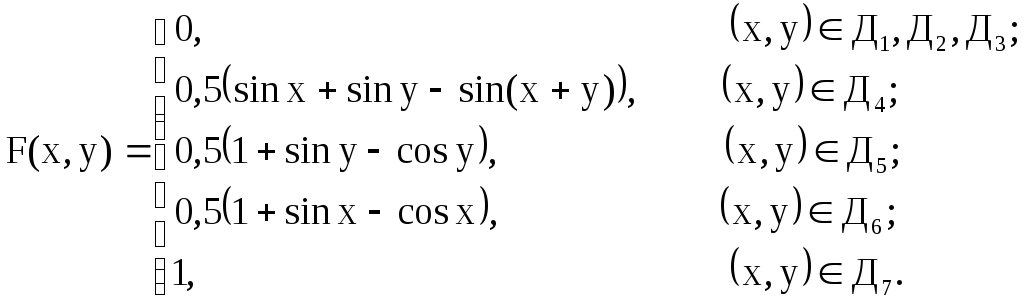
Найдем математические ожидания случайных величин, входящих в систему

.

.

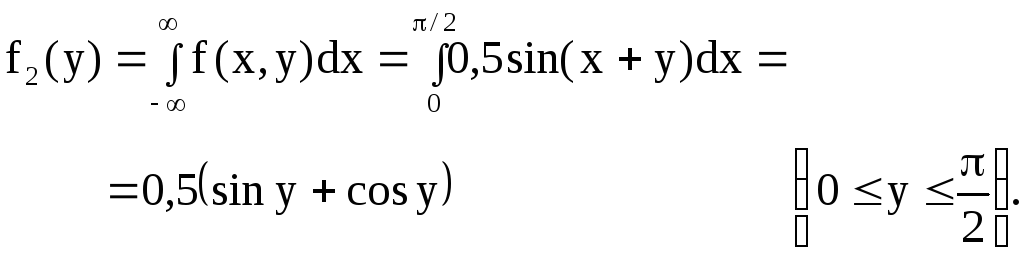
Для составления корреляционной матрицы найдем

.

.

.

.

.

.

3. Определить в точке плотность распределения вероятностей системы двух нормально распределенных случайных величин, для которых

.

.

Решение. Так как и случайные величиныраспределены по нормальному закону, то случайные величинынезависимы и, следовательно,

.

,

,

,

.
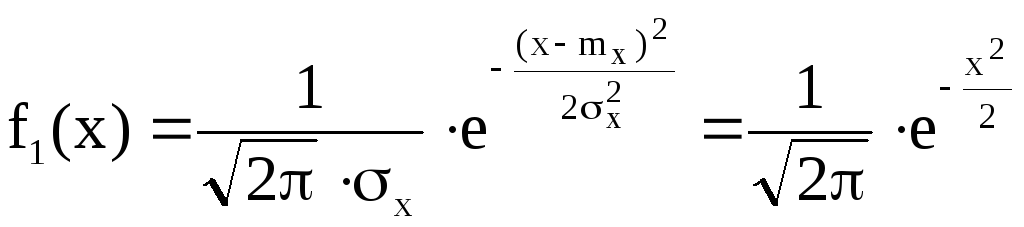
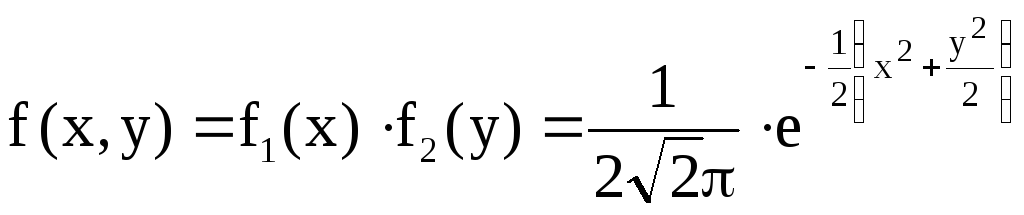