7. Примеры распределения случайных величин

Дискретная случайная величина называется распределенной побиномиальному закону, если ее возможные значения 0, 1, …, n , а вероятность того, что , выражается формулой

,

где .

Математическое ожидание случайной величины , распределенной по биномиальному закону, равно, а дисперсия.

Дискретная случайная величина называется распределенной по законуПуассона, если ее возможные значения 0, 1, …, m, …, а вероятность того, что выражается формулой

,

где - параметр закона Пуассона.

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру .

Непрерывная случайная величина называетсяравномерно распределенной в интервале , если ее плотность распределения в этом интервале постоянна.

Математическое ожидание и дисперсия случайной величины, распределенной равномерно на участке , равны соответственно

.

Непрерывная случайная величина называется распределенной попоказательному закону, если ее плотность распределения

где - параметр показательного закона.

Для случайной величины , распределенной по показательному закону,

.

Функция распределения имеет вид

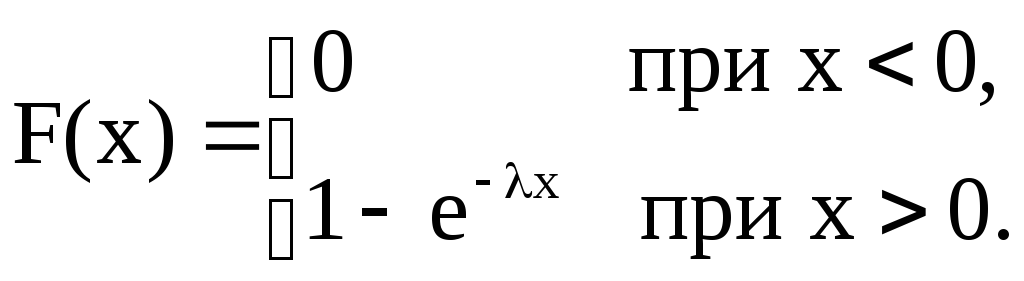
Непрерывная случайная величина называется распределенной понормальному закону, если ее плотность распределения

.

Математическое ожидание случайной величины , распределенной по нормальному закону, равно, а дисперсия.

Вероятность попадания случайной величины , распределенной по нормальному закону, в интервалравна

,

где - табулирована,

отсюда .

Типовые задачи для решения в аудитории

1. Стрелок делает по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий и вычислить математическое ожидание и дисперсию указанной случайной величины.

Решение. Случайная величина - число попаданий в мишень при 3-х выстрелах, распределена по биномиальному закону, ее возможные значения 0, 1, 2, 3.

;

;

;

.

Ряд распределения случайной величины :

	0	1	2	3
	0,343	0,441	0,189	0,027

; .

2. Длина заготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами ,. Найти вероятность брака, если допускаемые размеры детали должны быть. Какую точность длины можно гарантировать с вероятностью 0,97?

Решение. а) .

.

Вероятность брака .

б)

.

Следовательно, с вероятностью 0,97 можно гарантировать размеры .

3. Снайпер стреляет по замаскированному противнику до первого попадания. Вероятность промаха при отдельном выстреле равна . Найти математическое ожидание числа промахов.

Решение. Возможные значения случайной величины - числа промахов:.

Ряд распределения случайной величины :

	0	1	2	…	k	…
				…		…

Полученное распределение носит название геометрического распределения.

.

Для вычисления суммы полученного ряда рассмотрим ряд

.

Отсюда .