5. Последовательность независимых испытаний (схема Бернулли). Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа

Вероятность появления событияраз внезависимых испытаниях (опытах), в каждом из которых вероятность появления события равна, определяетсяформулой Бернулли: , где.

Вероятность появления события не менее раз виспытаниях вычисляется по формуле

или .

Вероятность появления события хотя бы один раз в испытаниях будет.

Наивероятнейшее число появлений события внезависимых испытаниях.

Теорема Пуассона. Вероятность того, что в независимых испытаниях в

каждом из которых вероятность появления события равна , событие наступит ровнораз при достаточно большоми малом

приближенно равна ,

где .

Локальная теорема Муавра-Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна, событие наступит ровнораз при достаточно большомприближенно равна

,

где .

Интегральная теорема Муавра-Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна, событие наступит не менеераз и не болеераз при достаточно большомприближенно равна

,

где 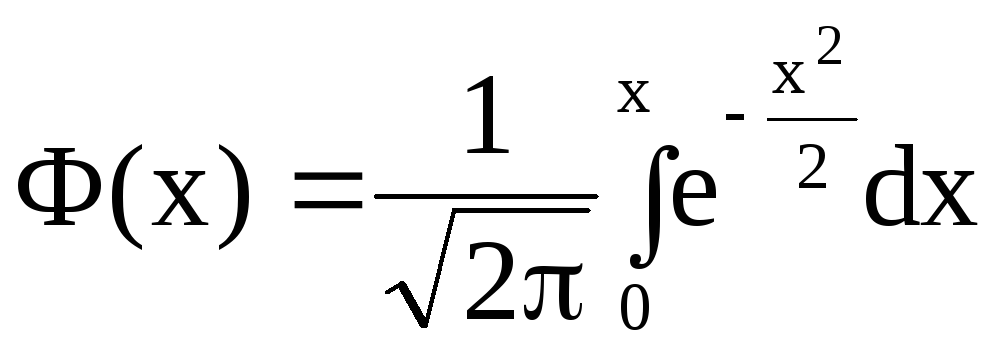- функция Лапласа,

.

Типовые задачи для решения в аудитории

1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен) : а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми?

Решение. Так как противники равносильны, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны .

а) Вероятность выиграть три партии из четырех

.

Вероятность выиграть пять партий из восьми

.

Так как , то вероятнее выиграть три партии из четырех.

б) Вероятность выиграть не менее трех партий из четырех

,

а вероятность выиграть не менее пяти партий из восьми

Так как , вероятнее выиграть не менее пяти партий из восьми.

2. Из таблицы случайных чисел наудачу выписаны 200 двузначных случайных чисел (от 0 до 99). Определить вероятность того, что среди них число 33 встретиться: а) три раза; б) четыре раза.

Решение. Вероятность того, что наудачу выбранное двузначное число равно 33, равна , поскольку выбирается одно из 100 возможных. Число испытаний. Так как числовелико, а вероятностьмала, воспользуемся формулой Пуассона:

,

где .

а) ; б).

3. Вероятность появления события при одном опыте равна 0,3. С какой вероятностью можно утверждать, что частота этого события при 100 опытах будет лежать в пределах от 0,2 до 0,4?

Решение. Для того чтобы частота лежала в пределах от 0,2 до 0,4 в серии из 100 опытов, число появлений события должно быть не менее 20 и не более 40.

Воспользуемся интегральной теоремой Муавра-Лапласа:

.

По условию , следовательно:

,

.