
4. Термодинамические процессы идеального газа
4.1. Метод исследования процессов
Метод исследования процессов является общим, не зависящим от особенностей того или иного процесса, и состоит в следующем.
1. На основании рассмотрения условий, при которых осуществляется процесс, выводится уравнение процесса.
2. В системе координат p, u строится график процесса.
3. Выводятся формулы зависимостей между параметрами вида: p=f1(u); T=f2(u); T=f3(p).
4. Определяется изменение внутренней энергии рабочего тела по общей для всех процессов формуле du = cudT.
5.
Определяется работа изменения объема
по выражению
 и техническая работа по формуле
и техническая работа по формуле .
.
6. Определяется количество тепла, участвующего в процессе, по уравнениям q = Du + l или q = c(T2 - T1), где с - теплоемкость в данном процессе.
7. Определяется изменение энтропии в процессе и строится график процесса в Т, s - координатах.
Практический интерес представляют следующие термодинамические процессы:
1) изохорный (u = const);
2) изобарный ( р = const);
3) изотермический (Т = const);
4) адиабатический (dq = 0);

4.2. Изохорный, изобарный, изотермический процессы
Изохорный процесс. Процессы, протекающие при постоянном объеме рабочего тела, называются изохорными процессами. Линию, изображающую изохорный процесс (рис. 4.1), называют изохорой. Уравнение изохорного процесса в координатах p, u
u = const или du = 0.
График процесса в координатах p, u: вертикаль 1-2 или 1-3. 1-2 - подвод теплоты, 1-3 - отвод теплоты.
Зависимость между параметрами получим из уравнений состояния для состояний 1 и 2:
p2u = RT2 и p1u = RT1.
Относя эти уравнения друг к другу, получим
![]() .
(4.1)
.
(4.1)
Уравнение (4.1) представляет собой закон Шарля, согласно которому: в изохорном процессе отношение давлений прямо пропорционально отношению абсолютных температур.
Изменение
внутренней энергии Du
= u2
- u1
= cu(T2
- T1).
Работа изменения объема
 ,
т.к. du=
0. Техническая работа в процессе 1-2
,
т.к. du=
0. Техническая работа в процессе 1-2
 ,
в процессе 1-3
,
в процессе 1-3 .
Количество тепла qu
=
Du
= cu(T2
- T1),
т.к. l
= 0, т.е. в изохорном процессе все тепло,
сообщаемое рабочему телу, идет на
увеличение его внутренней энергии.
.
Количество тепла qu
=
Du
= cu(T2
- T1),
т.к. l
= 0, т.е. в изохорном процессе все тепло,
сообщаемое рабочему телу, идет на
увеличение его внутренней энергии.
Изменение энтропии в процессе найдем по уравнению второго закона термодинамики:
![]() (4.2)
(4.2)
или
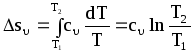 .
(4.3)
.
(4.3)

Вид и особенности изохоры могут быть установлены при рассмотрении ее углового коэффициента
![]() .
.
Из
уравнения (4.2) получим
![]() ,
откуда
,
откуда![]() .(4.4)
.(4.4)
Как видим из уравнения (4.4), угловой коэффициент изохоры возрастает по мере увеличения температуры газа. Это значит, что изохора своей выпуклостью обращена в сторону оси абсцисс.
Изобарный процесс. Процессы, протекающие при постоянном давлении рабочего тела, называются изобарными процессами. Линия, изображающая изобарный процесс, называется изобарой. Уравнение изобарного процесса в координатах p, u
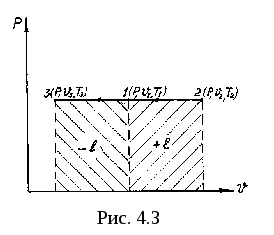
График процесса (рис. 4.3) - горизонталь 1-2 или 1-3. 1-2 - расширение (подвод тепла), 1-3 - сжатие (отвод тепла). Найдем соотношение параметров. Относя уравнение состояния pu2 = RT2 к pu1 = RT1 , получим
![]() .
(4.5)
.
(4.5)
Уравнение (4.5) представляет закон Гей-Люссака, согласно которому: в изобарном процессе отношение объемов газа прямо пропорционально отношению абсолютных температур.
Изменение внутренней энергии Du = cu(T2 -T1).
Работа изменения объема
 .
.
Техническая
работа
 ,
т.к. dp = 0.
,
т.к. dp = 0.
Количество тепла, участвующего в процессе:
qp = cp (T2 - T1) = h2 - h1 . (4.6)
Равенство (4.6) вытекает из уравнения (2.23). Следовательно, в изобарном процессе количество подведенного или отведенного тепла равно изменению энтальпии рабочего тела.
Изменение
энтропии
![]() (4.7)
(4.7)
или
в интегральной форме
 .
(4.8)
.
(4.8)
Это уравнение показывает, что изобара в осях T, s будет логарифмической кривой, направленной выпуклостью вниз (рис. 4.4).

1-3- отвод тепла (сжатие).
Угловой коэффициент изобары (по аналогии с изохорой)
![]() .
.
Сравнение угловых коэффициентов изохоры и изобары
![]() и
и
![]() показывает, что изобары являются более
пологими кривыми, чем изохоры, т.к. cp
> cu.
показывает, что изобары являются более
пологими кривыми, чем изохоры, т.к. cp
> cu.
Изотермический процесс. Процессы, протекающие при постоянной температуре рабочего тела, называются изотермическими процессами. Линия, изображающая изотермический процесс, называется изотермой. Условие совершения изотермического процесса Т = const или dT = 0.
Уравнение изотермического процесса в осях P, u может быть получено из уравнения состояния Pu = RT = const. Т.к. T = const и R = const для данного газа, то получаем
Pu = const. (4.9)
Уравнение изотермы (4.9) выражает закон Бойля-Мариотта, согласно которому: при постоянной температуре отношение объемов рабочего тела обратно пропорционально отношению давлений.
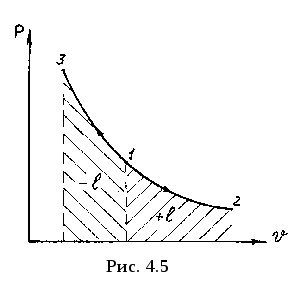
1-2- расширение (подвод тепла), 1-3-сжатие (отвод тепла). Из уравнения изотермы (4.9) получаем связь между параметрами:
![]() .
(4.10)
.
(4.10)
Изменение внутренней энергии
du = cudT = 0, т.к. dT = 0.
Вследствие этого изменение энтальпии также равно нулю:
dh = cpdT = 0 и Dh = 0.
Работа изменения объема найдется по выражению
 .
(4.11)
.
(4.11)
Техническая работа
 .
(4.12)
.
(4.12)
Следовательно, в изотермическом процессе l = l¢.
Так как Du = 0, то, согласно первому закону термодинамики:
qт = lт,
тогда
![]() .
(4.13)
.
(4.13)
Если говорить о теплоемкости в изотермическом процессе, то надо полагать, что ст = ¥, т.к. при подводе тепла температура рабочего тела не меняется.

1-2 - расширение (подвод тепла), 1-3 - сжатие (отвод тепла).
Изменение энтропии найдется по выражению
 (4.14)
(4.14)
Откуда q = TDsт (4.15)
