§4. Формула полной вероятности. Формула Байеса

Вероятность Р(А) появления события А, которое может произойти только совместно с одним из событий , образующих полную группу несовместных событий (гипотез), определяется формулой полной вероятности

.

Вероятность гипотезыпосле того, как имело место событиеА, определяется формулой

Пример 1. В торговую фирму поступили телевизоры от трех поставщиков, в отношении 1:4:5. Известно, что телевизоры, поступающие от 1-го, 2-го, 3-го поставщиков не требуют ремонта в течение гарантийного срока соответственно в 98; 88 и 92 % случаев.

а) Найти вероятность того, что поступивший в продажу телевизор не потребует ремонта в течение гарантийного срока.

б) Телевизор сломался. От какого поставщика вероятнее всего он поступил?

Решение. Пусть А – телевизор не сломается в течение гарантийного срока, ­– телевизор поступил в продажу отi-го поставщика. Тогда

По формуле полной вероятности получим:

а)

б) т.к. телевизор сломался, то

И по формуле Байеса получим

То есть, скорее всего, он поступил от второго поставщика.

§5. Повторные независимые испытания

Вероятность появления событияраз в серии изнезависимых опытов, в каждом из которых вероятность появления события равна, определяется формулой биноминального распределения

.

Вероятность появления события хотя бы один раз при опытах будет

.

Количество опытов, которые нужно произвести для того, чтобы с вероятностью не меньшеможно было утверждать что данное событие произойдет по крайней мере один раз, находится по формуле:

где – вероятность появления события в каждом опыте.

Число называется наивероятнейшим числом наступлений событияА, если для всех m = 0,1,…,. Это число определяется по формуле

.

Пример 1. Игральную кость подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет 2 раза.

Решение. Здесь ;;;;

.

Пример 2. Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти наиболее вероятное число опоздавших из 96 студентов.

Решение. Имеем n = 96; р = 0,08; q = 0,92,

Если число испытаний достаточно велико, а вероятностьдостаточно мала, причем их произведениеа = np стремится к постоянному числу , то вероятностьможно приближенно найти по формуле Пуассона

.

Если число испытаний достаточно велико, а вероятностииq не очень близки к нулю , то вероятностьможно приближенно найти по локальной формуле Муавра – Лапласа

,

где ; – функция Гаусса, она табулирована,

.

В условиях локальной формулы Муавра – Лапласа вероятность того, что число успеховзаключено междуи, можно приближенно найти по интегральной формуле Муавра – Лапласа

,

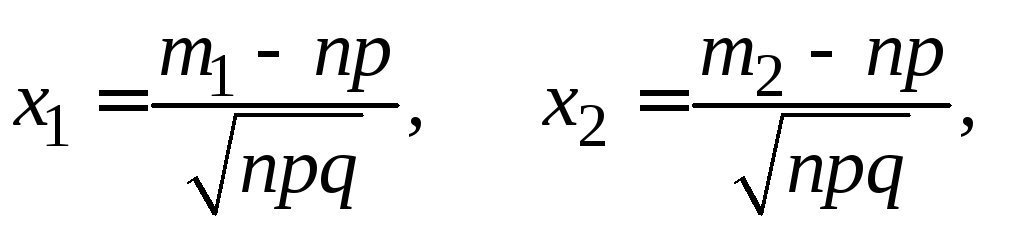
где – функция Лапласа, она табулирована, .

Пример 3. На факультете насчитывается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно для 2-х студентов?

Решение. Имеем n = 500; ,q = 0,9973. Так как , то воспользуемся формулой Пуассона

.

Пример 4. Вероятность брака при изготовлении деталей постоянна и равна 0,05. Какова вероятность, что в партии из 1000 изделий встретится равно 40 бракованных.

Решение. По условию задачи n = 1000, m = 40; p = 0,05; q = 0,95. Кроме того: Поэтому воспользуемся локальной формулой Муавра – Лапласа

Пример 5. Фабрика выпускает 70 % продукции первого сорта. Чему равна вероятность того, что в партии из 1000 изделий число изделий первого сорта будет заключено между 652 и 760?

Решение. По условию имеем: n = 1000, p = 0,7, q = 0,3, = 652,= 760. Искомую вероятность найдем по интегральной формуле Муавра – Лапласа

Если в некоторой серии из n испытаний событие А наступает m раз, то частота его появления . Тогда неравенстворавносильно неравенствам, и из интегральной теоремы Муавра-Лапласа следует

.

Пример 6. Сколько раз надо подбросить симметричную монету, чтобы с вероятностью 0,9 частота появления герба отличалась отне более чем на 0,01?

Решение. Подставим значения в формулу