
Bescennaya_i_dr.Grafiki_funkcii
.pdf
где х, у – декартовы координаты произвольной точки М(х,у), а ρ,ϕ - её полярные координаты.
Здесь декартова система координат выбрана так, чтобы её начало О совпадало с полюсом полярной системы, а ось ОХ – с полярной осью.
Элементарные функции и их графики
Основными элементарными функциями называются следующие: - степенная функция у = хα , где a Î R ;
- показательная функция y = a x , где a > 0, a ¹ 1;
- логарифмическая функция y = loga x, где a > 0, a ¹ 1;
- тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x ; -обратные тригонометрические функции: y = arcsin x , y = arccos x, y = arctg x,
y = arcctg x .
Элементарными функциями являются основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложение, вычитание, умножение, деление) и суперпозиции, например:
у = 
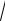 1 + 2сos3 x , y = 52x + log2 x . 5
1 + 2сos3 x , y = 52x + log2 x . 5  x + 3ctgx
x + 3ctgx
Назовем некоторые классы элементарных функций.
Целая рациональная функция, или многочлен y = a 0 x n + a1x n+1 + ... + a n , где n-
целое неотрицательное число (степень многочлена), а0 , а1 ,..., аn - постоянные числа (коэффициенты).
Дробно-рациональная функция, которая является отношением двух целых рациональных функций:
y = |
a |
0 |
x n + a |
x n−1 + ... + a |
n |
|
|
1 |
|
. |
|||
|
|
|
|
|
||
|
b0 x m + b1x m−1 + ... + bm |
|||||
Целые рациональные и дробно-рациональные функции образуют класс
рациональных функций.
Иррациональная функция – это та, которая изображается с помощью суперпозиций рациональных функций и степенных функций с рациональными целыми показателями, например:
11
y = 3 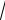 2x 2 + 1 + x3 ; y =
2x 2 + 1 + x3 ; y = 
 x + 2 . 5
x + 2 . 5  2 + 3x − 27
2 + 3x − 27
Рациональные и иррациональные функции образуют класс алгебраических функций.
2. |
СПРАВОЧНЫЙ МАТЕРИАЛ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Степенная функция |
|
|
|
|
|
|
|
||||
|
|
Y |
|
|
|
|
Y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
(1;1) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
X |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 2.1. y = |
1 |
|
|
|
Рис. 2.2. |
y = |
1 |
|
||||||||||
x 2n |
x3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
(1,1) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
X |
|||||
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||
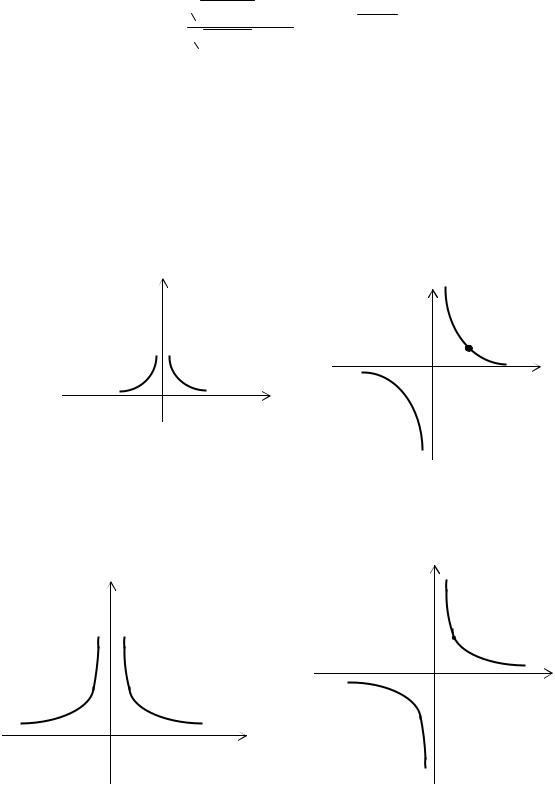
Рис. 2.3. y = |
1 |
|
|
|
|
|
|
|
Рис. 2.4. y = |
1 |
|
|
|
|
|
|
|||
x 2 |
|
x 2n+1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
12
Y Y
0 |
x |
0 |
x |
Рис. 2.5. Обратно |
пропорциональная |
Рис. 2.6. Обратно пропорциональная |
||||
зависимость |
y = |
k |
, k > 0 |
зависимость y = |
k |
, k < 0 |
|
|
|||||
|
|
x |
|
x |
||
Y |
|
|
|
Y |
|
|
|
|
|
||||||
(1;1) |
|
|
|
|
|
|
(1;1) |
|
|
||||||
0 |
|
|
|
|
|
x |
0 |
|
|
x |
|||||
а |
|
|
|
|
|
|
|
б |
|
||||||
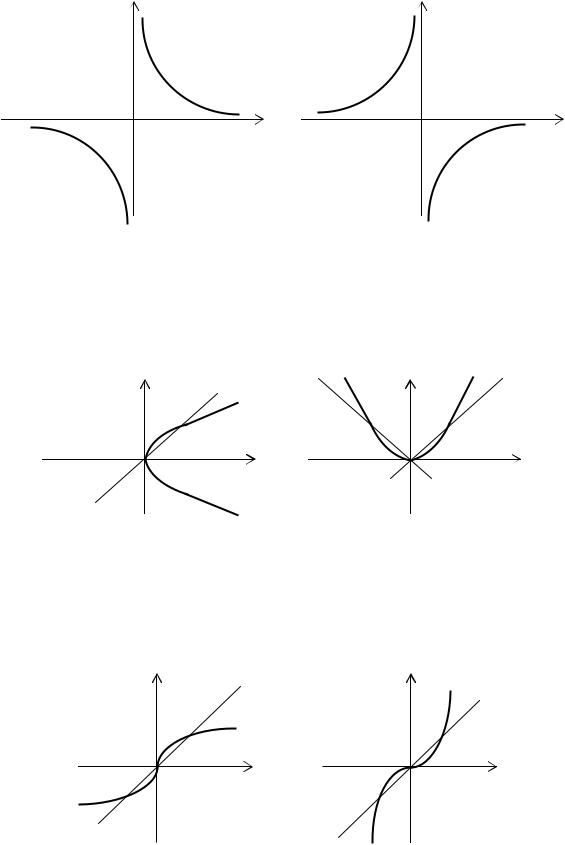
Рис. 2.7. Степенная функция с положительным рациональным |
|
||||||||||||||
показателем y = x |
p |
p − четное, q − нечетное: |
p |
< 1 (a); |
p |
> 1 (б) |
|
||||||||
|
, |
|
|||||||||||||
q |
|
||||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
q |
|
|
q |
|
||
Y |
|
|
|
Y |
|
|
|
|
|
||||||
(1;1) |
|
|
|
|
|
(1;1) |
|
|
|||||||
0 |
|
|
|
|
x |
0 |
|
|
|
x |
|
||||
а |
|
|
|
|
б |
|
|||||||||
Рис. 2.8. Степенная функция с положительным рациональным |
|
||||||||||||||
показателем y = x |
p |
и q − нечетные: |
p |
< 1 (a), |
p |
> 1 (б) |
|
||||||||
|
, p |
|
|||||||||||||
q |
|
||||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
q |
q |
|
||||||
13
Y Y
|
(1;1) |
|
(1;1) |
0 |
x |
0 |
x |
а |
|
|
|
|
б |
||
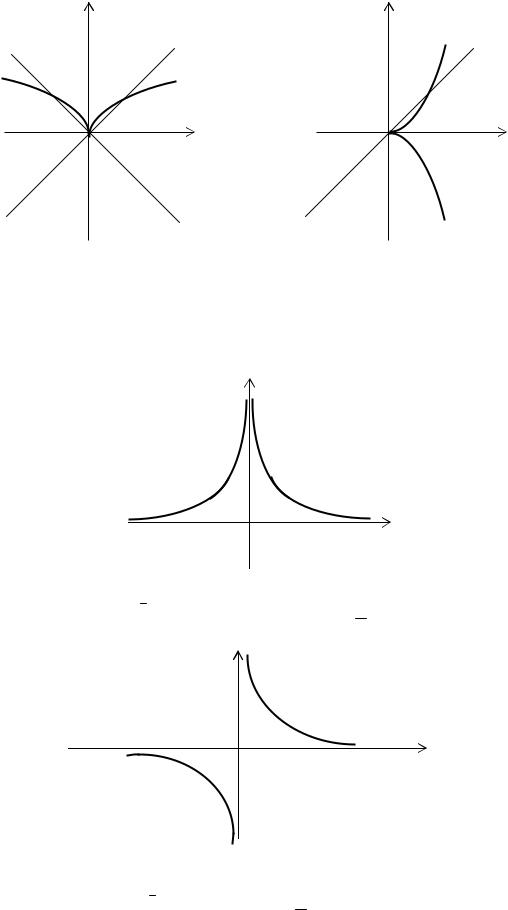
Рис. 2.9. Степенная функция с положительным рациональным |
|||||||
|
|
p |
|
|
|
||
|
y = x |
|
, p − нечетное, q − четное: |
p |
< 1 (a); |
p |
> 1 (б) |
показателем |
q |
||||||
|
q |
|
|||||
|
|
|
|
|
q |
||
Y
0 х
Рис. 2.10. Степенная функция с отрицательным рациональным
показателем y = x − p , p − четное, q − нечетное; p > 0
q
q
Y
0 |
x |
Рис. 2.11. Степенная
− p
показателем y = x q
функция с отрицательным рациональным
, p, q − нечетные; p > 0 q
14
Y
0 |
x |
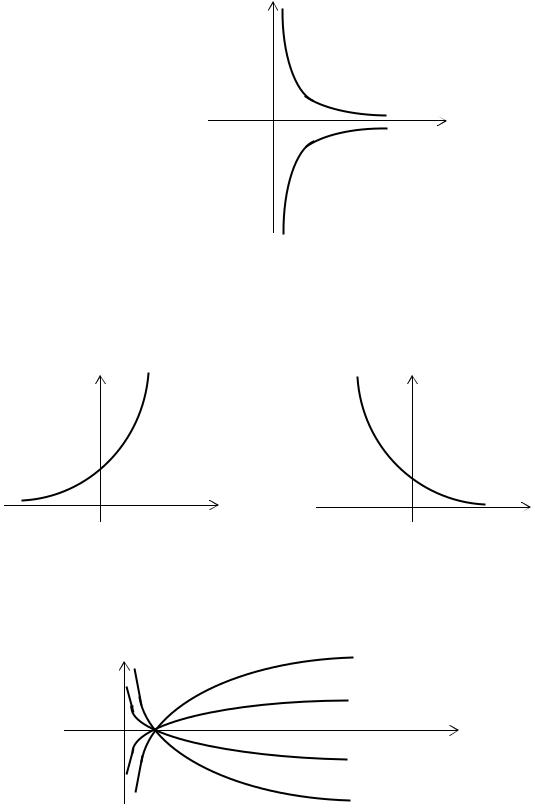
Рис. 2.12. Степенная функция с отрицательным
|
− |
p |
|
p |
|
|
|
|
|||||
рациональным показателем |
y = x q , p − нечетное, q − четное; |
> 0 |
||||
|
||||||
|
|
|
|
q |
||
Y |
|
|
Y |
|||
|
(0;1) |
(0;1) |
|
0 |
x |
0 |
x |
|
а |
|
б |
Рис. 2.13. Показательная функция y = a x : a > 1 (а); |
а < 1 (б) |
||
Y |
2 |
|
1 |
0 |
x |
|
3 |
|
4 |
Рис. 2.14. Логарифмическая функция y = loga x, a > 0 : a = 10 (1); a = e (2);
a = |
1 |
(3); a = |
1 |
(4) |
|
e |
|||
10 |
|
|
||
15
Y
|
|
|
|
|
|
|
|
|
-3π/2 |
-π/2 |
0 π/2 |
3π/2 |
x |
||||
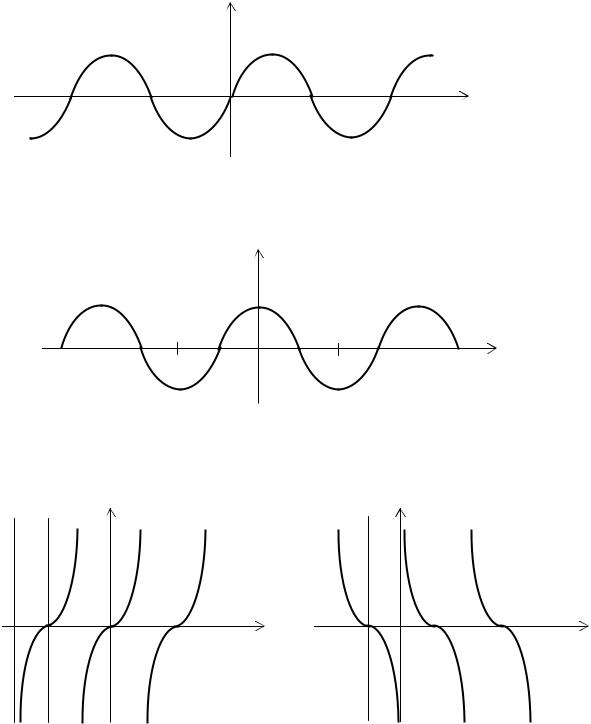
Рис. 2.15. Тригонометрическая функция |
y = sin x |
|||||||
Y
-3π/2 |
π/2 |
π/2 |
3π/2 |
|
0 |
|
x |
Рис. 2.16. Тригонометрическая функция y = cos x
Y Y
|
-π |
-π/2 |
|
π/2 |
|
π |
|
-π |
-π/2 |
|
π/2 |
π |
|
3π/2 |
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
|
x |
0 |
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.17. Тригонометрическая |
Рис. 2.18. Тригонометрическая |
функция y = tg x |
функция y = ctg x |
16
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
3π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
x |
|
|||
-1 |
0 1 |
x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
-π/2 |
|
|
|
|
|
|
|
-π/2 |
|
|
|
|
|
|
|
|
-π |
|
|
|
|
|
|
|
|
|
|
|
|
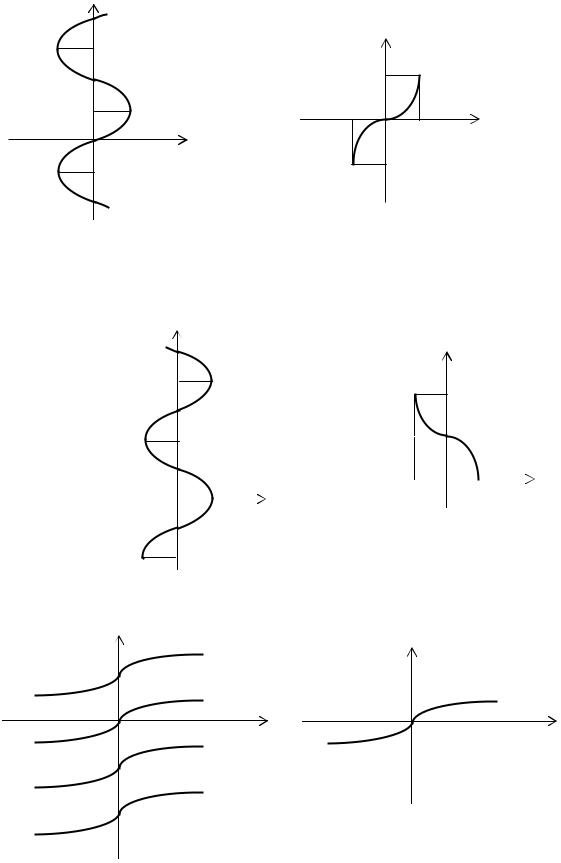
Рис. 2.19. Обратная тригономет- |
|
|
|
|
Рис. 2.20. Обратная тригонометри- |
|||||||||||
рическая функция y = Arcsin x |
|
|
|
|
ческая функция y = arcsin x |
|
||||||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5π/2 |
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
3π/2 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
|
x |
|
|
|
|
-1 0 |
1 |
|
|
x |
|
|
|
|
|
|||
|
|
|
|
-π |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.21. Обратная тригонометрическая |
Рис. 2.22. Обратная тригонометри- |
|||||||||||||||
функция |
y = Arccos x |
|
|
|
|
|
|
|
ческая функция y = arccos x |
|||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-π |
|
|
|
|
|
|
|
-π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Рис. 2.23. Обратная тригонометри- |
Рис. 2.24. Обратная тригонометри- |
|||||||||||||||
ческая функция |
y = Arctg x |
|
|
|
|
|
|
|
ческая функция |
y = arctg x |
||||||
17
Y
 5π/2
5π/2
|
3π/2 |
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
π/2 |
||
|
|
|
|
|
|
||
0 |
x |
|
|
||||
|
-π/2 |
0 |
|
x |
|||
|
|
|
|
|
|
|
|
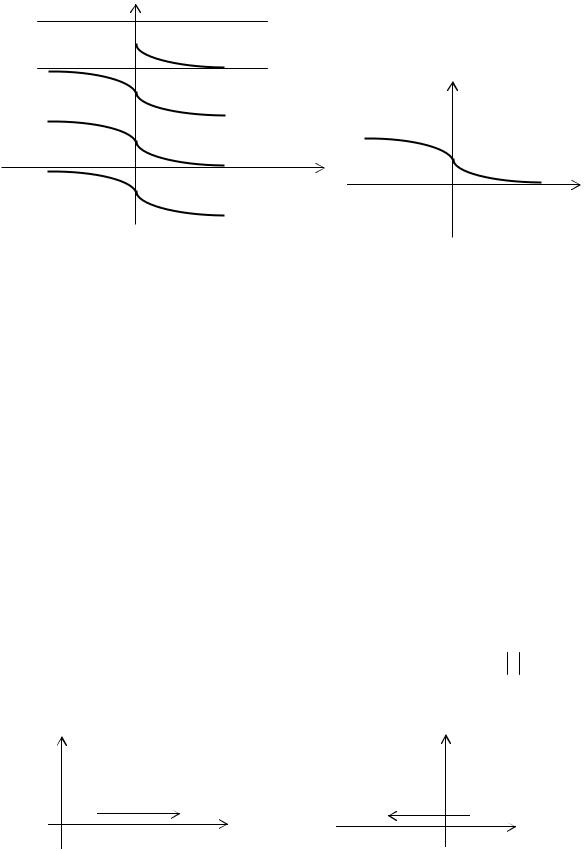
Рис. 2.25. Обратная тригонометри- |
Рис. 2.26. Обратная тригонометрическая |
ческая функция y = Arcctg x |
функция y = arcctg x |
3. УКАЗАНИЯ К ВЫПОЛНЕНИЮ ТИПОВОГО РАСЧЕТА Задача 1.
По графику функции y = f (x) путем сдвигов и деформаций построить график функции y =A × f (kx + m) + B .
Построение заданной функции проводится в несколько этапов, которые мы здесь рассмотрим. Функцию y = f (x) будем называть основной.
Построение графика функции y = f (x − а) .
Предположим, что для некоторых x1 и x2 основная и заданная функции имеют
равные ординаты, то есть f (x1 ) = f (x 2 |
- a ). Но тогда должно быть x1 = x 2 - a и |
x 2 = x1 + a . В зависимости от знака a |
возможны два случая. |
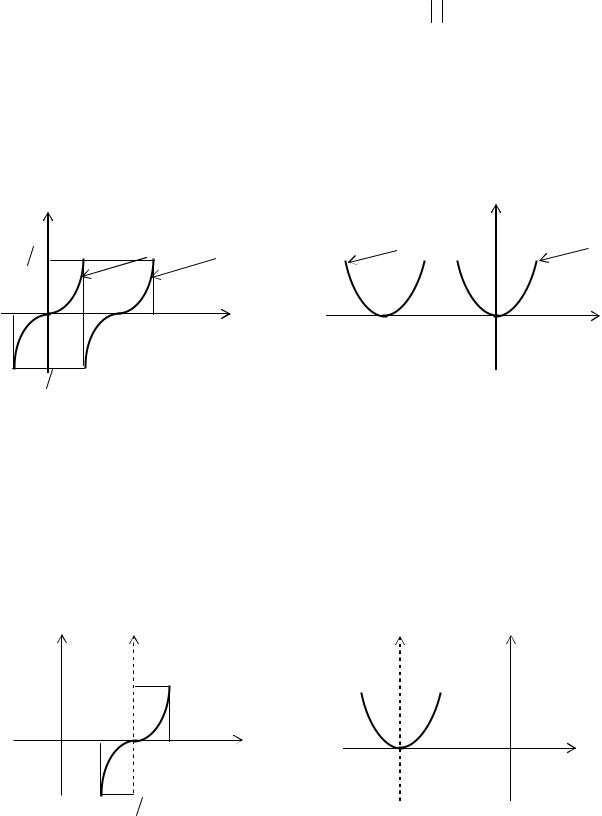
1. Если a > 0, то точка M(x + a; y) графика функции y = f (x − а) смещена вдоль оси OX на a единиц вправо по сравнению с точкой N(x,y) графика функции f(x) (рис. 3.1).
2. Если a < 0, то точка M(x + a; y) смещена вдоль оси OX на a единиц влево по
сравнению с точкой N(x,y) графика функции f(x) (рис. 3.2). Таким образом получаем
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
N(x; y) |
M(x+a; y) |
M(x+a; y) |
|
y |
N(x; y) |
|
||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
x+a |
x |
x+a |
0 |
x |
x |
||||||
|
|
Рис. 3.1 |
|
|
|
|
Рис. 3.2 |
|
|||||
18
Правило 1. Если a > 0, то график функции f(x-a) получается из графика основной функции f(x) путем его параллельного переноса вдоль оси OX на “a” единиц вправо.
Если a < 0, то график функции f(x-a) получается из графика основной функции f(x) путем его параллельного переноса вдоль оси OX на a единиц влево.
Примеры. Построить графики функций: 1) y = arcsin (x − 2); 2) y = (x + 3)2 .
1) Здесь a = 2 > 0. Строим график функции y = arcsin x . Сдвинув его на 2 единицы вправо вдоль оси OX, получим график функции y = arcsin (x − 2)
(рис. 3.3).
2) Здесь a = -3 < 0. Строим график функции y = x 2 . Сдвинув его на 3 единицы
влево, получим график функции y = (x + 3)2 |
(рис. 3.4). |
|
Y |
|
Y |
y = arcsin x y = arcsin (x − 2) |
y=(x+3)2 |
y=x2 |
π 2 |
|
|
-1 0 1 2 3 |
x |
-3 -2 -1 0 |
1 2 |
x |
||||
− π 2 |
|
|
|
|
|
|
|
|
Рис. 3.3 |
|
|
|
Рис. 3.4 |
|
|
||
Замечание. Построение |
графика |
функции у = f (x − a ) можно выполнить |
||||||
иначе: построив график основной функции y1 = f (x ) в системе |
XO1Y1 , |
надо |
||||||
перенести ось O1Y1 , на а единиц влево, если а > 0 , и на |
|
a |
|
единиц вправо, |
если |
|||
|
|
|||||||
а < 0 . Тогда в системе XOY получим график функции y = f (x − a ). Система XO1Y1 имеет вспомогательное значение, поэтому ось O1Y1 изображается пунктирно или карандашом.
В качестве примера построим еще раз графики функций y = arcsin(x − 2) и y = (x + 3)2 (рис. 3.5) и (рис. 3.6)
Y |
Y1 |
Y1 |
Y |
π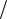 2
2
|
|
|
О1 |
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
||
0 1 |
2 |
x |
-3 |
-2 |
|
-1 |
|
0 |
x |
|
|
||||||||
|
− π 2 |
|
|
|
|
|
|
|
|
|
Рис. 3.5 |
|
|
Рис. 3.6 |
|
||||
19
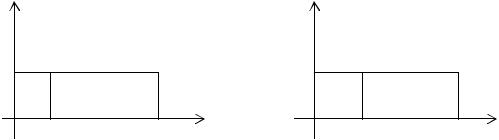
Построение графика функции y = f (kx ), где k > 0. |
|
|
|
|
||||||||||
Пусть для некоторых значений x1 |
и |
x 2 |
ординаты функций f (x ) и f (kx) равны, |
|||||||||||
то есть |
f (x1 ) = f (kx 2 ). Тогда |
x1 = kx 2 |
|
и |
x 2 = |
x1 |
. Таким образом, каждой точке |
|||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
k |
|
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
N(x, y) |
графика основной функции |
f (x ) соответствует точка М |
|
; y графика |
||||||||||
|
||||||||||||||
функции f (kx ). Возможны два случая. |
|
|
|
|
|
k |
|
|||||||
|
|
|
|
|
|
|
|
|||||||
1. Если k > 1, то точка |
M |
x |
; y |
лежит в k раз ближе к оси OY, чем точка |
||||||||||
|
||||||||||||||
N(x; y) |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 3.7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
||
2. Если же 0 < k < 1, то точка |
M |
|
; y |
лежит в |
|
раз дальше от оси OY по |
||||||||
|
|
|||||||||||||
|
|
|
|
k |
|
|
|
|
k |
|
||||
сравнению с точкой N(x; y) (рис. 3.8). Таким образом, происходит сжатие или растяжение графика функции.
Y |
|
Y |
|
|
|
|
x |
|
|
x |
|
||
y M |
|
; y N(x; y) |
y N(x; y) |
M |
|
; y |
|
|
|||||
k |
|
|
k |
|
||
|
x |
|
|
|
|
x |
||
0 |
|
x |
X |
0 |
x |
|
|
X |
|
|
|||||||
|
k |
|
|
|
|
k |
||
|
|
Рис. 3.7 |
|
|
|
Рис. 3.8 |
||
Правило 2. Пусть k > 1. Тогда график функции |
f(kx) получается из графика |
|||||||
функции f(x) путем его сжатия вдоль оси OX в k раз (иначе: его сжатием к оси OY в k раз).
Пусть 0 < k < 1. Тогда график f(kx) получается из графика f(x) путем его
растяжения вдоль оси OX в |
1 |
раз. |
||||||
k |
||||||||
|
|
|
|
|
x |
|
||
Примеры. |
Построить графики функций: 1) y = arccos 2x и y = arccos |
; |
||||||
|
||||||||
|
|
x |
|
|
2 |
|
||
2) y = sin 2x и |
y = sin |
. |
|
|
|
|||
|
|
|
|
|||||
|
2 |
|
|
|
|
|
||
20
