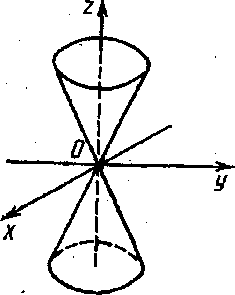
3. Конус второго порядка (рис. 25). Каноническое уравнение конуса имеет вид

Поверхности, заданные уравнениями

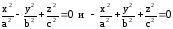, также определяют конические поверхности, только иначе расположены относительно системы координат.

Рис. 25

4. Параболоиды. Каноническое уравнение параболоида имеет вид

Эллиптический параболоид (рис. 26) определяется уравнением

, а гиперболический (рис. 27) – уравнением .

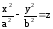Рис. 26 Рис. 27

Поверхности, заданные в декартовой системе координат уравнением

или ,

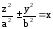также определяют эллиптический и гиперболический параболоиды, иначе расположенные относительно системы координат.

5. Цилиндры второго порядка. Уравнения эллиптического (рис. 28), гиперболического (рис. 29) и параболического (рис. 30) цилиндров имеют вид соответственно.

Рис. 28 Рис. 29 Рис. 30

Поверхности, которые задаются уравнениями или 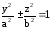, а также 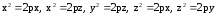, являются иначе располо-женными относительно системы координат цилиндрами.

Общие методы приведения уравнения поверхности второго порядка используют теорию квадратичных форм и здесь на рассматриваются. Рассмотрим только слу-чай, когда коэффициенты D, E и F ( при xy, yz, xz соответственно) равны нулю. В этом случае уравнения (28) с помощью параллельного переноса осей координат легко приводятся к каноническому виду.