ТЕМА 1

ЛИНЕЙНАЯ АЛГЕБРА

1. 1. Матрицы и определители

1.2. Система линейных уравнений

Задачи по теме «Линейная алгебра»

Задача 1. Вычислить определитель III-го порядка:

а) по правилу треугольников ,

б) по теореме разложения , используя свойства определителей .

Решение.

а)

б) прибавим вторую строку сначала к первой, а затем к третьей строкам. Полученный определитель разложим по элементам второго столбца , , :

Ответ:

Задача 2. Используя свойства определителей и теорему разложения , вычислить определитель IV порядка:

Решение.

Ответ:

Задача 3. Даны матрицы А и В. Найти матрицу где

Решение. Найдем слагаемые матрицы С, потом подставим их в правую часть равенства.

5

6

4

Ответ:

4

Задача 4. Решить данную систему линейных уравнений:

а) по формулам Крамера ;

30

б) матричным методом ;

31

в) методом Гаусса .

32

Решение.

а) Формулы Крамера:

.

30

Так как т.е. определитель системы отличен от нуля, система имеет единственное решение. Остается найти , подставив найденные и в любое из уравнений системы, например в первое:

Проверка: подставим найденные значения , , в каждое уравнение системы:

Ответ: , , .

б) Матричный метод:

Введем обозначения

- матрица, составленная из коэффициентов при неизвестных, матрица системы;

- матрица из неизвестных системы;

- матрица из свободных членов системы.

С помощью этих матриц данную систему уравнений можно записать так:

.

Решив это уравнение относительно матрицы (матрицы неизвестных) ,

31

,

найдем решение системы.

Составим матрицу , обратную по отношению к матрице, т.е. :

:

7

1. (см решения этой системы по формулам Крамера).

14

2. Составим матрицу (присоединенную), элементами которой являются алгебраические дополнения соответствующих элементов матрицы :

, где ,

а именно - произвольный элемент новой матрицы; - алгебраическое дополнение элемента матрицы ; - минор этого элемента.

3. Транспонируем полученную матрицу , имеем .

6

4. Запишем .

Остается найти матрицу :

,

т.е. , отсюда по получим Ответ:

в) Метод Гаусса (метод последовательного исключения неизвестных) .

Выполняя элементарные преобразования над строками данной матрицы, стараемся придать ей «форму трапеции», т.е. обращаем в нули элементы, расположенные под главной диагональю матрицы, исключая неизвестные:

~ ~

+

Полученная матрица равносильна исходной. Восстановим систему уравнений, соответствующую последней матрице (выполним «обратный ход»):

Ответ: , , .

Замечание 1. Если ранг матрицы системы и ранг ее расширенной матрицы равны, т.е. , то система совместна .

22

В нашем примере .

Если, кроме того, , где - число неизвестных, то система имеет единственное решение. В нашем примере .

26

32

Задача 5. Решить следующие системы линейных уравнений методом Гаусса: , , .

33

34

а)

Решение.

~ ~ .

Делаем «обратный ход»:

Последнее уравнение не имеет решений.

23

Ответ: система противоречива, т.е. не имеет решений .

Замечание 2. Проанализировав последнюю матрицу, можно заметить, что , а , т.е. решений у системы нет .

23

б)

Решение.

~ ~ .

Система уравнений, соответствующая этой матрице, имеет вид

Так как число уравнений меньше числа неизвестных, то система неопределенная, т.е. имеет бесконечно много решений . Допустим - любое действительное число, тогда

27

или а

Проверка: Допустим , тогда ,, подставим эти значения неизвестных в систему:

Ответ: или .

Замечание 3. В нашем примере легко увидеть по матрице, полученной в результате элементарных преобразований, что , но число неизвестных . Число свободных переменных (у нас это ). Так как - любое действительное число, у системы уравнений бесконечно много решений, определяемых по формулам, приведенным в ответе.

27

в)

Решение.

~ ~ .

Запишем систему уравнений, соответствующую последней матрице, отбросив «лишнюю» строку:

Так как число уравнений меньше числа неизвестных, то система неопределенная, т.е. имеет бесконечно много решений .

29

Пусть - любое действительное число – свободная переменная, выразим через нее и :

.

Проверка: положим , тогда , .

Ответ: или .

25

Замечание. Однородная система уравнений всегда совместна . В примере , а - число неизвестных; значит, система неопределенная, - число свободных переменных . У нас в примере это .

29

г)

Решение.

~

Запишем систему уравнений, соответствующую последней матрице, т.е. выполним «обратный ход»:

Ответ: .

25

Замечание. Так как однородная система линейных уравнений всегда совместна , а из последней матрицы, полученной из матрицы систем путем элементарных преобразований, видно, что , т.е. , то данная однородная система имеет единственное решение, т.е. нулевое решение.

28

Тема 2 векторная алгебра

Задачи по теме «Векторная алгебра»

Задача 1. Даны векторы и . Найти вектор .

Решение. Так как вектор - линейная комбинация векторов и , используем теорему о свойстве линейных операций над векторами , т.е. сведем данные в задаче линейные операции над векторами к таким же операциям над их координатами:

3

5

;

;

.

Ответ: .

Задача 2. Даны векторы , , . Выяснить, можно ли принять векторы и за базисные, и если можно, то выразить вектор через них. Найти координаты вектора 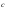относительно базиса и .

Решение.

а) Вначале проверим коллинеарность векторов и , составив и сравнив отношения их одноименных координат . Из этого неравенства следует, что векторы и неколлинеарны, значит, линейно независимы, т.е. могут быть приняты за базис .

4

5

б) В базисе и выразим вектор , как их линейную комбинацию: , где и - неизвестные пока коэффициенты . Используя теорему о свойстве линейных операций над векторами , перейдем в полученном равенстве к координатам:

4

5

Решив эту систему, получим , , подставим их в линейную комбинацию: - это разложение вектора в базисе и , а коэффициенты справа – координаты вектора в базисе и .

Ответ: , или .

Задача 3. Доказать, что точки , , и служат вершинами трапеции. Выяснить, которое из оснований трапеции длиннее другого, во сколько раз.

Решение. Найдем координаты векторов, последовательно соединяющих данные точки . , ; , . Легко увидеть, что векторы и удовлетворяют условию коллинеарности : , . Следовательно, , значит, , т.е. , а . Проверим коллинеарность векторов и : . Значит четырехугольник - трапеция.

5

5

Задача 4. Найти орт и направляющие конусы вектора , если , .

Решение. Найдем координаты вектора : . Его длина по формуле : . Так как орт вектора определяют по формуле , , по

5

7

7

6

.

Ответ: ; .

Задача 5. На материальную точку действуют силы ; ;. Найти работу равнодействующей этих сил при перемещении точки из положения в положение .

Решение. Работа силы на пути вычисляется по формуле : (механический смысл скалярного произведения). Найдем вектор , т.е. , а вектор пути . По формуле скалярного произведения векторов в ДСК получим .

6

5

7

Ответ: .

Задача 6. Даны векторы и . Найти проекцию вектора на направление вектора .

Решение. Чтобы воспользоваться формулой проекции вектора на вектор : , найдем координаты вектора , длину вектора и скалярное произведение

6

5

7

. Теперь подставим в формулу найденные значения .

7

Ответ: .

Задача 7. Найти острый угол между диагоналями параллелограмма, построенного на векторах 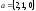и .

Решение. Найдем, например, косинус угла , который образует векторы и , координаты которых находим по формулам и : ; .

Далее используем формулу :

, где

;

, .

Замечание: т.к. оказался положительным, то - острый угол; косинус угла, смежного с углом , отличается от знаком.

Задача 8. Даны вершины четырехугольника , , и . Доказать, что его диагонали взаимно перпендикулярны.

Решение. Если два вектора взаимно перпендикулярны, то их скалярное произведение равно нулю . Найдем векторы, совпадающие с диагоналями четырехугольника : , . Вычислим скалярное произведение этих векторов : . Диагонали прямоугольника взаимно перпендикулярны

6

5

7

.

7

Задача 9. Векторы и образуют угол . Зная, что , , найти длину вектора .

Решение. Используем формулу :

6

,

т.к. , , .

Ответ: .

Задача 10. Найти площадь треугольника с вершинами в точках , , .

Решение. Рассмотрим векторы и , совпадающие со сторонами данного треугольника : и . Используя геометрический смысл векторного произведения двух векторов : , вычислим сначала векторное произведение : - это вектор. Теперь найдем его модуль : .

.

Ответ: кв.ед.

Задача 11. Найти площадь параллелограмма, построенного на векторах и , где , , а угол между векторами и равен .

Решение. По формулам :

кв. ед.

В решении задачи использован распределительный закон, которому подчиняется векторное произведение векторов и свойства векторного произведения: и , а также формула .

Ответ: кв. ед.

Задача 12. Вычислить объем пирамиды, вершины которой находятся в точках , , .

Решение. Найдем координаты векторов, совпадающих с ребрами пирамиды, прилежащими к одной из вершин ее, например , , . Используя геометрический смысл смешанного произведения

, найдем объем параллелепипеда, а затем – объем пирамиды, который равен объема параллелепипеда. По формуле :

куб. ед.

Ответ: куб ед.

Задача 13. Доказать, что четыре данные точки , , лежат в одной плоскости.

Решение. Чтобы решить задачу, достаточно доказать, что три вектора, соединяющие данные точки, компланарны, т.е. лежат в одной плоскости. Смешанное произведение компланарных векторов равно нулю . Введем в рассмотрение векторы , , и вычислим их смешанное произведение:

10

,

что и требовалось доказать.

ТЕМА 3

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

3.1 Прямая на плоскости

Задачи по теме «Прямая на плоскости»

Задача 1. Через точку провести прямые, параллельные осям координат.

Решение.

а) Если , то по уравнение : , а так как , то (координаты должны удовлетворять уравнению ).

1

б) Если , то по уравнение : , а так как , то (координаты должны удовлетворять уравнению ).

1

Ответ: :; : .

Задача 2. На каком расстоянии от начала координат проходит прямая ?

Решение. Воспользуемся формулой . Чтобы найти расстояние от точки - начала координат – до данной прямой , подставим в левую часть этого уравнения, вместо текущих координат, координаты точки , возьмем полученное число по модулю и поделим его на длину нормального вектора , т.е. на , имеем .

2

Ответ: .

Задача 3. Найти площадь треугольника, образованного прямой и осями координат. Построить эту прямую.

Решение. Приведем уравнение данной прямой к виду «в отрезках на осях» :

, т.е. к виду , где ,

- отрезки, отсекаемые прямой на осях координат.

Треугольник, образованный данной прямой и осями

координат, - прямоугольный, а катеты его равны 3 и 7. Тогда:

кв. ед.

Ответ: кв.ед.

Задача 4. Даны точка и вектор . Через точку провести две прямых, одна из которых параллельна, а другая перпендикулярна вектору .

Решение.

а) - воспользуемся уравнением , где и - координаты точки, лежащей на прямой, а - направляющий вектор прямой. Приняв за него вектор , получим: или .

б) – воспользуемся уравнением , где точка принадлежит прямой, а вектор – нормаль к прямой, за которую примем вектор : или .

Ответ: : ; : .

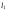Задача 5. Какие углы с осью образуют прямые, проходящие через точки:

а) и ; б) и ; в) и ?

Решение. Используем уравнение прямой, проходящей через две данные точки :

.

а) или , где , т.е. , .

б) или , где , т.е. , .

в) или , где не существует, т.е. , .

Ответ: ; ; .

Задача 6. Найти углы, которые получатся при пересечении двух данных прямых и .

Решение. Воспользуемся формулой : , и - где угловые коэффициенты данных прямых соответственно. Преобразуем уравнение данных прямых к виду : ; . Тогда т.е. угол, который образует первая прямая со второй, ; второй, смежный с ним, который образует вторая прямая с первой, .

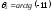Ответ: .

Задача 7. Через точку пересечения прямых и провести две прямые, одна из которых параллельна, а другая перпендикулярна прямой ( , ).

Решение. Воспользуемся уравнением , где - угловой коэффициент прямой, а - точка, через которую проходит искомая прямая. Вначале найдем точку, как точку пересечения данных прямых, решив совместно их уравнения:

4

а) первая из искомых прямых параллельна прямой , следовательно, ее угловой коэффициент , т.к. уравнение можно записать так: . Подставив в уравнение , найденные параметры получим: или .

9

4

б) вторая из искомых прямых перпендикулярна , следовательно, ее угловой коэффициент . Тогда уравнение второй - искомой прямой: или .

10

Ответ: ; .

Задача 8. Показать, что точки , и лежат на одной прямой.

Решение. Через точки и проведем прямую : , или , или . Чтобы убедиться, что точка тоже лежит на этой прямой, подставим координаты этой точки в полученное уравнение прямой . Задача решена.

8

Задача 9. Даны координаты вершин треугольника: , ,. Найти уравнение медианы , проведенной из вершины к стороне , и вычислить ее длину.

Решение. а) Найдем координаты точки - середины отрезка по формулам:

, ; .

Уравнение медианы составим, используя уравнение прямой, проходящей через две данные точки и : , или .

б) Длину медианы вычислим по формуле:

.

Ответ: а) ; б) .

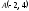Задача 10. Найти точку , симметричную точке относительно прямой .

Решение. Искомая точка симметрична точке относительно прямой , если она лежит на одном с ней перпендикуляре к прямой : , и на одинаковом расстоянии от прямой : .

а) Составим уравнение прямой : , где , т.к. и ; или .

б) Найдем точку – точку пересечения прямых и , решив систему их уравнений:

- проверьте!

в) Так как - середина отрезка . Воспользуемся формулами деления отрезка пополам, приведенными в предыдущей задаче. Подставив в них известные величины и , получим уравнения , . Отсюда , .

Ответ: .