Тема №3. Расчет ферм. Трение скольжения и качения.

В данной лекции рассматриваются следующие вопросы

1. Равновесие системы тел.

2. Расчет ферм.

3. Понятие о ферме.

4. Аналитический расчет плоских ферм.

5. Графический расчет плоских ферм.

6. Трение.

7. Законы трения скольжения.

8. Реакции шероховатых связей.

9. Угол трения.

10. Равновесие при наличии трения.

11. Трение качения и верчения.

12. Момент силы относительно центра как вектор.

13. Момент пары сил как вектор.

14. Момент силы относительно оси.

15. Зависимость между моментами силы относительно центра и относительно оси.

16. Приведение пространственной системы сил к данному центру.

17. Условия равновесия произвольной пространственной системы сил.

18. Задачи на равновесие тела под действием пространственной системы сил.

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

Равновесие систем тел.

Статический расчет инженерных со­оружений во многих случаях сводится к рассмотрению условий равновесия конструкции из системы тел, соединенных какими - нибудь связями. Связи, соединяющие части данной конструкции, будем называть внутренними, в отличие от внешних связей, скрепляющих конструк­цию с телами, в нее не входящими (например, с опорами).

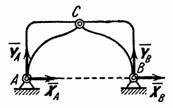
Рис.22

Если после отбрасывания внешних связей (опор) конструкция остается жесткой, то для нее задачи статики решаются как для аб­солютно твердого тела.

Однако могут встречаться такие инженерные конструкции, которые после отбрасывания внешних связей не остаются жесткими. Примером такой конструкции является трехшарнирная арка (рис. 22). Если отбросить опоры А и В, то арка не будет жесткой: ее части могут поворачиваться вокруг шар­нира С.

На основании принципа отвердевания система сил, действующих на такую кон­струкцию, должна при равновесии удов­летворять условиям равновесия твердого тела. Но эти условия, как указывалось, будучи необходимыми, не будут являться достаточными, поэтому из них нельзя будет определить всех неизвестных. Для решения задачи необходимо будет дополнительно рассмотреть равновесие какой-ни­будь одной или нескольких частей конструкции.

Например, составляя условия равновесия для сил, действующих на трех шарнирную арку (см. рис. 22), мы получим три уравнения с четырьмя неизвестными ,,,. Рассмотрев дополнительно условия равновесия левой (или правой) ее половины, мы получим еще три уравнения, содержащие два новых неизвестных,, на рис. 22 не показанных. Решая полученную систему шести уравнений, найдем все шесть неизвестных.

Другой способ решения подобных задач состоит в том, что кон­струкцию сразу расчленяют на отдельные тела и составляют усло­вия равновесия каждого из тел, рассматривая его как свободное. При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструк­ции из n тел, на каждое из которых действует произвольная плоская си­стема сил, получится таким путем 3n уравнений, позволяющих найти 3n неизвестных (при других системах сил число уравнений соответственно изменится). Если для данной конструк­ции число всех реакций связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.