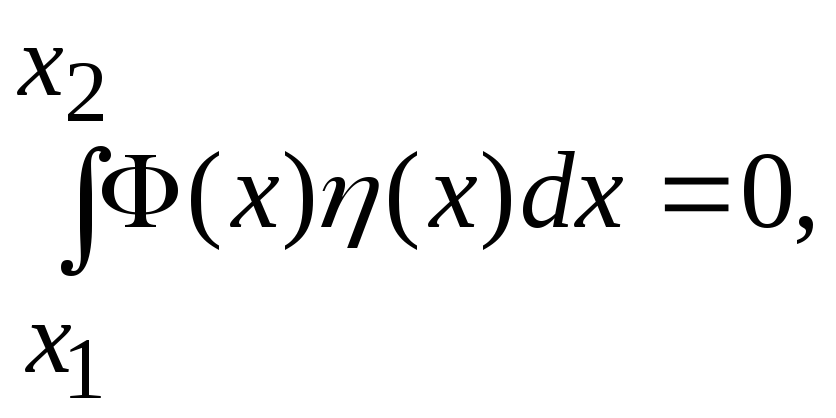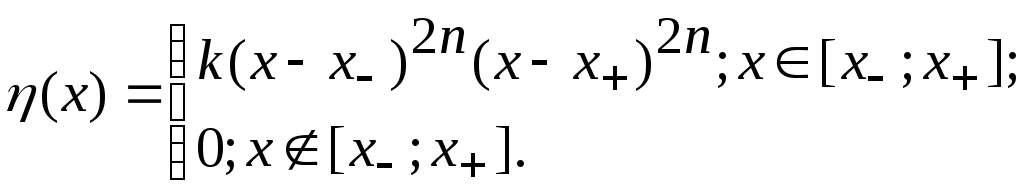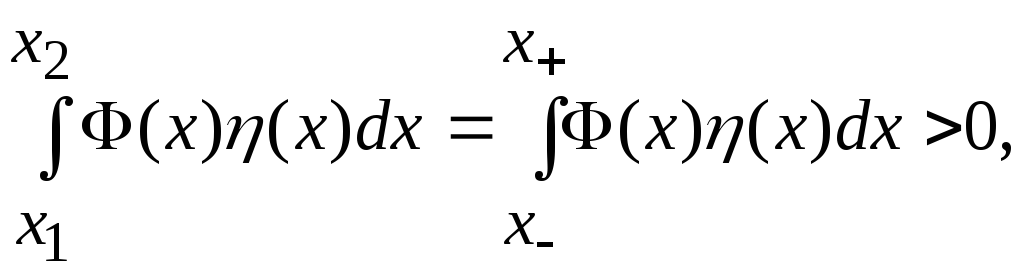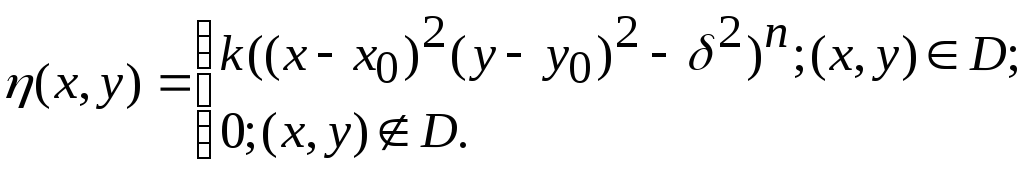- •Оптимизация в автоматизированных системах управления
- •Предисловие
- •1. Критерии оптимальности автоматизированных систем управления
- •Контрольные вопросы
- •2. Основные понятия и определения вариационного исчисления
- •2.1. Введение в вариационное исчисление
- •2.2. Выполнение заданий
- •Контрольные вопросы
- •3. Основная лемма вариационного исчисления
- •1. Лемма Лагранжа
- •3.2. Выполнение заданий
- •Контрольные вопросы
- •4. Решение вариационных задач с использованием дифференциального уравнения эйлера
- •4.1. Дифференциальное уравнение Эйлера
- •4.2. Выполнение заданий
- •Контрольные вопросы
- •5. Исследование экстремалей функционалов
- •5.1. Выполнение заданий
- •Задание 2
- •6.2. Выполнение заданий
- •Задание 2
- •7.2. Выполнение заданий
- •Задание 1
- •Контрольные вопросы
- •Библиографический список
- •Приложение элементы программирования на matlab
- •1. Символические вычисления
- •2. Построение графиков
- •3. Решение конечных уравнений
- •4. Решение дифференциальных уравнений
- •Содержание
Контрольные вопросы
В чём состоит основная задача вариационного исчисления?
Какое утверждение правильное: C0
 C1
или C1
C1
или C1 C0?
C0?
Если на функции y(x) достигается сильный экстремум, то достигается ли слабый? А если достигается слабый, то достигается ли сильный?
3. Основная лемма вариационного исчисления
1. Лемма Лагранжа
Важную роль в вариационном исчислении играет лемма Лагранжа, которая называется основной леммой вариационного исчисления. Она используется при выводе дифференциальных уравнений Эйлера. Сформулируем и докажем эту лемму для функции одной переменной.
Лемма.
Если ![]() η(x)
η(x)![]() Ck
на [x1,
x2]
интеграл от произведения этой функции
на другую функцию Φ(x)
Ck
на [x1,
x2]
интеграл от произведения этой функции
на другую функцию Φ(x)
![]() Ck
по [x1,
x2]
равен нулю:
Ck
по [x1,
x2]
равен нулю:
|
|
(1) |
то
это возможно только в том случае, если
Φ(x)≡0
![]() x
x![]() [x1,
x2].
[x1,
x2].
Доказательство.
Проведём доказательство от противного.
Пусть в какой-либо точке x0![]() [x1,
x2]:
Φ(x0)≠0.
Для определённости будем считать, что
Φ(x0)=A>0.
Свойством функции, непрерывной на
интервале, является то, что если
непрерывная функция в какой-то точке
x0
отлична от нуля, то существует некоторая
малая окрестность этой точки, в которой
функция тоже отлична от нуля и имеет
тот же знак, что и в точке x0.
В нашем случае Φ(x)
[x1,
x2]:
Φ(x0)≠0.
Для определённости будем считать, что
Φ(x0)=A>0.
Свойством функции, непрерывной на
интервале, является то, что если
непрерывная функция в какой-то точке
x0
отлична от нуля, то существует некоторая
малая окрестность этой точки, в которой
функция тоже отлична от нуля и имеет
тот же знак, что и в точке x0.
В нашем случае Φ(x)
![]() Ck,
то есть является непрерывной. Поэтому
существует некоторый интервал [x−, x+],
в котором Φ(x)>0.
Ck,
то есть является непрерывной. Поэтому
существует некоторый интервал [x−, x+],
в котором Φ(x)>0.
Покажем
теперь, как можно построить такую функцию
η(x)
![]() Ck,
что (1) будет нарушаться. Возьмём η(x)
в виде
Ck,
что (1) будет нарушаться. Возьмём η(x)
в виде
|
|
(2) |
За счёт показателя n можно добиться дифференцируемости нужное число раз, а за счёт k − сделать функцию сколь угодно большой или малой.
Тогда (1) будет нарушаться:
|
|
(3) |
Так
как каждый из сомножителей под интегралом
положительный. Аналогично, если в
какой-либо точке Φ(x0)<0,
то для этой же η(x)
интеграл (3) будет отрицательный. Отсюда
по принципу от противного следует, что,
если ![]() η(x)
будет выполняться (1), то это возможно,
только если Φ(x)≡0.
η(x)
будет выполняться (1), то это возможно,
только если Φ(x)≡0.
Замечание.
Основная лемма вариационного исчисления
справедлива и для функции нескольких
переменных. Сформулируем и докажем её
для функции двух переменных. Формулируется
она так: если ![]() η(x,y)
η(x,y)
![]() Ck
в области D
Ck
в области D
|
|
(4) |
то
это возможно только в том случае, если
Φ(x,y)≡0
![]() (x,y)
(x,y)
![]() D.
D.
Доказательство
проводится так же, методом от противного.
Предположим, что в какой-то точке (x0,y0)
![]() D:
Φ(x0,y0)=A>0.
Значит, существует некоторая малая
δ‑окрестность точки (x0,y0),
в которой Φ(x0,y0)>0.
Построим функцию η(x,y)
в виде
D:
Φ(x0,y0)=A>0.
Значит, существует некоторая малая
δ‑окрестность точки (x0,y0),
в которой Φ(x0,y0)>0.
Построим функцию η(x,y)
в виде
|
|
(5) |
Для этой функции η(x,y) условие (4) будет нарушаться: подынтегральная функция будет отлична от нуля (причём положительна) только в δ -окрестности точки (x0,y0), поэтому интеграл (4) будет положительный. Аналогично, если в какой-то точке Φ(x0,y0) < 0, то для подобранной нами η(x,y) интеграл (4) будет отрицательный. Следовательно, добиться выполнения (4) при произвольной η(x,y) можно, только если Φ(x,y) ≡ 0.
3.2. Выполнение заданий
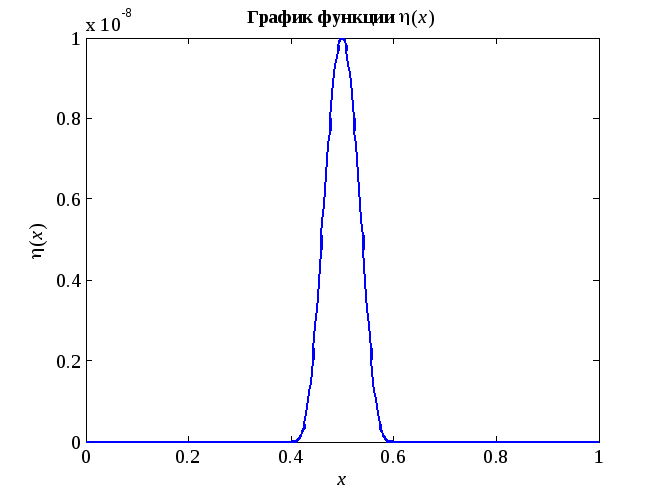
Задание
1. Нарисуйте
с помощью MATLAB пример функции η(x)
![]() Ck
в соответствии с (2) для n
= 2 и k
=1 при x−=0,4
и x+=0,6.
Ck
в соответствии с (2) для n
= 2 и k
=1 при x−=0,4
и x+=0,6.
clear all % очистили всё
Xminus=0.4;
Xplus=0.6;
n=2;
k=1;
x=linspace(Xminus,Xplus);
y=k.*(x-Xminus).^(2*n).*(x-Xplus).^(2*n);
plot([0 x 1],[0 y 0]) % рисуем
set(get(gcf,'CurrentAxes'),...
'FontName','Times New Roman Cyr','FontSize',12)
title('\bfГрафик функции \rm\eta\rm(\itx\rm)')
xlabel('\itx') % метка оси OX
ylabel('\eta\rm(\itx\rm)') % метка оси OY
xlim([0 1]); % пределы по оси OX.
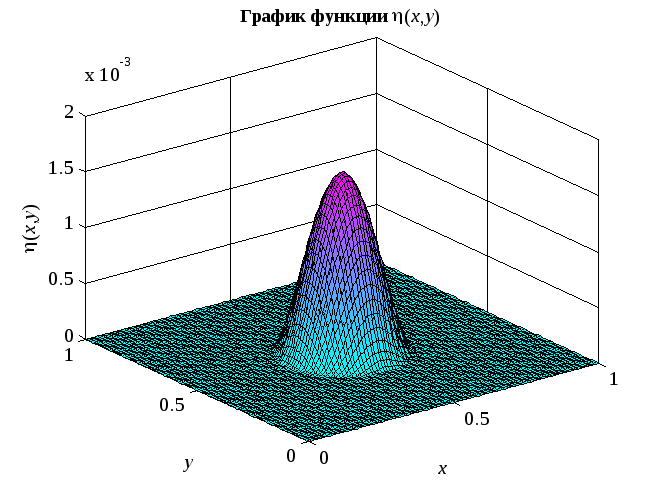
Задание 2. Нарисуйте трёхмерный график этой функции с помощью MATLAB для n =2 и k =1 при x0=0,5, y0=0,5, δ=0,2.
Чтобы вычислить функцию z на заданной сетке, надо провести вычисления по первой части формулы (5), а затем умножить поэлементно на булевский массив. При этом происходит автоматическое приведение типов, и булевский массив преобразуется в массив нулей и единиц. Таким образом, в области D вычисления проводятся по первой части (10), а вне D будет 0.
clear all % очистили всё
x0=0.5;
y0=0.5;
delta=0.2;
n=2;
k=1;
[X,Y]=meshgrid(linspace(0,1),linspace(0,1));
z=k.*((X-x0).^2+(Y-y0).^2-delta^2).^n.*...
((delta^2-(X-x0).^2-(Y-y0).^2)>0);
surf(X,Y,z) % рисуем
set(get(gcf,'CurrentAxes'),...
'FontName','Times New Roman Cyr','FontSize',12)
title(['\bfГрафик функции '...
'\rm\eta\rm(\itx\rm,\ity\rm)']) % заголовок
xlabel('\itx') % метка оси OX
ylabel('\ity') % метка оси OY
zlabel('\eta\rm(\itx\rm,\ity\rm)') % метка оси OZ