5. Принцип наложения при расчёте электрических цепей

Принцип наложения:ток в любой ветви электрической цепи равен алгебраической сумме токов, вызываемых каждым источником электрической энергии в отдельности. Этот принцип справедлив для всех линейных электрических цепей.

Принцип наложения применяется в методе расчета, получившем название метода наложения. При использовании данного метода поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждого источника электрической энергии в отдельности, мысленно удаляя остальные источники из схемы. При этом внутренние сопротивления источников должны остаться в цепи. Это означает, что участок ветви, в котором был источник ЭДС, замыкается накоротко (рис. 4.16а), а участок с источником тока размыкается (рис. 4.16б). Затем находят фактические токи в ветвях путем алгебраического сложения частичных токов. Если направление частичного тока совпадает с выбранным направлением фактического тока, то при суммировании частичный ток берется со знаком “ + ”, иначе “ - ”.

6. Амплитуда, частота, начальная фаза синусоидально изменяющегося тока, напряжения, эдс

Обозначения мгновенных значений синусоидальных ЭДС, напряжения и тока являются однотипными:

, (2.1)

, (2.2)

, (2.3)

где -амплитудатока (рис. 2.1);-угловая частота. Размерность.

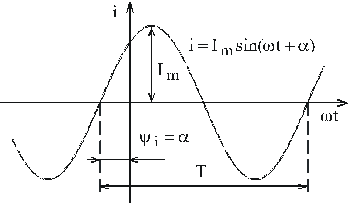
Рис. 2.1

Аргумент, стоящий под знаком синуса , называетсяфазой. Она характеризует состояние колебания (то есть его численное значение) в любой момент времени.

Значение фазы в момент времени t= 0

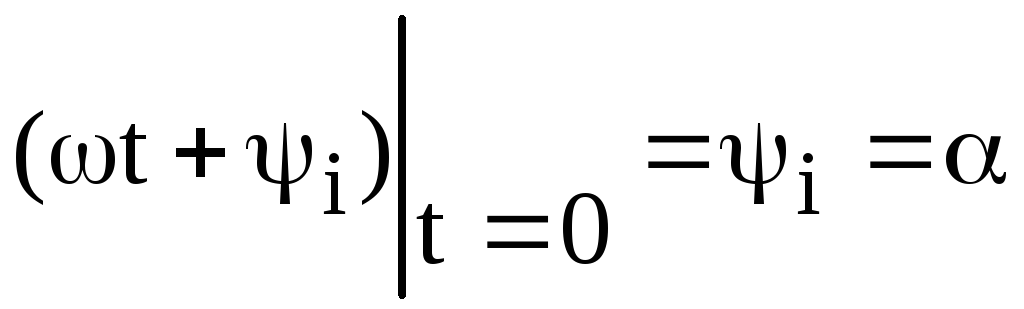
называется начальной фазой. Она характеризует состояние колебания (то есть его численное значение) приt= 0. Для обозначения начальных фаз напряжения и тока часто используют буквыи.

Частотатокаfпоказывает, сколько полных колебаний происходит за одну секунду. Величиныfисвязаны соотношением

,

где f– частота, Гц.

7. Действующие и средние значения синусоидально изменяющихся токов, напряжений ,эдс

Средним значением за периодТ любой периодической функцииназывается величина

. (2.5)

В случае синусоидальной функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площадью отрицательной. В этом случае пользуются средним значением за полупериод:

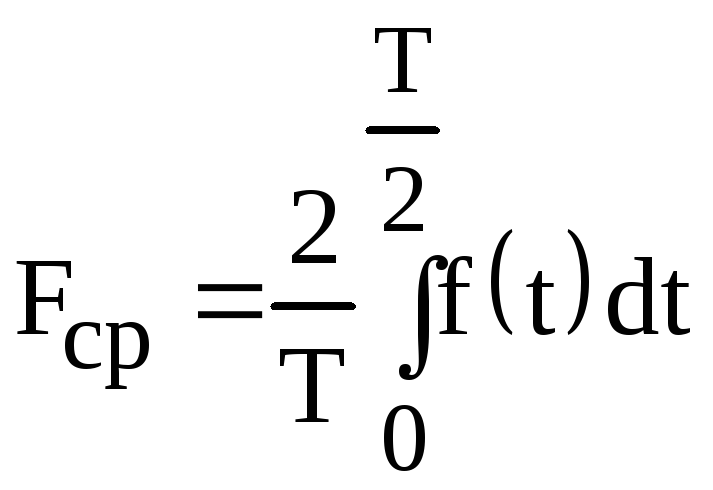. (2.6)

Среднее значение за полупериод показывают электроизмерительные приборы выпрямительной системы.

Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым течет один и тот же ток, пропорциональны квадрату тока. Поэтому о величине переменного тока судят по так называемому действующему (среднеквадратичному) значениюза период

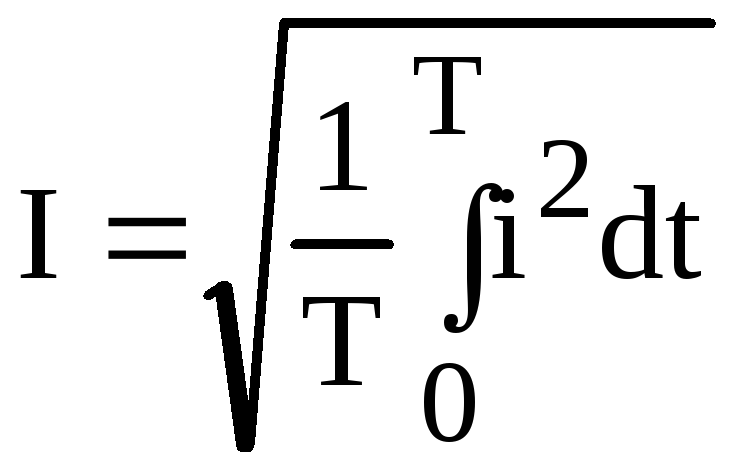. (2.9)

8. Мгновенная, активная, реактивная и полная мощности

Мгновенная мощность, поступающая в двухполюсник:

. (2.60)

График мгновенной мощности приведен на рис. 2.18. На интервале I, когда напряжениеuи токiимеют разные знаки, энергия возвращается из двухполюсника в источник ЭДС. На интервалеII, когда напряжение и ток имеют одинаковые знаки, энергия направлена из источника в двухполюсник. Процесс обмена энергией между источником и приемником обусловлен наличием реактивных элементов в пассивном двухполюснике.

Активная мощность, рассеиваемая в двухполюснике:

. (2.61)

Раскрывая (2.61), получим

. (2.62)

Множитель называетсякоэффициентом мощности. Как было показано выше, активная мощность может быть только положительной. Следовательно, коэффициент мощности также всегда больше нуля и

. (2.63)

Величина

(2.64)

называется полной мощностью. Она соответствует той максимальной активной мощности, которая может быть получена в цепи при заданных действующих значениях напряженияUи токаI. Размерность полной мощности [S] = ВА.

Любая электрическая установка (например, трансформатор, двигатель) проектируетcя и изготавливается на полную мощностьS. Однако из-за наличия угла сдвига фазмежду напряжением и током расчетная мощность установкиSиспользуется не полностью. Отсюда ясна важность высокого значения коэффициента мощности.

Величина

(2.65)

называется реактивной мощностью. Реактивная мощность характеризует скорость передачи электрической энергии от источника энергии к приемнику и обратно.

Реактивная мощность положительна при отстающем токе и отрицательна при опережающем токе.

Размерность реактивной мощности [Q] = ВАp.