7.5. Дана плотность распределения непрерывной случайной величины X:

Найти коэффициент A . Определить математическое ожидание и среднее квадратическое отклонение.

7.6. Случайная величина X распределена по "Закону прямоугольного треугольника" в интервале (0, а).

f(x)

x

^{0 а}

Написать выражение плотности распределения. Найти функцию распределения. Найти вероятность попадания случайной величины X на участок от а/2 до а. Найти характеристики случайной величины Х: .

7.7. Известна функция распределения срока службы блока

Найти коэффициент K .Найти средний срок службы и дисперсию срока службы блока.

7.8. Плотность вероятности случайной величины Х задана функцией:

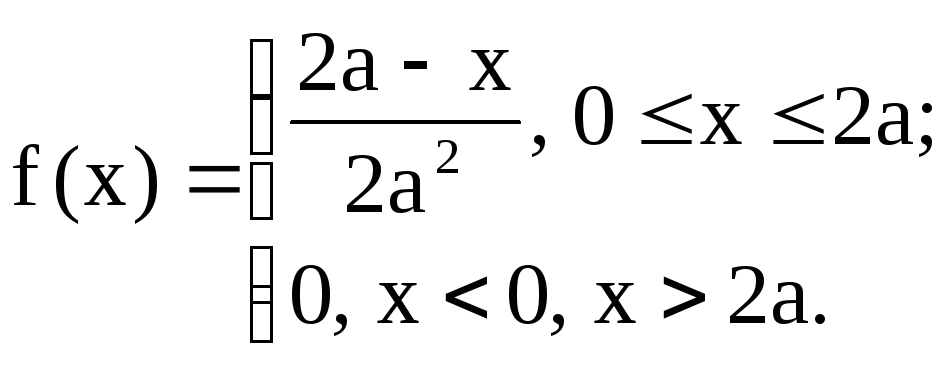
Найти ее функцию распределения, построить графики плотности вероятности и функции распределения.

7.9. Плотность распределения времени безотказной работы электронно-лучевой трубки имеет вид (по закону Вейбулла)

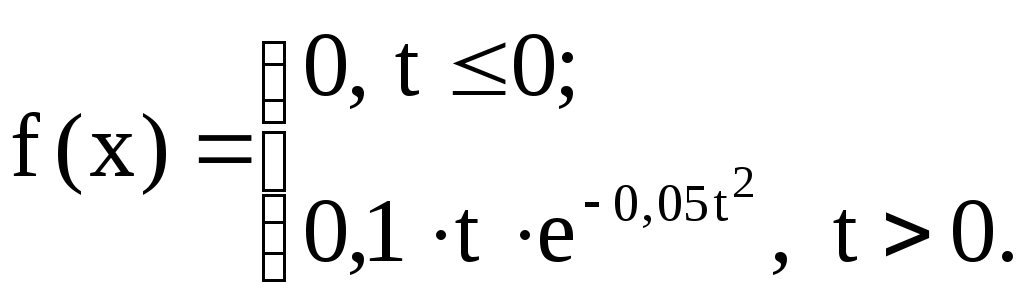
Найти функцию распределения случайной величины T и вероятность безотказной работы трубки в течение 4 часов.

7.10. Случайная величина X подчинена закону Симпсона ("Закону равнобедренного треугольника") на участке от -a до a .

f(x)

x

-a 0 a

Написать выражение плотности распределения. Найти функцию распределения. Найти числовые характеристики случайной величины X: Найти вероятность попадания случайной величины X в интервал (-a/2; a ).

7.11. Плотность распределения непрерывной случайной величины в интервале равна, вне этого интервалаf(x) =0. Найти вероятность того, что в трех независимых испытаниях случайная величина X примет ровно два раза значение, заключенное в интервале (0;) .

7.12. Дана плотность распределения вероятностей непрерывной случайной величины

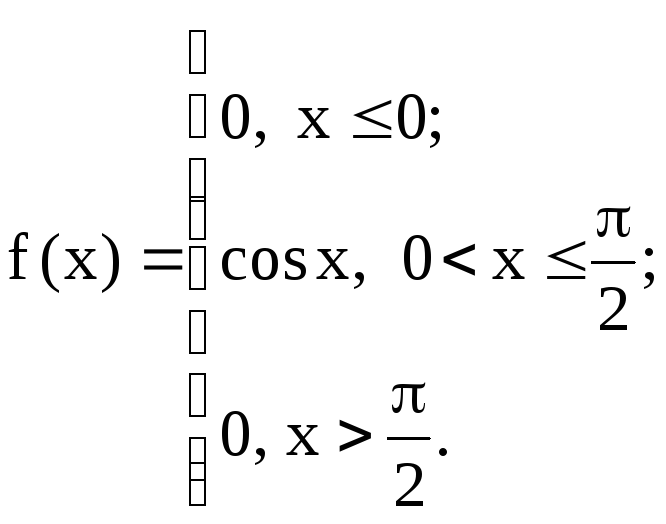
Найти функцию распределения. Построить графики функций f(x) и F(X) .

7.13. Найти математическое ожидание и дисперсию случайной величины X, распределенной в интервале () с плотностью вероятностей, вне этого интервала f(x) = 0.

7.14. Дана плотность вероятности случайной величины X: Построить графики функций f(x) и F(x). Найти вероятность попадания случайной величины X в интервал ( -1; 1) и показать ее на графиках.

7.15. Непрерывная случайная величина X задана законом распределения

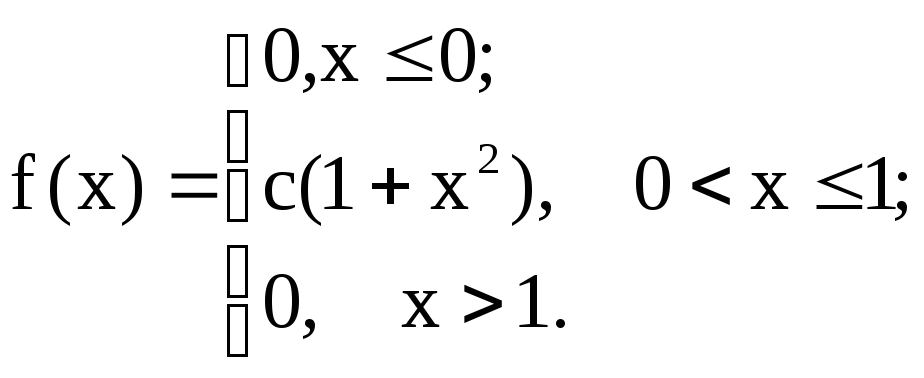
Найти: 1) коэффициент C; 2) функцию распределения F(x); 3) математическое

ожидание и дисперсию X.

7.16. Случайная величина X задана плотностью распределения:

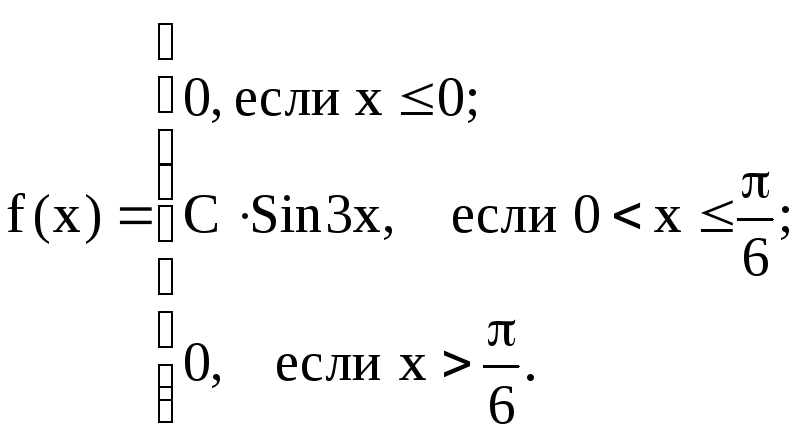
Найти:1) коэффициент C; 2) функцию распределения F(x); 3) вероятность попадания случайной величины на интервал (/6;/4); 4) математическое ожидание X.

7.17. Непрерывная случайная величина подчинена закону распределения с плотностью

Найти коэффициент c, М[X], D[X]. Построить график функции распределения F(x).

7.18. Плотность распределения случайной величины Х задана графически :

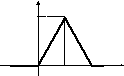f(х) Написать выражение плотности распре-

деления f(х); найти функцию распре-

деления и построить ее график; найти

математическое ожидание и дисперсию.

_{0 2 4} x

7.19. Случайная величина X распределена логарифмически нормально, т. е. ее плотность

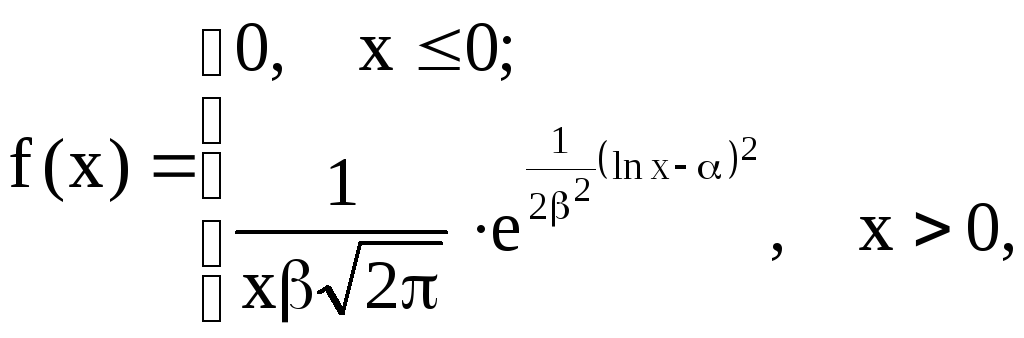
где а - любое действительное число, - положительно. Найти M[X].

7.20. Плотность распределения вероятности случайной величины . Требуется: а) найти коэффициент a ,б) найти функцию распределения случайной величины X , в) вычислить вероятность попадания случайной величины в интервал (0; 1/k).

7.21. Плотность распределения вероятности случайных амплитуд боковой качки корабля имеет вид (закон Рэлея) 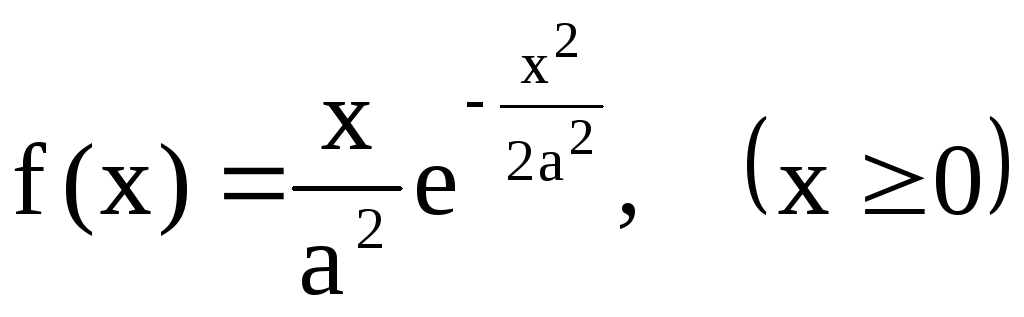.Определить: а) функцию распределения случайной величины X; б) математическое ожидание M[X], дисперсию D[X] , среднее квадратическое отклонение_x.

7.22. Функция f(x) равна нулю при - < x < 1 и равна , если 1x < +. Найти: а) значение A , при котором эта функция будет плотностью вероятности некоторой случайной величины X; б) функцию распределения этой случайной величины; в) вероятность того, что в четырех независимых испытаниях она ни разу не попадает в интервал (1; 2).

7.23. Функция является плотность распределения вероятности случайной величины Х. Определить: а) коэффициент А; б) функцию распределения F(x), в) вероятность того, что случайная величина Х примет значение, не меньше единицы.

7.24. Случайная величина X может принимать только неотрицательные значения, ее функция распределения . Найти: а) плотность распределения вероятности; б) математическое ожидание M[X]. Построить графикиf(x) и F(x).