Х 1 3 5 7 9 р 0,1 0,2 0,3 0,3 0,1

Найти распределение случайной величины

6.24. В шестиламповом радиоприемнике (все лампы различные) перегорела одна лампа. С целью устранения неисправности наудачу выбранную лампу заменяют заведомо годной из запасного комплекта, после чего сразу проверяется работа приемника. Составить закон распределения числа замен ламп.

6.25. Имеется 5 ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании замка, если испробованный ключ в последующих попытках: а) не участвует; б) участвует.

6.26. В лотерее разыгрывается мотоцикл стоимостью 250 р., велосипед стоимостью 50 р. и часы за 40 р. Найти математическое ожидание выигрыша для лица, имеющего: а) 1 билет; б) 2 билета, если общее число билетов равно 100.

6.27. Из ящика, содержащего 2 белых и 4 черных шара, вынимают 3 шара и перекладывают в другой ящик, где имелось 5 белых шаров. Найти математическое ожидание числа белых шаров Х₁ и Х₂ в обоих ящиках.

6.28. В урне 4 белых и 5 черных шаров. Из урны наудачу один за другим без возвращения извлекают шары до тех пор, пока не появится черный шар. Найти закон распределения, математическое ожидание и дисперсию числа появившихся при извлечении белых шаров. Построить функцию распределения. Определить вероятность того, что число белых шаров будет не менее трех.

6.29. В партии из 7 деталей имеется 5 деталей первого сорта. Наудачу отобраны 3 детали. Найти закон распределения, математическое ожидание и дисперсию числа деталей первого сорта среди отобранных. Определить вероятность того, что число деталей первого сорта будет не менее двух.

6.30. Вероятность попадания в цель из орудия при первом выстреле равна 0,1, при втором выстреле равна 0,4, при третьем - 0,7. Предполагается произвести три выстрела. Найти закон распределения, математическое ожидание и дисперсию числа попаданий в цель. Построить функцию распределения. Определить вероятность того, что число попаданий не менее трех.

Задача № 7.

7.1. Дана функция распределения случайной величины X:

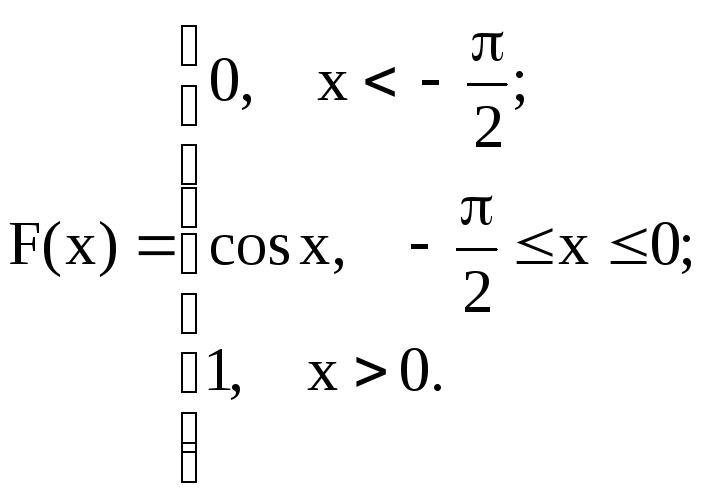
Найти вероятность попадания случайной величины X в интервал и показать эту вероятность на графиках плотности и функции распределения. Найти математическое ожидание и дисперсию.

7.2. График плотности распределения непрерывной случайной величины X имеет вид

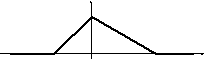f(x)

Найти функции f(x) и F(х).

Вычислить М[Х].

x

^{-2 0 4}

7.3. График плотности распределения непрерывной случайной величины X имеет вид

f(x) Найти математическое ожидание,

дисперсию и среднее квадрати-

ческое отклонение.

^{0 2} x

7.4.Случайная величина X задана плотностью распределения 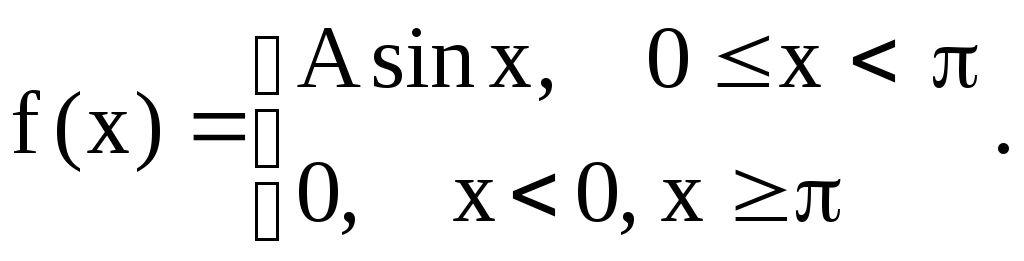Найти коэффициент A . Определить математическое ожидание и дисперсию случайной величины X. Найти функцию распределения и вероятность того, что значения случайной величины будут находиться в интервале (0;).