3.2.2. Примесная проводимость n - типа (γn)

Она возникает в полупроводнике, если в него ввести примесь, валентность которой больше, чем валентность полупроводника. Например, для четырехвалентного кремния – Si донорной примесью является пятивалентный мышьяк – As. Доноры располагаются в запрещенной зоне ближе к зоне проводимости. Для того, чтобы атом донора отдал свой электрон в зону проводимости, требуется очень малая энергия – Wпр Д (рис. 3.2, б). Например, ширина запрещенной зоны кремния – 1,12 эВ, а энергия активации донорной примеси (As) равна всего – 0,025 эВ. Атом мышьяка, отдавший свой электрон в зону проводимости, превращается в положительно заряженный ион, который хотя и имеет заряд, но закреплен в кристаллической решетке и в электропроводности не участвует.

Перенос зарядов происходит только за счет электронов

γ_n = q∙n∙u_n. (3.4)

Поэтому характер проводимости электронный; n - типа.

3.2.3. Примесная проводимость р – типа (γр)

Она возникает в полупроводнике, если в него ввести примесь, валентность которой меньше валентности основного полупроводника. Например, если в кремний ввести трехвалентный алюминий (Al), он является акцепторной примесью для Si. Акцепторы располагаются в запрещенной зоне ближе к зоне валентной. Их энергия активации также значительно меньше запрещенной зоны кремния (рис. 3.2, в), Wпр А ≈ 0,027 эВ. При такой энергии, полученной извне, акцептор захватывает электрон из валентной зоны, превращаясь при этом в отрицательно заряженный ион, а в валентной зоне начинается эстафетное перемещение электронов, т.е. будет иметь место дырочная проводимость

γ_р = q∙n∙u_р. (3.5)

Донор – дающий, акцептор – принимающий

3.2.4. Воздействие теплового поля на электропроводность

С увеличением температуры электропроводность полупроводников увеличивается экспоненциально. Такой характер поведения обусловлен носителями заряда. В общем случае подвижность носителей с увеличением температуры сначала изменяется пропорционально температуре в степени +3/2 (Т^+3/2), т.е. возрастает. Это происходит за счет небольшого увеличения средней длины пробега и увеличения скорости носителей заряда. При более высокой температуре увеличиваются хаотические тепловые колебания носителей заряда и атомов, поэтому подвижность начинает уменьшаться, но уже пропорционально температуре в степени – 3/2, т.е. ~ Т^{– 3/2}. Из рис. 3.3. видно, как влияет каждый из компонентов формулы γ = q∙N∙u на поведение электропроводности полупроводника при увеличении температуры.

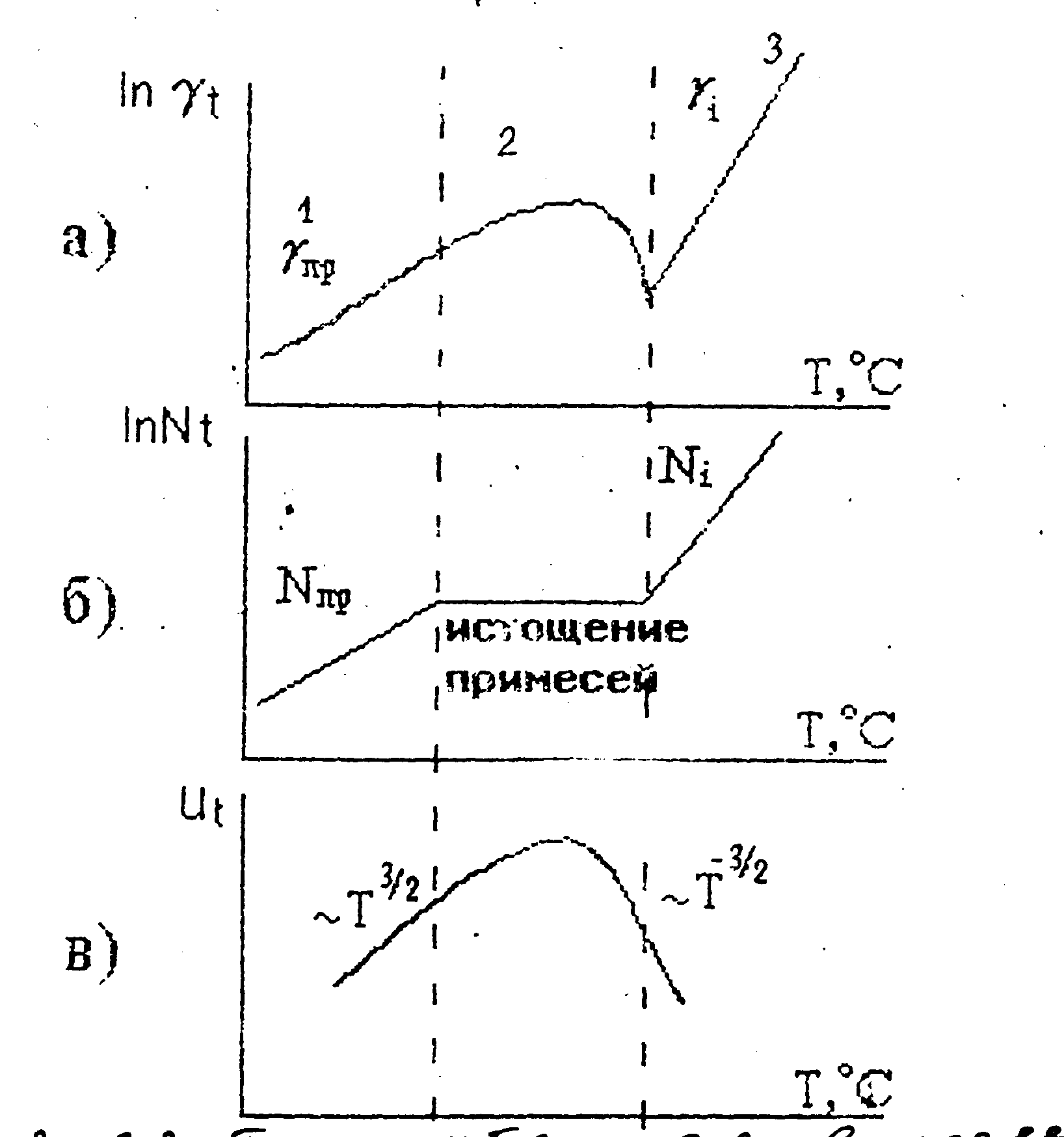
Рис. 3.3. Температурная зависимость электропроводности

Запишем формулу, отражающую зависимость концентрации носителей заряда от температуры

, (3.6)

где N_t – количество носителей заряда при данной температуре Т, м^-3;

N₀ – количество носителей при нормальных условиях (Т_комн.), м^-3;

W_t – термическая энергия активации носителей, Вт; для примесных полупроводников W_t = W_пр, для собственных – W_t = W_Д, W_Д – запрещенная зона;

К – постоянная Больцмана (К=1,38∙10^-23 Вт/град);

Т – абсолютная температура.

Подвижность носителей изменяется пропорционально температуре

, (3.7)

где u_t – подвижность носителей заряда при температуре Т, м²/В∙с.

Видим, что основное влияние на поведение электропроводности с изменением температуры оказывает концентрация носителей заряда.

Таким образом, электропроводность полупроводника от температуры изменяется экспоненциально

, (3.8)

где А – постоянная, представляющая собой электропроводность полупроводника при экстремальных условиях; это электропроводность, например, при Т = 0 К.

Так как подвижность носителей заряда изменяется с температурой незначительно, то определяет характер поведения электропроводности γ, в основном, концентрация носителей заряда N. На участке 1 (рис. 3.3) наблюдается рост примесных носителей заряда, их подвижности и примесной проводимости γ_пр; на участка 2 показано истощение примесных носителей заряда (они уже все активизированы и число не растет с ростом Т), а подвижность (U) – несколько падает. На участке 3 уже наблюдается увеличение собственных носителей заряда, способных переходить в зону проводимости из валентной зоны. На фоне быстрого роста числа носителей подвижность почти не оказывает влияния на изменение электропроводности.

Для удобства изображения зависимости γ_t и N_t, даны в полулогарифмическом натуральном масштабе, а Т – в обычном. Поэтому вместо экспонент, мы получаем зависимости в виде прямых линий (или кривых).

Таким образом, тепловая энергия способствует переходу носителей в зону проводимости (или на примесные уровни для р-типа) и электропроводность полупроводника увеличивается экспоненциально.

Температурный коэффициент сопротивления полупроводников ТКR – отрицательный, т.к. сопротивление их, как правило, с увеличением температуры уменьшается

, (3.9)

где R₁ – сопротивление полупроводника при начальной температуре Т₁;

R₂ – сопротивление при более высокой температуре Т₂.