
РЕКУРСИЯ. ПРОГРАММИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ РЕКУРСИВНЫХ ПРОЦЕДУР И |
|||
ФУНКЦИЙ. АЛГОРИТМЫ ПЕРЕБОРА С ВОЗВРАТОМ...................................................................................... |
|
1 |
|
ПОНЯТИЕ РЕКУРСИИ.................................................................................................................................... |
|
1 |
|
СТРУКТУРА РЕКУРСИВНОЙ ПРОЦЕДУРЫ..................................................................................................................... |
|
3 |
|
ПРЯМАЯ РЕКУРСИЯ.............................................................................................................................................. |
|
10 |
|
КОСВЕННАЯ РЕКУРСИЯ......................................................................................................................................... |
|
10 |
|
ОПЕРЕЖАЮЩЕЕ ОБЪЯВЛЕНИЕ............................................................................................................ |
|
10 |
|
МЕТОД ПЕРЕБОРА С ВОЗВРАТОМ.......................................................................................................... |
|
12 |
|
ДОПОЛНИТЕЛЬНО. ЗАДАЧА О ХАНОЙСКИХ БАШНЯХ................................................................. |
17 |
||
ЛИТЕРАТУРА...................................................................................................................................................... |
|
|
20 |
Рекурсия. |
Программирование |
с |
использованием |
рекурсивных процедур и функций. Алгоритмы перебора с возвратом
Понятие рекурсии
Рекурсия (от латинского recursio – возвращение) — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Вообще, рекурсивным называется любой объект, который частично определяется через себя.
Пример 1.1. Что будет делать следующая программа?
Program A; Procedure Privet; Begin
Writeln(‘Привет’); Privet
End;
Begin Privet
End.
Ответ: процедура будет бесконечно выводить на экран слово “Привет”.
Но практическое использование процедур с бесконечным самовызовом невозможно. Такая невозможность вытекает из того, что для каждой копии рекурсивной процедуры необходимо выделить дополнительную область памяти, а бесконечной памяти не существует.
1

Следовательно, главное требование к рекурсивным процедурам заключается в том, что вызов рекурсивной процедуры должен выполняться по условию, которое на каком-то уровне рекурсии станет ложным.
Если условие истинно, то рекурсивный спуск продолжается. Когда оно становится ложным, то спуск заканчивается и начинается поочередный рекурсивный возврат из всех вызванных на данный момент копий рекурсивной процедуры.
Пример 1.2. Примеры рекурсивных определений.
1.Определение факториала. С одной стороны, факториал определяется так: n!=1*2*3*...*n. С другой стороны,
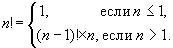 Граничным условием в данном случае является n<=1.
Граничным условием в данном случае является n<=1.
2.Определим функцию K(n), которая возвращает количество цифр
взаданном натуральном числе n: 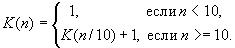
Задание. По аналогии определите функцию S(n), вычисляющую сумму
цифр заданного натурального числа. Ответ:
ì 0, если N = 0,
S(n) = í
î S(n div10) + n mod10, если n > 0
Обращение к рекурсивной подпрограмме ничем не отличается от вызова любой другой подпрограммы. При каждом рекурсивном вызове информация о нем сохраняется в специальной области памяти, называемой стеком. В стеке записываются значения локальных переменных, параметров подпрограммы и адрес точки возврата. Таким образом, какой-либо локальной переменной A на разных уровнях рекурсии будут соответствовать разные ячейки памяти, которые могут иметь разные значения. Поэтому воспользоваться значением переменной A i-ого уровня можно только, находясь на этом уровне. Информация в стеке для каждого вызова подпрограммы будет порождаться до
выхода на граничное условие. Очевидно, в случае отсутствия граничного 2
условия, неограниченный рост количества информации в стеке приведёт к аварийному завершению программы за счёт переполнения стека.
Порождение все новых вызовов рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Максимальное количество вызовов рекурсивной подпрограммы, которое одновременно может находиться в памяти компьютера, называется глубиной рекурсии. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным возвратом.
Структура рекурсивной процедуры
Структура рекурсивной процедуры может принимать три разных формы: 1) Форма с выполнением действий до рекурсивного вызова (с
выполнением действий на рекурсивном спуске):
Procedure Rec; Begin
<действия на входе в рекурсию>; If <проверка условия> then Rec [else S]
end;
Обычно проверяют, что с каждым рекурсивным вызовом значение какого-то параметра уменьшается, и это не может продолжаться бесконечно.
Пример 1.3. Вычислить значения факториала числа с выполнением
действий до рекурсивного вызова.
Program factor1; Var f,n:integer;
Procedure fact(k:integer; var S:integer);
Begin
If k>=1 then Begin
S:=k*S;
Fact(k-1,S)
End;
End;
Begin
Readln(n);
3
F:=1;
Fact(n,f);
Writeln(f) End.
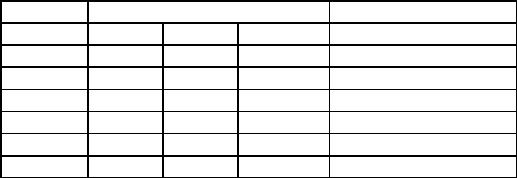
В таблице Таблица 1 показана трассировка выполнения данного алгоритма при n=3.
|
|
|
Таблица 1. Выполнение действий на рекурсивном спуске |
|
Уровень |
|
Спуск |
Возврат |
|
|
K |
S |
Fact |
|
0 |
4 |
1 |
Fact(4,1) |
24 |
1 |
4 |
4 |
Fact(3,4) |
24 |
2 |
3 |
12 |
Fact(2,12) |
24 |
3 |
2 |
24 |
Fact(1,24) |
24 |
4 |
1 |
24 |
Fact(0,24) |
24 |
5 |
0 |
|
|
|
2) Форма с |
выполнением |
действий после |
рекурсивного вызова (с |
|
выполнением действий на рекурсивном возврате):
Procedure Rec; Begin
If <проверка условия> then Rec [else S1];
<действия на выходе из рекурсии>; end;
Пример 1.4. Вычислить значения факториала числа с выполнением
действий после рекурсивного вызова.
Program factor2; Var f,n:integer;
Function fact(k:integer):integer; Begin
If k>=1 then fact:=fact(k-1)*k Else fact:=1
End;
Begin Readln(n);
Writeln(fact(n)) End.
В таблице Таблица 2 показана трассировка выполнения данного алгоритма при n=4.
4
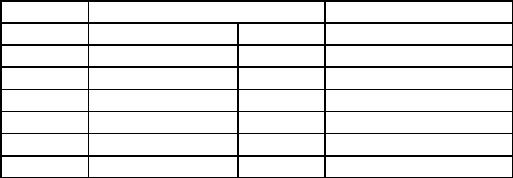
Таблица 2. Выполнение действий на рекурсивном возврате
Уровень |
Спуск |
|
Возврат |
|
K |
Fact |
|
0 |
4 |
Fact(4) |
24 |
1 |
4 |
Fact(3)*4 |
24 |
2 |
3 |
Fact(2)*3 |
12 |
3 |
2 |
Fact(1)*2 |
4 |
4 |
1 |
Fact(0)*2 |
2 |
5 |
0 |
1 |
|
3) Форма с выполнением действий как до, так и после рекурсивного вызова (с выполнением действий, как на рекурсивном спуске, так и на
рекурсивном возврате):
Procedure Rec; Begin
<действия на входе в рекурсию>; If условие then Rec;
<действия на выходе из рекурсии> end;
или
Procedure Rec; Begin
If условие then begin
<действия на входе в рекурсию>; Rec;
<действия на выходе из рекурсии> End;
end;
Пример 1.5. Вычислить значения факториала числа с выполнением
действий до и после рекурсивного вызова.
Program factor3; Var f,n:integer;
Function fact(var f:integer; k:integer):integer; Begin
f:=f*k;
If k>1 then Fact:=Fact(f,k-1)
5

Else
Fact:=f;
End;
Begin Readln(n); f:=1;
Writeln(fact(f,n)) End.
В Таблица 3 выполнена трассировка алгоритма при n=4:
Таблица 3. Выполнение действий до и после рекурсивного вызова
Уровень |
|
Спуск |
|
Возврат |
|
K |
F |
fact |
Fact |
0 |
4 |
1 |
Fact(4) |
24 |
1 |
4 |
4 |
Fact(3) |
24 |
2 |
3 |
12 |
Fact(2) |
24 |
3 |
2 |
24 |
Fact(1) |
24 |
4 |
1 |
24 |
|
|
Пример 1.5. Написать рекурсивную программу нахождения количества
цифр целого натурального числа n.
1) Выполнение действий на рекурсивном спуске: procedure K(N:longint; var kol:byte); begin
if N<10
then Kol:=Kol+1 else begin
Kol:=Kol+1;
K(N div 10, Kol); End;
end;
2) Выполнение действий на рекурсивном возврате: procedure K(N:longint; var kol:byte);
begin
if N<10
then Kol:=1 else begin
K(N div 10, Kol); Kol:=Kol+1;
6
End;
end;
или
Function K(N:Longint):Byte; Begin
If N<10
Then K:=1
Else K:=K(N div 10)+1
End;
3) Выполнение действий на рекурсивном спуске и на рекурсивном
возврате: program p1;
var n1:Longint; kol:Byte;
Function K(N:Longint; var kol:integer;):Byte; Begin
kol:=kol+1; If N<10
Then K:=kol
Else K:=K(N div 10,kol);
End; begin
readln(n1);
kol:=0;
writeln('kol=',k(n1,kol));
end.
Пример 1.6. Вычислить сумму элементов одномерного массива.
При решении задачи используем следующее соображение: сумма равна нулю, если количество элементов равно нулю, и сумме всех предыдущих
элементов плюс последний, если количество элементов не равно нулю.
Program Rec;
Type Mas = Array[1..100] Of Integer; Var A:Mas; I,N:Byte;
{Рекурсивная функция}
Function Summa(N : Byte; var A: Mas) : Integer; Begin
If N = 0
7
Then Summa := 0
Else Summa := A[N] + Summa(N - 1, A)
End;
{Основная программа} Begin
Write('Количество элементов массива? '); ReadLn(N);
Randomize;
For I := 1 To N Do Begin A[I] := -10 + Random(21); Write(A[I] : 4)
End;
WriteLn; WriteLn('Сумма: ', Summa(N, A))
End.
Пример 1.7. Определить, является ли заданная строка палиндромом, т.е. читается одинаково слева направо и справа налево.
Идея решения заключается в просмотре строки одновременно слева направо и справа налево и сравнении соответствующих символов. Если в какой-то момент символы не совпадают, делается вывод о том, что строка не является палиндромом, если же удается достичь середины строки и при этом все соответствующие символы совпали, то строка является палиндромом. Граничное условие — строка является палиндромом, если она
пустая или состоит из одного символа.
Program Palindrom;
Function Pal(S: String) : Boolean; {Рекурсивная функция}
Begin |
|
If Length(S)<=1 |
|
Then Pal:=True |
|
Else Pal:= (S[1]=S[Length(S)]) |
|
and Pal(Copy(S, 2, |
Length(S) - 2)); |
End;
Var S : String;
Begin {Основная программа}
Write('Введите строку: '); ReadLn(S);
If Pal(S)
Then WriteLn('Строка является палиндромом')
8
Else WriteLn('Строка не является палиндромом')
End.
Пример 1.8. Что будет изображено в результате выполнения
программы? program sss; uses crt;
procedure print(m,n:integer); var j:byte;
begin
for j:=1 to m do write(' ');
write('*');
for j:=1 to n do write(' ');
write('*');
for j:=1 to n do write(' ');
write('*');
writeln; end;
procedure uzor(i:integer); begin
if i=4 then begin write('*******'); writeln end else begin
print((i-1),3-i); uzor(i+1); print((i-1),3-i)
end;
end; begin
clrscr;
uzor(1); end.
Ответ: снежинка
** *
* * *
9
