МНМ2012_Задания_Дифференциальное исчисление

Индивидуальные задания №2 Дифференциальное исчисление

Задание Д 1. Продифференцировать данные функции.

Задание Д 2. Продифференцировать данные функции.

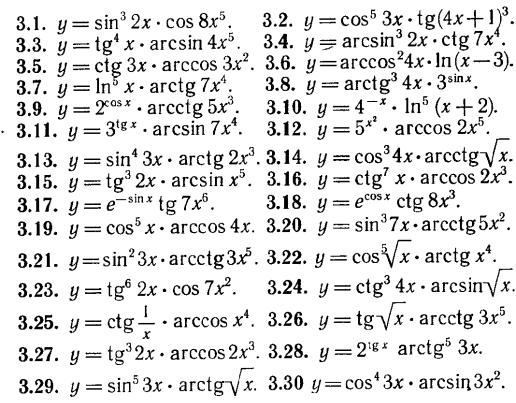
Задание Д 3. Продифференцировать данные функции.

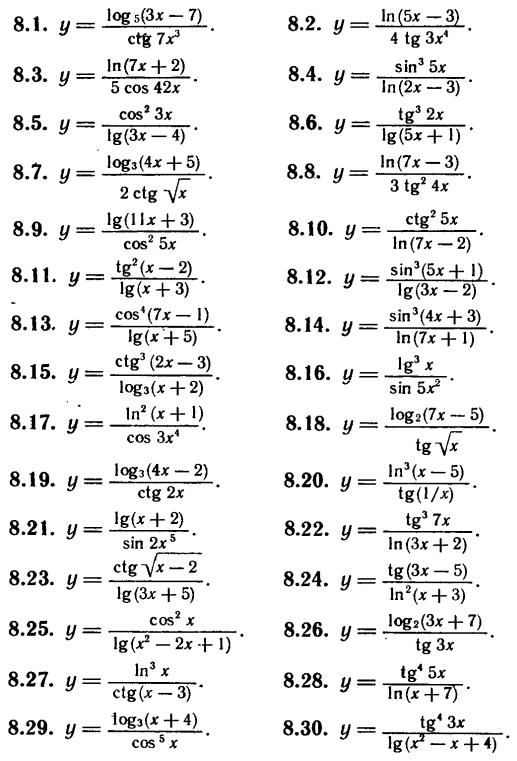
Задание Д 8. Продифференцировать данные функции.

Задание Д 14. Продифференцировать данные функции.

Задание Д 23. Для данной функции y и аргумента х0 вычислить y'''(х0) и построить кубическое приближение y(х) в окрестности т. х0, используя ряд

Задание Д 24. Решить следующие задачи.

24.1.

24.2.

24.3.

24.4.

24.5.

24.6.

24.7.

24.8.

24.9.

24.10.

24.11.

24.12.

24.13.

24.14.

24.15.

24.16.

24.17.

24.18.

24.19.

24.20.

24.21.

24.22.

24.23.

24.24.

24.25.

24.26.

24.27.

24.28.

24.29.

24.30.

Задание Л1. Найти указанные пределы, используя правило Лопиталя.

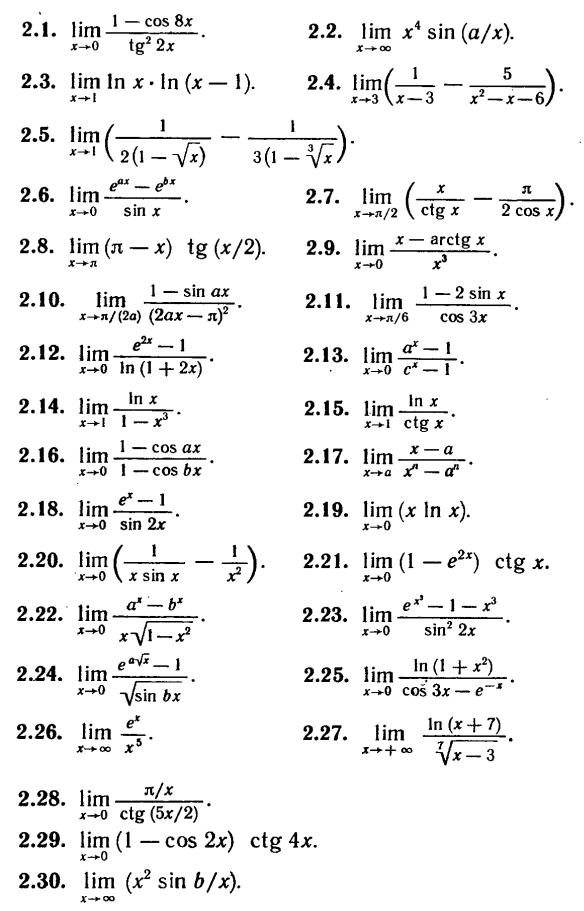
Задание Л2. Найти указанные пределы, используя правило Лопиталя.

Задание Ф 1. Провести полное исследование указанных функций и построить их

график.

Ф1.1. y = 3 – 9x + 6x2 – x3. Ф1.2. y = –1 + 9x – 6x2 + x3 . Ф1.3. y = 3 + 9x + 6x2 + x3. Ф1.4. y = 5 + 18x + 12x2 + 2x3 .

Ф1.5. y = –3 + 18x – 12x2 + 2x3 . Ф1.6. y = –35 + 48x – 18x2 + 2x3.

Ф1.7. y = 37 + 48x + 18x2 + 2x3. Ф1.8. y = 7 + 27x + 18x2 + 3x3.

Ф1.9. y = –5 + 27x – 18x2 + 3x3 . Ф1.10. y = 7 – 27x + 18x2 – 3x3 .

Ф1.11. y = 53 + 45x + 12x2 + x3 . Ф1.12. y = –51 + 45x – 12x2 + x3 .

Ф1.13. y = 53 – 45x + 12x2 – x3 . Ф1.14. y = 111 + 72x + 15x2 + x3.

Ф1.15. y = –109 + 72x – 15x2 + x3 . Ф1.16. y = –17 + 24x – 9x2 + x3 . Ф1.17. y = 19 + 24x + 9x2 + x3 .

Ф1.18. y = 19 – 24x + 9x2 – x3 . Ф1.19. y = 4 + 5x – 3x2 + x3/3.

Ф1.20. y = –2 + 5x + 3x2 + x3/3 .

Ф1.21. y = –2 – 5x + 3x2 – x3/3. Ф1.22. y = –8/3 + 3x + x2 – x3/3 . Ф1.23. y = 14/3 + 3x – x2 – x3/3.

Ф1.24. y = –8/3 –3x + x2 + x3/3 . Ф1.25. y = 14/3 – 3x – x2 + x3/3. Ф1.26. y = –13/3 + 12x – 4x2 + x3/3. Ф1.27. y = 19/3 + 12x + 4x2 + x3/3. Ф1.28. y = 19/3 – 12x + 4x2 – x3/3 .

Ф1.29. y = –8 –9x + 3x2 + x3. Ф1.30. y = 14 – 9x – 3x2 + x3.