Материал презентаций по физике / Часть 2 / Лекция 5 / Лекция 5

8

Лекция 5

Проводники в электрическом поле

Вопросы

1. Проводники в электростатическом поле.

2. Электроемкость заряженного проводника. Конденсаторы.

3. Энергия заряженного проводника, конденсатора и электростатического поля.

1. Проводники в электростатическом поле

Проводником называется среда, в которой имеется достаточное число свободных электрических зарядов. Например, в металлах в 1 см³ содержится около 10²³ свободных электронов. В диэлектриках свободных электронов менее 10⁶ в 1 см³, а в хороших диэлектриках менее 10³ в 1 см³.

Хорошими проводниками электрического тока являются не только металлы, но еще растворы электролитов и ионизованные газы.

Металлы имеют кристаллическую структуру. В узлах кристаллических решеток металлов находятся положительно заряженные ионы, а валентные электроны могут свободно передвигаться между ними в различных направлениях по всему объему. Совокупность свободных электронов в металле называют электронным газом.

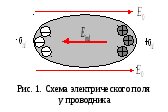
Если проводник поместить в электрическое поле, то свободные электроны перемещаются внутри него под действием поля против силовых линий, пока результирующее поле внутри металла не станет равным нулю. В результате под действием внешнего электри­чес­кого поля на поверхности пластины появятся индуцированные заряды с поверхностны­ми плотностями и . Электрическое поле индуцированных зарядов компенсирует внешнее электрическое поле, т.е.

, т.к. , то  , (1)

т.е. электростатическое поле внутри проводника отсутствует, а потенциал проводника является постоянным (проводник эквипотенциален).

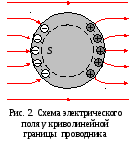
У криволинейной поверхности проводника силовая линия напряженности электростатического поля должна быть направлена по нормали к этой поверхности, иначе под действием тангенциальной составляющей поля заряды перемещались бы по проводнику, что противоречит условию (1).

В заряженном проводнике избыточный заряд располагается только на поверхности, т.к. согласно теореме Гаусса для замкнутой области S внутри проводника заряд отсутствует.

_{. (2)}

Пример. Точечный заряд у поверхности Земли. Поскольку силовые линии перпендикулярны эквипотенциальным поверхностям, электрическое поле вблизи проводника должно быть нормально к его поверхности. (Это понятно, так как если бы поле имело касательную составляющую, то электроны двигались бы вдоль поверхности проводника). В качестве примера на рис. 3 показано электрическое поле точечного заряда вблизи поверхности Земли (Земля – проводник).

_{Электростатическая индукция}

_{При внесении незаряженного проводника в электростатическое поле носители зарядов приходят в движение. Перераспределение идет до тех пор, пока внутри проводника не будет Е=0, а на поверхности Е=Еn.}

_{Явление, состоящее в электризации незаряженного проводника во внешнем электростатическом поле путем разделения в этом проводнике уже имеющихся в нем в равных количествах положительных и отрицательных зарядов, называется электризацией через влияние или электростатической индукцией.}

_{Индуцированные заряды появляются на проводнике вследствие смещения их под действием поля. При замыкании концов проводника с разноименными зарядами может появиться ток смещения, поэтому вектор на поверхности проводника называется вектором электрического смещения .}

. (2)

Электростатическая защита

Э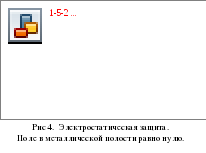лектростатическая защита объектов (например, приборов) от влияния внешних электростати­чес­ких полей основана на том, что заря­ды располагаются на поверхности, а полость в замкнутом проводнике не заряжена (экранирована от внеш­него поля). Для электростатической защи­ты можно использовать не сплошной проводник, а метал­лическую сетку, которую заземляют, т.е. соединяют с нулевым потенциалом Земли.

Свойство зарядов распола­гать­ся на внешней поверхности исполь­зуется в электростатических генераторах, применяемых в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

2. Электроемкость заряженного проводника. Конденсаторы

Электроемкостью заряженного проводника называется скалярная физическая величина С, характеризующая способность проводника накапливать заряды и численно равная заряду, изменяющему потенциал проводника на один Вольт.

, 1 Фарад = 1 Кулон / 1 Вольт . (3)

Так как заряды в проводнике располагаются только на поверхности, то электроемкость не зависит от материала проводника, его агрегатного состояния, но зависит от формы и размеров.

Фарад – большая единица. Например, используя потенциал проводящей поверхностно заряженной сферы и формулу (3), получим

_,

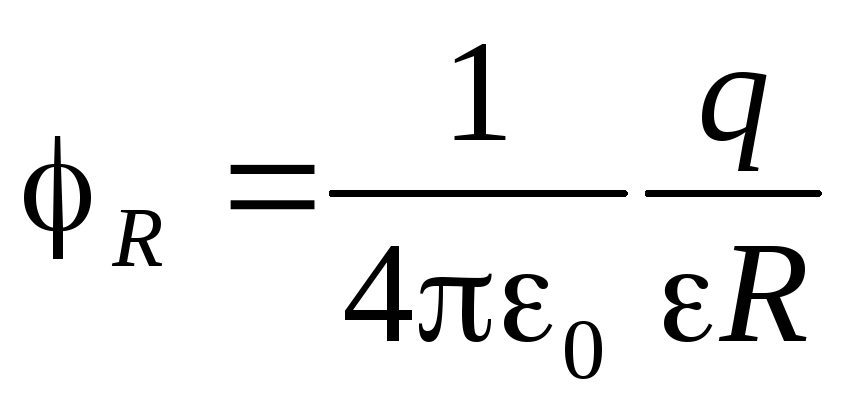
_{что в 1400 раз больше радиуса Земли. Электроемкость Земли - 711 мкФ.}

Единицы измерения в технике:

1 мФ = 10^-3Ф; 1 мкФ = 10^-6Ф; 1 нФ = 10^-9Ф; 1 пФ = 10^-12Ф.

Конденсатором называется система из двух изолированных друг от друга проводников. Эти проводники обычно называют пластинами, хотя они могут иметь любую форму. На практике конденсаторы используются как «накопители зарядов» или «резервуары», в которых содержится энергия электрического поля. Если на пластины поместить одинаковые по величине, но противоположные по знаку заряды и , то между пластинами возникнет разность потен­циа­лов . Емкостью конденсатора называется величина:

. (4)

Плоский конденсатор

; ;

, (5)

т.е. ёмкость конденсатора зависит только от его геометрических характеристик, вида диэлектрика между пластинами, и не зависит от сообщаемых ему зарядов.

Для того чтобы получить заданную емкость, можно использовать не один, а несколько конденсаторов. Систему из нескольких конденсаторов называют батареей конденсаторов. Емкостью батареи конденсаторов называется величина

,

где - полный заряд батареи, полученный от источника, а - напряжение, поданное на батарею конденсаторов.

Параллельное соединение конденсаторов

При параллельном соединении конден­саторов между собой соединены все положительные и отрицательные обкладки. В этом случае все конденсаторы заряжаются до одной и той же разности потенциалов , общий заряд такой батареи:

и, следовательно, емкость всей системы:

. (6)

Ёмкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов. При С₁ = С₂ = С₃ = 1 С₀ = 3.

Последовательное соединение конденсаторов

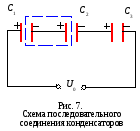
При последовательном соединении кон­ден­саторов отрицательная обкладка первого конденсатора соединена с положи­тельной обкладкой второго и т. д. В этом случае на всех кон­ден­са­торах заряды одинаковы:

,

а выделенная часть цепи нейтральна, так как она не соединена с источником напряжения.

Общее напряжение на батарее конденсаторов складывается из напряжений на каждом конденсаторе:

.

Из-за равенства зарядов

. (7)

При С₁ = С₂ = С₃ = 1 С₀ = 1/3, т.е. ёмкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.

3. Энергия заряженного проводника, конденсатора

и электростатического поля

Для зарядки проводника нужно совершить работу против сил кулоновского отталкивания одноименных зарядов.

Если незаряженному проводнику сообщать заряд малыми порциями dq, переносимыми из бесконечности, где ₀=0. По мере зарядки проводника ёмкостью его потенциал возрастает

.

Энергия заряженного проводника равна совершенной работе

. (8)

При зарядке конденсатора малыми порциями по аналогии с зарядкой проводника имеем энергию заряженного конденсатора

. (9)

Используя формулу (9), можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. При изменении расстояния x между пластинами эта сила совершает работу

_.

Выразим энергию (9) через характеристики электростатического поля

, ,

- объём между обкладками конденсатора.

. (10)

Объёмная плотность энергии

.

Используя связь (2) между напряженностью электрического поля и вектором электрического смещения полученный результат можно записать так:

. (11)

Объемная плотность энергии конденсатора уже не зависит от каких-либо его геометрических характеристик. Она выражается лишь через характеристики электрического поля конденсатора. Таким образом, энергия конденсатора – это энергия электрического поля, заключенного между его обкладками.

Выражение (11) для плотности электрического поля в какой-либо точке пространства, доказанное нами в случае электрического поля конденсатора, является универсальным. В общем случае энергия неоднородного электрического поля, заключенная в некотором объеме V, рассчитывается через объемный интеграл:

, (12)

т.е. носителем энергии является электростатическое поле.