PGTU / 5 семестр / Надежность / Задачник_Тема 4

Тема 4. ПОКАЗАТЕЛИ НАДЁЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ

Расчет надежности систем с восстановлением принципиально отличается от расчета невосстанавливаемых систем, вплоть до показателей надежности. Критерии надежности систем с восстановлением изложены в пп.2.3.1. учебного пособия.

Функционирование восстанавливаемого объекта представляет собой последовательность чередующихся интервалов работоспособности и восстановления.

Для определения характеристик надежности с восстановлением необходимо описать поток отказов, поток восстановлений и их взаимодействие. Рассмотрим данные потоки по отдельности, а также комплексные характеристики, их связывающие.

Характеристикой потока отказов является параметр потока отказов :

, (4.1)

где – число изделий, отказавших за момент времени t, - общее число изделий.

Параметр потока отказов, определяемый как отношение числа изделий, отказавших в единицу времени, к числу испытываемых изделий, представляет собой интенсивность, или плотность потока.

Между интенсивностью отказов невосстанавливаемой системы и параметром потока отказов восстанавливаемой системы могут быть установлены следующие соотношения:

1. Если увеличивается, то > .

2. Если уменьшается, то < .

3. Если = const, то = .

Третье соотношение описывает важный частный случай, характерный для периода нормальной работы, когда = const. В этом случае параметр потока отказов ω можно считать численно равным интенсивности отказов λ, а поток отказов будет пуассоновским, т.е. простейшим, ординарным, стационарным потоком без последствий, в этом случае

λ=1/Т_о. (4.2)

Поток восстановления для рассматриваемой системы может характеризоваться параметром потока восстановления , представляющим интенсивность этого потока. Физический смысл – вероятность восстановления в течение достаточно малого отрезка времени. Если поток восстановлений также рассматривать как пуассоновский, то является величиной, обратной среднему времени восстановления :

. (4.2)

Потоки отказов и восстановлений описывают процесс функционирования объекта с двух сторон независимо друг от друга. Для связи потока вводятся комплексные показатели, в качестве которых используются обычно коэффициент готовности и коэффициент оперативной готовности .

Коэффициент готовности – это вероятность застать объект исправным в произвольно выбранный момент времени t. Для простейших потоков

. (4.3)

Коэффициент оперативной готовности – это вероятность того, что объект, будучи исправным в момент t, проработает безотказно в течение времени . вычисляют как произведение вероятности застать объект исправным в момент на вероятность безотказной работы в течение оставшегося интервала времени:

. (4.4)

Формула (4.3) определяет коэффициент готовности в установившемся состоянии, так называемый стационарный коэффициент готовности. Однако в момент включения системы начинается переходный процесс, который продолжается некоторое время до перехода системы в установившееся состояние. Рассмотрим, как рассчитывается переходный процесс для простейшего случая – система состоит из одного элемента.

Пусть необходимо оп­ределить надежность изделия, не имею­щего резервирования, с заданными интен­сивностями переходов – па­раметров по­тока отказов  = const и интенсивностью восстановления . Р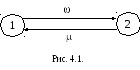аботоспособность сис­темы описывается графом (рис. 4.1), принципы построения которого описаны в пп.2.3.2 и в данном задачнике будут рассмотрены в следующей теме: состояние 1 – состояние работоспособности, состояние 2 – состояние от­каза. P₁ - вероятность пребывания системы в состоянии 1, P₂ - вероятность пребывания системы в состоянии 2.

Описание графа по правилу, приведенному в 2.3.2, дает следующую систему уравнений:

Учитывая, что в момент включения t = 0 система должна быть ис­правна (), получаем:

Отсюда

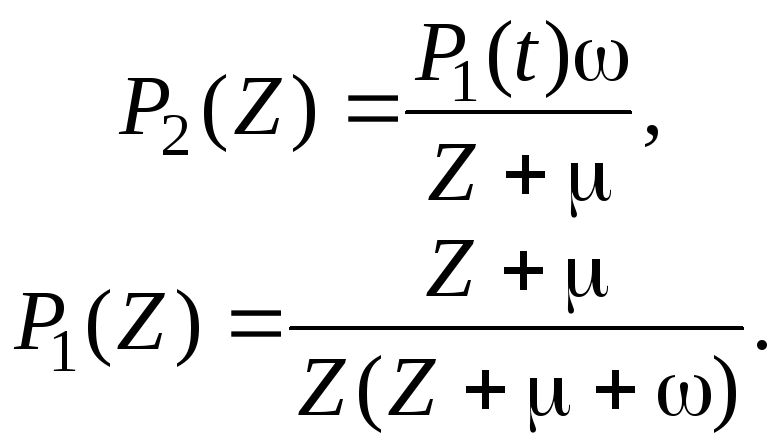
Обратное преобразование вероятности требует приведения ее к табличному виду. Для этого умножим и разделим на ( + ):

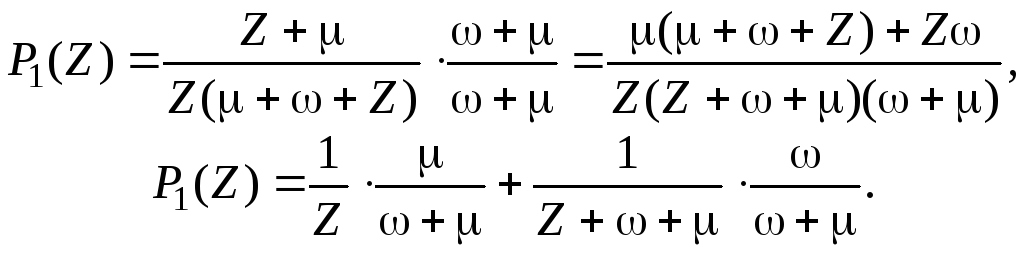
Отсюда, учитывая, что 1/Z соответствует 1(t), а соответст­вует , получаем:

Анализом полученного выражения устанавливаем, что при t не может быть ниже величины . Эта постоянная часть и явля­ется стационарным коэффициентом готовности изделия:

Постоянная времени экспоненты . Переходный про­цесс длится 34 Т_пэ, после чего наступает установившийся режим.

Пример. Пусть ω=0,25 ч^-1. = 0,95 ч^-1. Построим график зависимости коэффициента готовности восстанавливаемого элемента от времени.

Сначала сведём результаты вычислений в таблицу:

t,ч	Кг(t)	t,ч	Кг(t)
0	1	3	0,796
0,5	0,905	3,5	0,793
1	0,853	4	0,792
1,5	0,824	4,5	0,791
2	0,809	5	0,791
2,5	0,800	5,5	0,790
		6	0,790

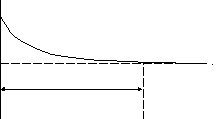
По данным таблицы построим график (рис. 4.2).

K_Г

1

0,9

0,8 0,79

0,7

время переходного процесса

0,6 t, ч

1 2 3 4 5

Рис. 4.2.

Таким образом, коэффициент готовности в установившемся режиме равен 0,79. Время переходного процесса около 4 часов.

Варианты для самостоятельных и расчетных работ.

Задание: построить график зависимости коэффициента готовности восстанавливаемого элемента от времени и определить время переходного процесса, если заданы параметр потока отказов ω и интенсивность потока восстановления .

1. ω =10^-1 ч^-1, = 0,3 ч^-1.

2. ω =10^-1 ч^-1, = 0,4 ч^-1.

3. ω =10^-1 ч^-1, = 0,5 ч^-1.

4. ω =10^-1 ч^-1, = 0,6 ч^-1.

5. ω =10^-1 ч^-1, = 0,7 ч^-1.

6. ω =10^-1 ч^-1, = 0,8 ч^-1.

7. ω =10^-1 ч^-1, = 0,9 ч^-1.

8. ω =10^-1 ч^-1, = 1 ч^-1.

9. ω =0,15 ч^-1, = 0,3 ч^-1.

10. ω =0,15 ч^-1, = 0,4 ч^-1.

11. ω =0,15 ч^-1, = 0,5 ч^-1.

12. ω =0,15 ч^-1, = 0,6 ч^-1.

13. ω =0,15 ч^-1, = 0,7 ч^-1.

14. ω =0,15 ч^-1, = 0,8 ч^-1.

15. ω =0,15 ч^-1, = 0,9 ч^-1.

16. ω =0,15 ч^-1, = 1 ч^-1.

17. ω =0,05 ч^-1, = 0,3 ч^-1.

18. ω =0,05 ч^-1, = 0,4 ч^-1.

19. ω =0,05 ч^-1, = 0,5 ч^-1.

20. ω =0,05 ч^-1, = 0,6 ч^-1.

21. ω =0,05 ч^-1, = 0,7 ч^-1.

22. ω =0,05 ч^-1, = 0,8 ч^-1.

23. ω =0,05 ч^-1, = 0,9 ч^-1.

24. ω =0,05 ч^-1, = 1 ч^-1.

25. ω =0,07 ч^-1, = 0,5 ч^-1.

26. ω =0,07 ч^-1, = 0,6 ч^-1.

27. ω =0,07 ч^-1, = 0,7 ч^-1.

28. ω =0,07 ч^-1, = 0,8 ч^-1.

29. ω =0,07 ч^-1, = 0,9 ч^-1.

30. ω =0,07 ч^-1, = 1 ч^-1.