PGTU / 5 семестр / Надежность / Задачник_Тема 5

Тема 5. РАСЧЁТ НАДЁЖНОСТИ ВОССТАНАВЛИВАЕМЫХ

СИСТЕМ

В данной теме рассматривается метод расчета надежности, основанный на составлении графа переходов изделия в различные состояния работоспособности (графа работоспособности). Этот метод приведен в пп.2.3.2 и 2.3.4 учебного пособия.

На первом этапе составляется граф работоспособности объекта. Для этого определяются все состояния работоспособности с учетом блоков системы и устанавливаются интенсивности переходов по данным состояниям. Например, для системы с восстановлением из двух блоков (рис. 2.19), один из которых резервный, могут быть выделены следующие состояния:

1. Блок 1 и блок 2 исправны (система полностью исправна).

2. Блок 1 отказал, блок 2 исправен.

3. Блок 2 отказал, блок 1 исправен.

4. Отказ блока 1 и блока 2 (отказ системы).

Вероятность нахождения системы в i-м выделенном состоянии обозначается Р_i. Вероятность перехода из i состояния в j – Р_ij. Например, Р₁₂ – вероятность отказа первого блока, Р₂₁ – вероятность восстановления первого блока и т.д.

Граф работоспособности системы (см. рис. 5.1), построенный с учетом введенных обозначений, представлен на рис. 5.2.

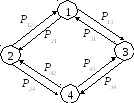
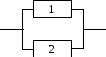
Рис. 5.1. Рис. 5.2.

Вероятности вследствие ординарности потока равны нулю. Поясним данное утверждение на примере. Для того, чтобы система перешла из состояния 1 в состояние 4, необходимо, чтобы в один момент времени произошли два события – отказали как блок 1, так и блок 2. Но это противоречит понятию ординарности, разрешающему в один момент времени происходить только одному событию.

На втором этапе по графу работоспособности составляют систему уравнений.

Поскольку в данной теме мы рассматриваем только статический коэффициент готовности, то пропускаем этап составления системы дифференциальных уравнений и сразу переходим к системе линейных уравнений. Существует следующее правило составления системы. В левой части каждого уравнения записывается 0. В правой части уравнения содержится столько членов, сколько стрелок связано (входит и выходит) с данным состоянием. Каждый член равен произведению интенсивности потока , переводящего систему по данной стрелке, умноженной на вероятность того состояния, откуда стрелка исходит. Если стрелка входит в описываемое состояние, то произведению присваивается знак «+», если исходит, то знак «-».

Для графа, приведенного на рис.5.2., получается следующая система уравнений

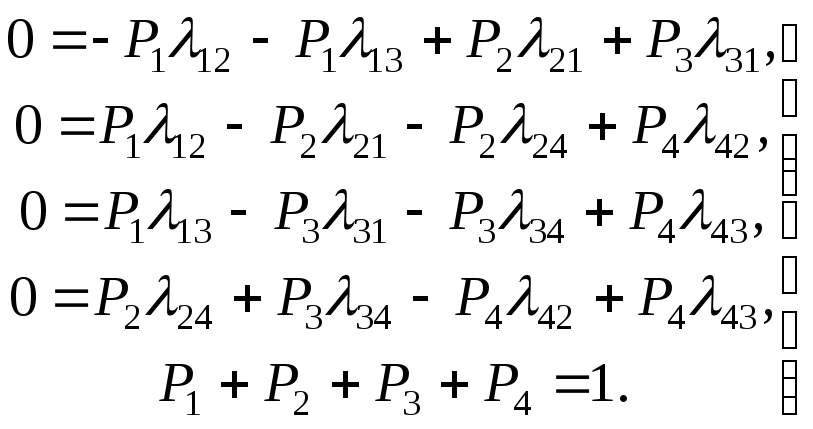(5.1)

Добавление последнего уравнения является обязательным и необходимым для закрытия системы, поскольку ни одно из предыдущих уравнений не учитывает начальных условий.

На третьем этапе уравнения системы решаются, и находятся искомые вероятности пребывания объекта в состояниях его работоспособности.

На четвертом этапе рассчитывается коэффициент работоспособности как сумма вероятностей работоспособных состояний. В рассматриваемом примере три работоспособных состояния, следовательно, коэффициент готовности будет вычисляться по формуле

(5.2)

Пример 1. Определить коэффициент готовности, если система состоит из двух блоков, соединённых последовательно, параметр потока отказов блока =0,01, параметр потока восстановления блока =1 ч^-1. Ремонт осуществляет один ремонтник.

Этап 1: построим граф работоспособности системы. Поскольку надежностные характеристики блоков 1 и 2 одинаковые, можно уменьшить число состояний. Построенный граф работоспособности системы приведен на рис. 5.3.,где 0 – состояние работоспособности (оба блока исправны); 1- отказал любой из двух блоков (отказ системы); 2 – отказали оба блока (отказ системы.)

2w w

Рис. 5.3.

Этап 2: запишем для этого графа систему линейных уравнений:

Этап 3: из первого уравнения

Из третьего уравнения

Тогда

Подставляя эти значения в четвёртое уравнение, получаем

Этап 4:

Пример 2. Определить коэффициент готовности, если система состоит из двух блоков, соединённых параллельно, параметр потока отказов блока =0,01, параметр потока восстановления блока =1 ч^-1. Ремонт блоков системы осуществляют два ремонтника после выхода из строя всей системы.

Этап 1: построим граф переходов системы (рис. 5.4), где 0 – состояние работоспособности (оба блока исправны); 1- состояние работоспособности (один из блоков неисправен); 2 – оба блока неисправны (отказ системы). При построении данного графа было нарушено соглашение об ординарности потока восстановлений (стрелка между 2 и 0 состояниями), однако такое нарушение позволяет точнее промоделировать ситуацию, поскольку на правтике система будет включена только после того, как будут отремонтированы оба блока.

2w w

2

Рис.5.4

Этап 2: запишем для этого графа систему линейных уравнений:

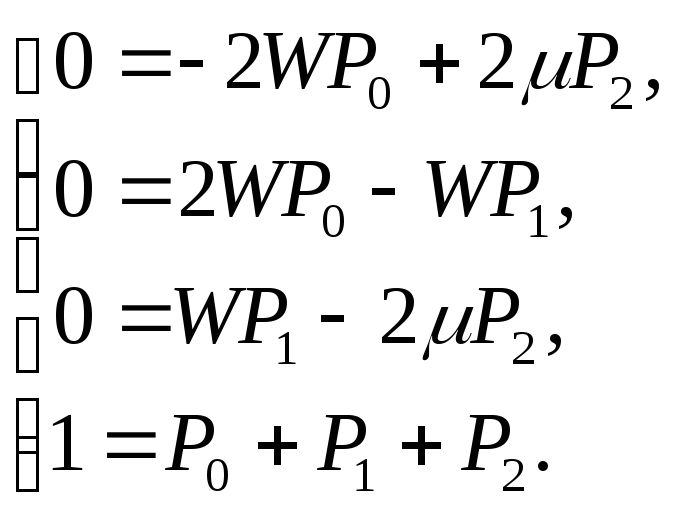
Этап 3: из второго уравнения

Из третьего уравнения

Тогда

Подставляем эти значения в четвёртое уравнение:

Этап 4:

Варианты для самостоятельных и расчетных работ.

Задание 1. Определить коэффициент готовности, если система состоит из трех блоков, соединенных последовательно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт системы осуществляет один ремонтник.

1. = 10^-1 ч^-1 , = 0,2 ч^-1.

2. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 2. Определить коэффициент готовности, если система состоит из трех блоков, соединенных последовательно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт системы осуществляют два ремонтника.

3. = 10^-1 ч^-1 , = 0,2 ч^-1.

4. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 3. Определить коэффициент готовности, если система состоит из трех блоков, соединенных последовательно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт системы осуществляют три ремонтника.

5. = 10^-1 ч^-1 , = 0,2 ч^-1.

6. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 4. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляет один ремонтник сразу же по выходе любого блока из строя.

7. = 10^-1 ч^-1 , = 0,2 ч^-1.

8. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 5. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляется же по выходе любого блока из строя, одним ремонтником – по выходе из строя одного блока, двумя ремонтниками - по выходе из строя двух или трех блоков.

9. = 10^-1 ч^-1 , = 0,2 ч^-1.

10. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 6. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляется же по выходе любого блока из строя, одним ремонтником – по выходе из строя одного блока, двумя ремонтниками - по выходе из строя двух блоков и тремя ремонтниками по выходе из строя всех трех блоков.

11. = 10^-1 ч^-1 , = 0,2 ч^-1.

12. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 7. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляет один ремонтник после выхода из строя всей системы.

13. = 10^-1 ч^-1 , = 0,2 ч^-1.

14. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 8. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют два ремонтника после выхода из строя всей системы.

15. = 10^-1 ч^-1 , = 0,2 ч^-1.

16. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 9. Определить коэффициент готовности, если система состоит из трех блоков, соединенных параллельно, параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют три ремонтника после выхода из строя всей системы.

17. = 10^-1 ч^-1 , = 0,2 ч^-1.

18. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 10. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.5. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляет один ремонтник сразу после выхода из строя любого блока.

Рис.5.5.

19. = 10^-1 ч^-1 , = 0,2 ч^-1.

20. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 11. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.5. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют два ремонтника сразу после выхода из строя любого блока.

21. = 10^-1 ч^-1 , = 0,2 ч^-1.

22. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 12. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.5. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют три ремонтника сразу после выхода из строя любого блока.

23. = 10^-1 ч^-1 , = 0,2 ч^-1.

24. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 13. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.6. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляет один ремонтник сразу после выхода из строя любого блока.

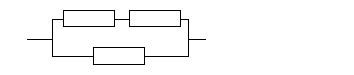
Рис.5.6.

25. = 10^-1 ч^-1 , = 0,2 ч^-1.

26. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 14. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.6. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют два ремонтника сразу после выхода из строя любого блока.

27. = 10^-1 ч^-1 , = 0,2 ч^-1.

28. = 10^-1 ч^-1 , = 0,6 ч^-1.

Задание 15. Определить коэффициент готовности, если система состоит из трех блоков, который соединены, как показано на рис5.6. Параметр потока отказов блока , параметр потока восстановления блока . Ремонт блоков системы осуществляют три ремонтника сразу после выхода из строя любого блока.

29. = 10^-1 ч^-1 , = 0,2 ч^-1.

30. = 10^-1 ч^-1 , = 0,6 ч^-1.