Задания на 3 семестр / Физико-технические эффекты_ФТЭ / Задачи

№1

1.Определить напряжение в стержнях, если второй стержень нагрет на , при этом считать, что сила P отсутствует. Модуль упругости материала стержней , коэффициент линейного расширения .

2. Вычислить напряжения в стержнях при совместном действии допускаемой силы [P] и нагрева.

№2

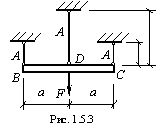
Пусть дана система, представленная на рисунке. Предположим, что все стержни выполнены из одного материала и имеют одинаковую площадь поперечного сечения А. Примем, что внешняя нагрузка отсутствует, т.е. F = 0, но средний стержень нагрет на величину =10⁰С

№3

Определить напряжения, возникающие в упругих элементах системы (см. рис.), если после монтажа температура увеличилась на °C. Дано: А₁/А₂ = 2, Е = 200 ГПа, .

№4

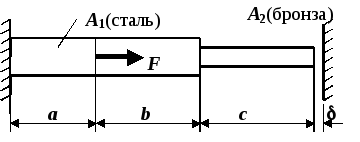
Стержень переменного сечения с заданным соотношением площадей поперечного сечения , выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой существует зазор .

Требуется:

Найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру =20⁰С и проверить прочность стержня от температурного воздействия.

№5

Для схемы, изображенной на рис.1 необходимо:

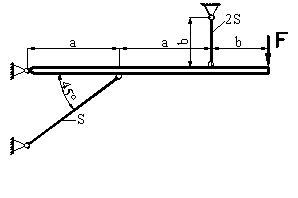
Рис.1

1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную или неравнополочную сталь, при условии, что поперечное сечение одного из стержней в два раза больше, чем другого.

2) Определить напряжения в стержнях:

- от действия силы F;

- от неточности монтажа, если считать, что один из стержней выполнен короче на величину ;

- от изменения температуры.

3) Определить суммарные напряжения от действия внешних сил, от неточности монтажа и от изменения температуры.

4) Подсчитать недонапряжения или перенапряжения в стержнях.

№6

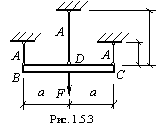
Пусть дана система, представленная на рисунке. Предположим, что все стержни выполнены из одного материала и имеют одинаковую площадь поперечного сечения А. Примем, что внешняя нагрузка отсутствует, т.е. F = 0, но средний стержень нагрет на величину =5⁰С

№7

Пусть дана система, представленная на рисунке. Предположим, что все стержни выполнены из одного материала и имеют одинаковую площадь поперечного сечения А. Примем, что внешняя нагрузка отсутствует, т.е. F = 0, но средний стержень нагрет на величину =15⁰С

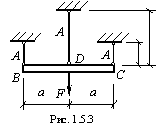
№8

Стержень переменного сечения с заданным соотношением площадей поперечного сечения , выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой существует зазор .

Требуется:

Найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру =10⁰С и проверить прочность стержня от температурного воздействия.

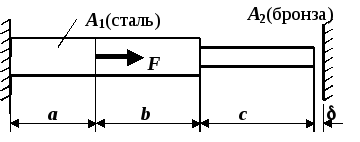
Рис.1

№9

Стержень переменного сечения с заданным соотношением площадей поперечного сечения , выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой существует зазор .

Требуется:

Найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру =15⁰С и проверить прочность стержня от температурного воздействия.

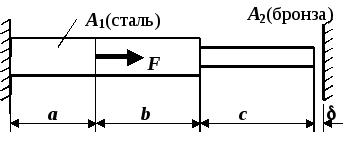
Рис.1

№10

Требуется:

1.Определить напряжение в стержнях, если второй стержень нагрет на ∆t=10⁰C, при этом считать, что сила P отсутствует. Модуль упругости материала стержней , коэффициент линейного расширения .

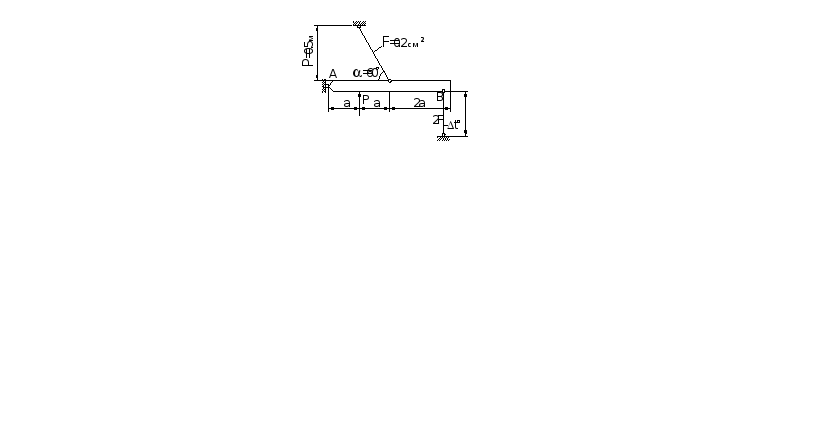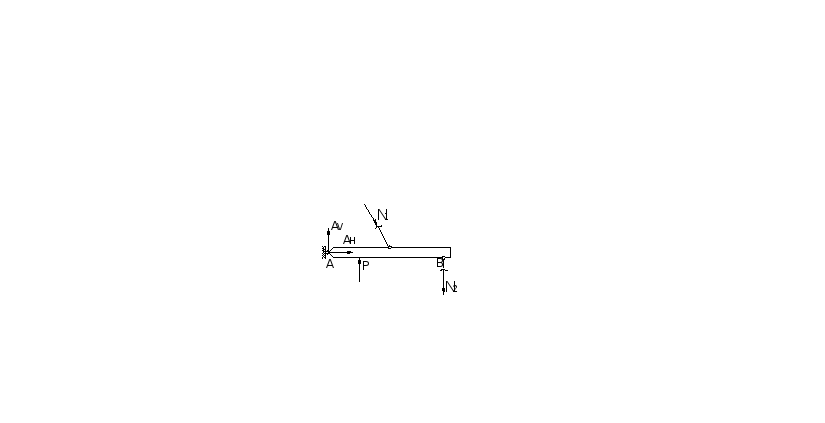а) б) в)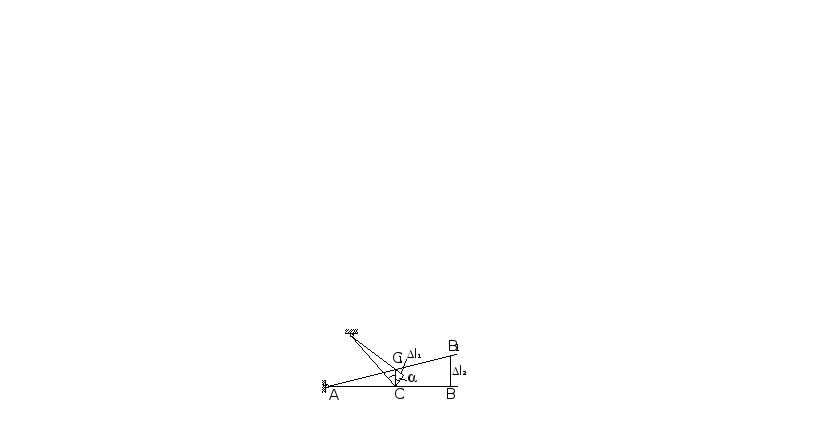

№11

В городе площадью 400 км² за 10 мин во время ливневого дождя выпало 20 мм воды. Подсчитайте энергию и мощность выделения тепла от слияния капель во время дождя, если капли, достигшие поверхности Земли, имели диаметр 3 мм, а образовались из мелких капель диаметром 3 ·10^-3 мм.

№12

Смачиваемый водою кубик массы m = 20 г плавает на поверхности воды. Ребро кубика имеет длину a = 3 см. На каком расстоянии от поверхности воды будет находиться нижняя грань кубика?

№13

Капля воды равномерно падает в воздухе. Найдите разность между радиусом кривизны поверхности капли в ее верхней точке и радиусом кривизны в нижней точке, расстояние между которыми h = 2,3 мм.

№14

Между двумя горизонтальными стеклянными пластинками находится капля ртути в форме лепешки радиуса R и толщины h. Считая, что h << R, найдите массу m груза, который надо положить на верхнюю пластинку, чтобы расстояние между пластинками уменьшилось в n раз. Краевой угол θ. Вычислите m, если R = 2,0 см, h = 0,38 мм, n = 2, θ = 135°.

№15

Из круглого отверстия вытекает вертикальная струя воды так, что в одном из горизонтальных сечений ее диаметр d = 2,0 мм, а в другом сечении, расположенном ниже на l = 20 мм, диаметр струи в n = 1,5 раза меньше. Найти объем воды, вытекающий из отверстия за одну секунду.

№16

Между двумя горизонтальными стеклянными пластинками находиться капля ртути в форме лепешки радиусом R и толщиной h.Считая, что h<<R, найти массу m груза, который надо положить на верхнюю пластинку, чтобы расстояние между пластинками уменьшилось в n раз. Краевой угол θ. Вычислить m, если R=2см, h=0,38 мм, n=2 и θ=135 градусов.

№17

Два стеклянных диска радиуса R = 5,0 см смочили водой и сложили вместе так, что толщина слоя воды между дисками h = 1,9 мкм. Считая смачивание полным, найти силу, которую нужно приложить перпендикулярно к плоскости дисков, чтобы оторвать их друг от друга.

№18

Вертикальный капилляр привели в соприкосновение с поверхностью воды. Какое количество тепла выделится при поднятии воды по капилляру? Смачивание считать полным, поверхностное натяжение равно σ=0,073 Н/м.

№19

В дне сосуда со ртутью имеется круглое отверстие диаметра d=0,5 мм. При какой максимальной толщине слоя ртути она еще не будет вытекать через это отверстие?

№20

Два стеклянных диска радиуса R=0,1мм смочили водой и сложили вместе так, что толщина слоя воды между дисками h=0,05 мм. Считая смачивание полным, найти силу, которую нужно приложить перпендикулярно к плоскости дисков, чтобы оторвать их друг от друга.

№21

Какую часть от абсолютной сорбции составляет избыточная сорбция,

если в результате сорбции концентрация сорбата увеличилась в 25 раз?

№22

Какую часть от абсолютной сорбции составляет избыточная сорбция,

если в результате сорбции концентрация сорбата увеличилась в 17 раз?

№23

Сорбция растворенного в воде ПАВ на поверхности ртуть-вода подчиняется уравнению Ленгмюра. При концентрации ПАВ 0.1 моль/л степень заполнения поверхности составляет 1. Рассчитайте поверхностное натяжение ртути на границе с раствором при 298 К и концентрации ПАВ в растворе 0.1 моль/л. Предельное значение площади, занимаемой молекулой ПАВ на поверхности S₀=0.2 Нм², поверхностное натяжение ртути на границе с водой составляет 0.373 Дж/м².

№24

Адсорбция растворенного в воде ПАВ на поверхности ртуть-вода подчиняется уравнению Ленгмюра. При концентрации ПАВ 0.2 моль/л степень заполнения поверхности составляет 0.5. Рассчитайте поверхностное натяжение ртути на границе с раствором при 298 К и концентрации ПАВ в растворе 0.1 моль/л. Предельное значение площади, занимаемой молекулой ПАВ на поверхности S₀=0.2 Нм², поверхностное натяжение ртути на границе с водой составляет 0.373 Дж/м².

№25

Какую часть от абсолютной сорбции составляет избыточная сорбция,

если в результате сорбции концентрация сорбата увеличилась в 15 раз?

Определить по уравнению Ленгмюра сорбцию пропионовой кислоты,

поверхностное натяжение раствора, которой равно 55.6 кДж/м².

Концентрация кислоты в растворе 0.5 моль/л, коэффициент b в уравнении

Ленгмюра 7.73 л/моль, поверхностное натяжение воды при 295 К 71.96

кДж/м².

№27

Определить по уравнению Ленгмюра сорбцию пропионовой кислоты,

поверхностное натяжение раствора, которой равно 66.5 кДж/м².

Концентрация кислоты в растворе 0.1 моль/л, коэффициент b в уравнении

Ленгмюра 7.73 л/моль, поверхностное натяжение воды при 295 К 71.96

кДж/м².

№28

При адсорбции углекислого газа на активированном угле были получены следующие данные:

р·10-2, Н/м2	9,9	49,7	99,8	200
А·103,кг/кг	32,0	70,0	91,0	102,0

Графически определите константы в уравнении Лэнгмюра, пользуясь которыми, постройте изотерму Лэнгмюра.

№29

Какую часть от абсолютной сорбции составляет избыточная сорбция,

если в результате сорбции концентрация сорбата увеличилась в 20 раз?

№30

Какую часть от абсолютной сорбции составляет избыточная сорбция,

если в результате сорбции концентрация сорбата увеличилась в 12 раз?

№31

Если газ проникает через пористую перегородку между двумя сосудами, в других отношениях изолированных друг от друга и от окружающей среды, то значении энтальпии до начала процесса равно значению энтальпии Н₂ после окончания процесса. Происходящее при этом изменение температуры определяется коэффициентом Джоуля — Томсона .

а) Показать, что

и, следовательно,

б) Показать, что

в) Убедиться, что j = 0 для идеального классического газа.

г) Показать, что для газа Ван-дер-Ваальса,

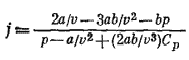
д) Получить уравнение кривой, отделяющей на р-v-диаграмме область j>0 от области j<0, для газа Ван-дер-Ваальса. Эта кривая носит название кривой инверсии. [Расширение ведет к охлаждению только для состояний, лежащих в области j>0.]

е) Показать, что для газа Ван-дер-Ваальса давление, соответствующее максимуму кривой инверсии, есть

Р_i0 = 9р_c,

№32

В эксперименте Джоуля — Томсона газ, заключенный в трубку с адиабатическими стенками, протекает при стационарных условиях через пористую перегородку из области с высоким давлением в область низкого давления, причем давления по обе стороны пористой перегородки поддерживаются постоянными (фиг. 32). В результате этого температуры по обе стороны перегородки различны. Доказать, что в этом эксперименте энтальпия остается постоянной, и выразить через С_р и (dV/dT)_p величину (dТ/dр)_н, определяющую изменение температуры (коэффициент Джоуля — Томсона). Кроме того, для тех случаев, когда в достаточно хорошем приближении уравнепие состояния можно записать в виде pV = RT + В(Т)р, выразить коэффициент Джоуля — Томсона через В.

Рис.3 – Иллюстрация к задаче.

№33

Вычислить коэффициент Джоуля — Томсона (dТ/dр)_н для разреженного газа Ван-дер-Ваальса с точностью до второго порядка по nb/V («1) и na/VRT («1). Кроме того, определить температуру Т_i, при которой коэффициент Джоуля — Томсона обращается в нуль, и выразить ее через критическую температуру Тс = 8а/27Rb.

№34

Tpубкa, заполненная кислородом, разделена пористой перегородкой две камеры (рис.6). С помощью равномерного перемещения поршней в левой камере поддерживается давление Р_A, a в правой—давление Р_B < Р_A.

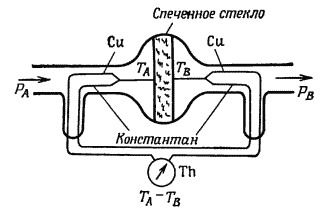
Рис. 6 - Схема установки для наблюдения эффекта Джоуля — Томсона.

Термопары включены навстречу друг другу, поэтому прибор Th показывает разность температур T_A – T_B.

При этом газ перетекает из левой камеры в правую через отверстия в перегородке. Скачала объем левой камеры равен V_А, а объем правой равен нулю. В конце процесса объем правой камеры становится равным V_В > V_А, а объем левой — равным нулю. Предполагается, что система теплоизолирована. Вычислить изменение температуры при следующих начальных значениях параметров: Р_А = 250 ат, Р_B= I ат, Т_А = 273 К. Считать используемый газ – кислород - газом Ван-дер-Ваальса. Для поправок Ван-дер-Ваальса использовать значения а =1,40 ат∙м⁶/кмоль², b = 0,032 м³/кмоль.

№35

Показать, что в процессе Джоуля — Томсона энтропия газа увеличивается.

Решение:

Для вычисления изменения энтропии газа заменим реальный процесс Джоуля — Томсона квазистатическим изэнтальпическим процессом, переводящим систему в то же конечное состояние. Для такого процесса dl = = TdS + VdP = 0, а потому

Учитывая, что давление в процессе Джоуля — Томсона понижается, заключаем отсюда, что энтропия S возрастает.

№36

Сосуд с твердыми адиабатическими стенками разделен на две части твердой адиабатической перегородкой. По одну сторону перегородки находится газ, по другую — вакуум. Вывести общую термодинамическую формулу для температуры газа, которая установится в нем после удаления перегородки. Применить полученную формулу к идеальному газу и показать, что в этом случае изменения температуры не произойдет.

№37

С помощью уравнения состояния Дитеричи р = nRT (V — nb)^-1 eхр (—na/RTV) определить зависимость температуры инверсии для эффекта Джоуля — Томсона от давления и изобразить ее графически. Использовать закон соответственных состояний и выразить значения давления, температуры и объема через критические величины. Провести такое же рассмотрение для газа Ван-дер-Ваальса.

№38

Чтобы получить абсолютную температуру, нужно прокалибровать эмпирическую температуру θ, измеренную с помощью газового термометра (при постоянном давлении). Для этого необходимо при фиксированном давлении определить зависимость от θ плотности ρ, теплоемкости и коэффициента Джоуля — Томсона. Вывести основную формулу, необходимую для такой калибровки.

№39

Значения коэффициента Джоуля — Томсона для воздуха с давлением 1 кг/см² приведены в таблице. Плотность воздуха ρ аппроксимируется формулой

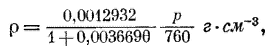
где р — давление в мм рт. ст. и θ — температура в ⁰С. В интервале температур от 0 до 100⁰С удельная теплоемкость при постоянном давлении почти не меняется и равна 0,240 кал∙г^-1∙град^-1. С помощью этих данных определить численное значение 0⁰С в абсолютной температурной шкале.

№40

Найти кривую инверсии дифференциального эффекта Джоуля — Томсона для газа, подчиняющегося уравнению Дитеричи.

№41

В самолетной гидравлической системе отключение потребителя производится электромагнитным краном. Кран полностью перекрывает трубопровод за время t_закр=0,02 сек.

Определить повышение давления перед краном в момент отключения потребителя при следующих данных (рис. 1).

Длина трубопровода от крана до гидроаккумулятора, где гасится ударное давление, l=4 м, диаметр трубопровода 12 мм, толщина его стенки δ=1 мм, материал — сталь (E=2,2 • 10⁶ кГ/см²); объемный модуль упругости жидкости АМГ-10 K=13 300 кГ/см², ее плотность ρ = 90 кГсек²/м⁴; скорость потока в трубе v₀=4,5 м/сек.

№42

Определить величину повышения давления в стальной водопроводной трубе, если скорость воды в трубе до удара была v=1 м/с, диаметр трубы d=0,5 м и толщина стенок δ=0,005 м.

№43

В стальном трубопроводе длиной l=200 м, диаметром d=0,2 м и толщиной стенок δ = 5∙10^-3 м расход воды Q=0,1 м3/с. Расчетная температура воды 20°С. Определить наименьшее время закрывания задвижки τ_мин, чтобы повышение давления в конце трубопровода, вызванное гидравлическим ударом, было не более Δр_макс= 4∙10³ Па = 400 кПа. Чему будет равно повышение давления в случае мгновенного закрывания задвижки в трубопроводе?

№44

В конце системы, состоящей из двух последовательно соединенных стальных трубопроводов, установлена задвижка. Определить повышение давления перед задвижкой при ее закрывании, если время закрывания τ=0,2 с. Расход воды Q=0,02 м³/с; диаметры трубопроводов. d₁ = 0,2 м, d₂ = 0,1 м; длина: l₁= 100 м, l₂=200 м. Определить наименьшее время закрывания задвижки, исключающее прямой гидравлический удар. Толщина стснок трубопроводов δ=5∙ 10^-3 м. Температура воды 20°С.

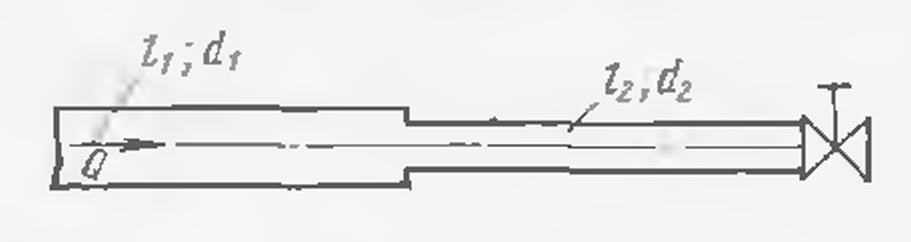
№45

Из круглого отверстия вытекает вертикальная струя воды так, что в одном из горизонтальных сечений ее диаметр d = 2,0 мм, а в другом сечении, расположенном ниже на l = 20 мм, диаметр струи в n = 1,5 раза меньше. Найти объем воды, вытекающий из отверстия за одну секунду.

№46

Вода в количестве Q перекачивается по чугунной трубе диаметром d, длиной l c толщиной стенки . Свободный конец трубы снабжён затвором. Определить время закрытия затвора при условии, чтобы повышение давления в трубе вследствие гидравлического удара не превышало Па. Как повысится давление при мгновенном закрытии затвора?

Q =0,053 м³/с. d = 0,15м , l = 1600м , = 9,5 мм , = 1 000 000 Па, =1000 кг/м³.

№47

На рис.4 показана модель водопровода. Из поднятого на некоторую высоту h резервуара, играющего роль водонапорной башни, выходит магистральная труба постоянного сечения S и длины l. Эта труба заканчивается узкой загнутой вверх трубкой сечения S₁ с краном, при открывании которого из трубки бьет фонтан.

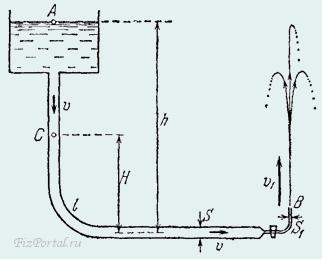
Рис.3 – Иллюстрация к задаче

1. С какой скоростью бьет вода из фонтана и на какую максимальную высоту  онаподнимается? 2. С какой скоростью движется вода в магистральной трубе и каково там  давление? 3. Какое давление будет в магистральной трубе при мгновенном перекрывании крана? 4. Как будет зависеть от времени давление в том случае, когда кран  закрывается постепенно в течение промежутка времени τ?

№48

По стальному трубопроводу длиной l=250 мм, диаметром d=50 мм и толщиной стенок =3,5 мм перекачивается вода с расходом Q=4 л/с.

Определить повышение давления в трубопроводе, если время закрывания задвижки равно =1c.

№49

По стальному трубопроводу длиной l=250 мм, диаметром d=50 мм и толщиной стенок =3,5 мм перекачивается вода с расходом Q=4 л/с.

Найти максимально допустимое давление для данного трубопровода, если допустимое напряжение стенок на разрыв

№50

По стальному трубопроводу длиной l=250 мм, диаметром d=50 мм и толщиной стенок =3,5 мм перекачивается вода с расходом Q=4 л/с.

Исходя из максимально допустимого повышения давления Р_макс =700 кПа, определить минимально допустимое время закрытия задвижки.

№51

Рассчитать (в первом приближении) размеры рабочего колеса центробежного насоса ЖРД ракеты- ФАУ-2 и определить необходимое давление на входе в насос из условия отсутствия кавитации по следующим данным: нагнетаемая жидкость — этиловый спирт (75%), γ=864 кГ/см³, h₁ = 44 мм рт. ст.; весовой расход (подача насоса) G=56 кГ/сек; давление, создаваемое насосом, Р_нас=20,7 ат; число оборотов рабочего колеса n=3800 об/мин.

№52

Требуется определить предельно допустимую скорость течения воды в отводе, если давление воды в трубопроводе перед отводом р₁ = 1,2∙10⁵ Па, температура воды 80°С, критическое число кавитации для отвода х_кр=2.

№53

Требуется определить предельно допустимую скорость течения воды в отводе, если давление воды в трубопроводе перед отводом р₁ = 2∙10⁵ Па, температура воды 60°С, критическое число кавитации для отвода х_кр=2.

№54

Определить критическое число кавитации х_кp при движении жидкости в трубопроводе с регулирующим клапаном, если коэффициент местного сопротивления клапана ζ=1.

№55

Определить критическое число кавитации х_кp при движении жидкости в трубопроводе с регулирующим клапаном, если коэффициент местного сопротивления клапана ζ=1,5. По полученной величине определить тип потока.

№56

Определить предельно допустимую безкавитационтую скорость движения воды в стальном трубопроводе v_пр перед регулирующим клапаном при температуре 20°С, если коэффициент местного сопротивления клапана ζ=1. Диаметр трубопровода d=0,05 м, расстояние от входа в трубопровод до клапана l=10 м, давление на входе в трубопровод р₀ =10⁵ Па.

№57

Рассчитать число кавитации для потока воды температурой 80⁰С протекающем при давлении Р=5∙10⁴ Па со скоростью 2м/с.

№58

Рассчитать число кавитации для потока воды температурой 60⁰С протекающем при давлении Р = 2∙10⁴ Па со скоростью 1 м/с.

№59

Определить кавитационный запас насоса, перекачивающего воду при температуре 20⁰ С. Давление во входном патрубке р_в= 2∙10⁴ Па, скорость потока v_в=1 м/с.

№60

Определить кавитационный запас насоса, перекачивающего воду при температуре 50⁰ С. Давление во входном патрубке р_в= 5∙10⁴ Па, скорость потока v_в=0,5 м/с.

№61

Рассчитать величину акустоэдс индуцированную звуковой волной на концах проводника CdS , если коэффициент поглащения звука α=30 , коэфициент электронного поглощения звука =2,59 , равновесная концентрация электронов

n0 = 5*, длина проводника L= 1 см,   интенсивность звука на входе образца I₀ =1вт/см, подвижность электронов μ = 200см/В*с, скорость звука =1,8*10см/с.

№62

Оценить коэффициент поглощения Г для распространения попереч­ного звука в CdS. Если скорость звука = 1,8 *10см/с, x=0.036, деформация измеряется с частотой ω=3*10с-1, величина волнового вектора звука q=1.7*10, время релаксации τ=3.5*10^-9c, радиус экранирования R =1.6*10см