5.2. Постулаты Бора

Предположение Бора заключалось в том, что классическая электромагнитная теория просто неприменима к электрону, движущемуся вокруг ядра. Он предположил, что два члена в формуле Бальмера представляют собой полные энергии электрона на двух «разрешенных» орбитах в атоме водорода. Если умножить обе части формулы Бальмера на hи ввести обозначения , то можно написать

hν =E_n –E_m.

Бор предположил, что энергия электрона не теряется на излучение, когда он движется по любой из разрешенных орбит.

Электрон излучает энергию только тогда, когда он совершает переход между двумя разрешенными орбитами.

Энергия испущенного фотона в точности равна разности энергий электрона на этих орбитах.

Чтобы доказать правильность этих предположений, Бор попытался вычислить энергии этих состояний. Оказалось, что можно получить ряд дискретных разрешенных значений энергии «на орбитах» только при том предположении, что момент импульса квантуется, т.е. меняется скачком. В итоге в основу своей теории Бор положил два постулата.

Первый постулат Бора(постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергию. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

m_evr_n=nħ, (n= 1, 2, 3, …), (5.3)

где m_eмасса электрона,v его скорость наn-й орбите. Стационарные состояния соответствуют дискретному (прерывному) ряду дозволенных значений энергииE_n.

Второй постулат Бора(правило частот): при переходе электрона с одной стационар­ной орбиты на другую излучается (поглощается) один фотон с энергией

hν=E_nE_m(5.4)

Энергия фотона равна разности энергий соответствующих стационарных состояний (Е_nиЕ_m —соот­ветственно энергии стационарных состояний атома до и после излучения (поглоще­ния)). ПриE_m<E_nпроисходит излучение фотона (переход атома из состояния с боль­шей энергией в состояние с меньшей энергией. ПриЕ_m>Е_n его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту.

Набор возможных дискретных частот ν =(E_n  E_m)/hквантовых перехо­дов и определяет линейчатый спектр атома. Величинаnназывается главным квантовым числом.

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем – систем, состоящих из ядра с зарядом Zeи одного электрона (например, ионы Не⁺, Li²⁺).

Решая совместно уравнение второго закона Ньютона для электрона

F_k=ma_n, 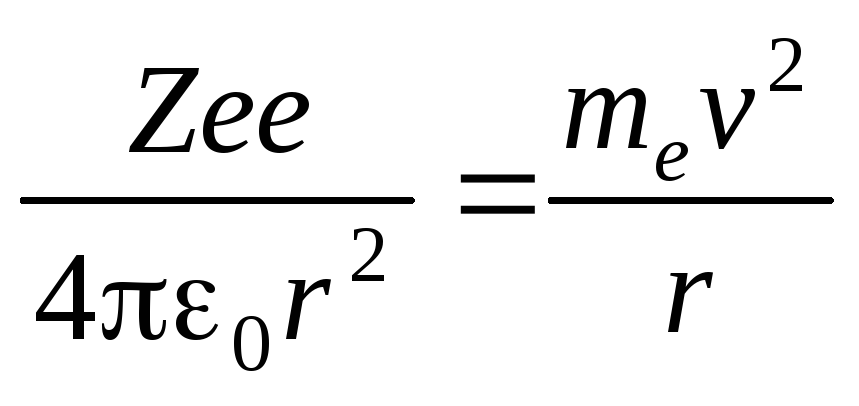, (5.5)

(где m_е иv масса и скорость электрона на орбите радиусаr; ε₀электрическая постоянная; F_k– кулоновская сила) и уравнение (5.3), получим выраже­ние для радиусаn-й стационарной орбиты:

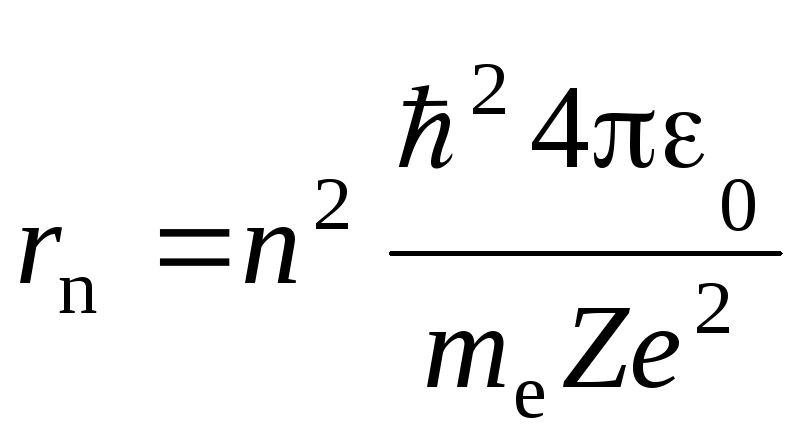, гдеn = 1, 2, 3, ... . (5.6)

Для атома водорода (Z= 1) радиус первой орбиты электрона приn =1, называемыйпервым боровским радиусом(r₁ =а), равен

.

Полная энергия электрона в водородоподобной системе складывается из его кине­тической энергии (mv² /2) и потенциальной энергии в электростатическом поле ядра (qφ = –Ze²/(4πε₀r)

, (5.7)

(при этом учли, что ).

Подставляя квантованные для радиуса n-й стационарной орбиты значения (5.6) в (5.7), получим, что энергия электрона может прини­мать только следующие дозволенные дискретные значения:

, (n = 1, 2, 3, …), (5.8)

где знак минус означает, что электрон находится в связанном состоянии.

Из формулы (5.8) следует, что энергетические состояния атома образуют после­довательность энергетических уровней, изменяющихся в зависимости от значения n.Целое числоnв выражении (5.8), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние сn= 1 являетсяосновным(нормальным)состоянием; состояния сn >1 являются возбужденными.Энер­гетический уровень, соответствующий основному состоянию атома, называется основ­ным (нормальным) уровнем; все остальные уровни являются возбужденными.

Придавая nразличные целочисленные значения, получим для атома водорода (Z= 1), согласно формуле (5.8), возможные уровни энергии. Энергия атома водорода с увеличениемnвозрастает, и энергетические уровни сближаются. Атом водорода обладает, таким образом, минимальной энергией (E₁= – 13,55 эВ) приn= 1 и максимальной (E_max = 0) приn = ∞. Следовательно, значениеE_max= 0 соответствует ионизацииатома (отрыву от него электрона).

Согласно второму постулату Бора (5.3), при переходе атома водорода (Z= 1) из стационарного состоянияn в стационарное состоя­ниет с меньшей энергией испускается квант

,

откуда частота излучения

. (5.9)

Подставляя в формулу (5.9) m = 1 и n = 2, 3, 4, ..., получим группу линий, образующих серию Лаймана и соответствующих переходам электро­нов с возбужденных уровней (n = 2, 3, 4, ...) на основной (m = l). Аналогично, при подстановке т = 2, 3, 4, 5, 6 и соответствующих им значений n = 3, 4, 5, 6, 7 получим серии Баль­мера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 5.2).

Теория Бора была первым шагом в создании квантовой механики. Дальнейшее развитие атомной физики показало справедливость постулатов Бора не только для атомов, но и для других микроскопических систем – для молекул и атомных ядер. Эта часть теории Бора сохранилась при дальнейшем развитии квантовой теории. Иначе обстоит дело с моделью атом Бора, основанной на рассмотрении движения электрона в атоме по законам классической механики при наложении дополнительных условий квантования. Вскоре выяснилось, что электронам присущи свойства, не согласующиеся с представлением о планетарном их движении.