Дифракция на дифракционной решетке

Рассмотрим дифракцию на одномерной дифракционной решетке, так как этот вид дифракции находит широкое применение во многих методах спектрального анализа.

Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей, ле­жащих в одной плоскости и разделенных непрозрачными промежутка­ми, равными по ширине. Изготавливается пу­тем нанесения параллельных штрихов на поверхность стекла с помощью делительных машин. Эти места являются, таким об­разом, практически непрозрачными промежутками между неповрежден­ными частями пластинки, которые играют роль щелей. Число штрихов на 1 мм определяется областью спектра исследуемого излучения – от 300 мкм в инфракрасной области до 1200 мкм – в ультрафиоле­товой).

Итак, имеется система из N параллельных щелей с шириной каждой цели a и расстоянием между соседними щелями b (рис. 2.6). Сумма a + b = d называется периодом, или постоянной дифракцион­ной решетки. На решетку нормально падает плоская монохроматичес­кая волна. Требуется исследовать интенсивность света, распростра­няющегося в направлении, составляющем угол φ с нормалью к пло­скости решетки.

Кроме распределения ин­тенсивности света вследствие дифракции на каждой щели, нужно учесть интерференцию между N пучками (пере­распределение световой энергии за счет интерфе­ренции волн от N щелей  когерентных источников). Очевидно, минимумы будут на прежних местах, ибо ус­ловие минимума дифракции для всех щелей одинаково. Эти минимумы называются главными минимумами. Они соответствуют таким углам φ , для которых А_φ = 0, т.е. свет от разных частей каждой щели полно­стью гасится. В этом на­правлении ни одна щель не дает света. Условие главных минимумов совпадает с условием (2.6).

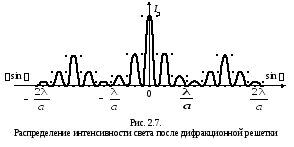
К главным минимумам, создаваемым каждой щелью в от­дельности, добавляются минимумы, возникающие в результате интерфе­ренции света, прошедшего через различные щели. Появляются добавоч­ные минимумы в областях дифракционных максимумов. Внешне это про­является в том, что широкие полосы, создаваемые одной узкой щелью, покрываются рядом более тонких полос, вызванных интерференцией лучей, исходящих от разных щелей: первой и второй, первой и треть­ей и т.д. Чем больше щелей, тем больше добавочных минимумов может возникнуть. Так как общий световой поток остается неизменным, про­исходит усиление световых потоков около направлений, удовлетворя­вших условиям максимумов при интерференции от разных щелей за счет уменьшения световой энергии в других направлениях. На рис. 2.7 для примера показано распределение интенсивности света и расположение максимумов иминимумов в случае двух щелей.

Воспользуемся методом Френеля. В одном и том же направлении все щели излучают свет совершенно одинаково. Результат интерференции зависит от оптической разности хода в сходственных точках двух соседних щелей до точки С_-φ, на экране. Для всех сходствен­ных точек эта разность хода одинакова и равна d sin φ. Если

, (2.7)

колебания от соседних щелей взаимно усиливают друг друга, и в точке С_-φ наблюдается максимум ди­фракции. Амплитуда суммарного колебания в этих точках экрана максимальна:

А_max ≈ NA_φ,

где A_φ  амплитуда колебания, посылаемого одной щелью под уг­лом φ.

Интенсивность главного максимума

, (2.8)

поэтому формула (2.7) определяет положение главных максимумов интен­сивности. Число k дает порядок главного максимума. Максимум ну­левого порядка один и расположен в точке С₀; максимумов первого, второго и т.д. порядков по два и расположены они симметрично от­носительно С₀ , на что указывает знак "±".

Кроме главных максимумов, имеется большое число более слабых побочных максимумов, разделенных добавочными минимумами. Побочные максимумы значительно слабее главных максимумов. Расчет показывает, что ин­тенсивность побочных максимумов не превышает 1/23 интенсивности ближайшего главного максимума. В главных максимумах амплитуда суммарного колебания в N раз, а интенсивность в N² раз больше, чем в соответствующем месте дает одна щель. Увеличение максимумов происходит также за счет того, что в случае решетки отдельные яркие главные максиму­мы разделены темными областями добавочных минимумов и очень слабых побочных максимумов. В итоге происходит резкое сужение, ди­фракционных максимумов (пропорционально ~ 1/N), которые стано­вятся тонкими и яркими. Такие яркие линии, четко локализованные в пространстве, легко обнаруживаются и могут быть использованы для спектроскопических исследований.

По мере удаления от центра экрана интенсивность дифракцион­ных максимумов убывает (увеличивается расстояние от источников). Поэтому не удается наблюдать все возможные дифракционные макси­мумы.

Заметим, что количество дифракционных максимумов, даваемых решеткой по одну сторону от центра экрана, определяется условием φ = π/2  максимальный угол дифракции; sin φ < 1, откуда с учетом (2.8)

. (2.9)

При этом не следует забывать, что k  целое число.

Положение главных максимумов зависит от длины волны λ. Поэтому при освещении дифракционной решетки белым светом все максимумы, кроме центрального (k = 0), разложатся в спектр, обращенный фиолетовым концом к центру дифракционной картины. Та­ким образом, дифракционная решетка может служить для исследова­ния спектрального состава света, т.е. для определения частот (или длин волн) и интенсивности всех его монохроматических компонент. Применяемые для этих целей приборы называются дифракционными спектрографами, если исследуемый спектр регистрируется с помощью фотопластинки, и дифракционными спектроскопами, если спектр на­блюдается визуально.

Угловая дисперсия дифракционной решетки

Качество дифракционной решетки определяется двумя характери­стиками: угловой дисперсией (D) и разрешающей силой (разрешающей спо­собностьюR).

Основное назначение дифракционной ре­шетки  установление длины волны исследуемого излучения. Так как положение спектральных линий задается углом, определяющим направление лучей (см. уравнение (2.7)), целесообразно ввести угловую дисперсию D:

, (2.10)

где ∆φ  угловое расстояние между спектральными линиями, отли­чающимися по длине волны на ∆λ (рис.2.8); D  угловое расстояние между двумя линиями, отличающимися по длине волны на 1 (1=10^-10 м).

Дифференцируя (2.7) слева по φ, а справа по λ, находим, что , откуда

.

Чем меньше период решетки d и чем выше порядок спектра k , тем больше угловая дисперсия. В пределах небольших углов (cos φ ~1 ) можно положить

. (2.11)

Из выражения (2.11) следует, что угловая дисперсия прямо пропорциональна порядку дифракции k и обратно пропорциональна рас­стоянию между соседними штрихами (периодом решетки) d . Следовательно, для увеличения дисперсии необходимо увеличивать число штрихов на единицу длины. Этим объясняется необходимость изготавливать дифракцион­ные решетки с возможно большим числом штрихов на 1 мм ее ширины.

Разрешающая сила дифракционной решетки

Большая дисперсия оптических приборов (в том числе дифракционной решетки) является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ₁ и λ₂ могут наблюдаться как два само­стоятельных или как один максимум. Как видно из рис. 2.9, при одинаковой угловой дисперсии линий λ₁ и λ₂ возможность их разре­шения (раздельного восприятия) различна. Так, на рис. 2.9 слева мини­мум между линиями λ₁ и λ₂ , отсутствует, и эти линии не разли­чаются как самостоятельные, а на рис. 2.9 справа имеются наблюдаемые минимумы между линиями λ₁ и λ₂.

Чтобы охарактеризовать способность прибора при данной дис­персии различать две близлежащие линии, вводится понятие разре­шающей силы R. Для количественной характеристики этого понятия нужно ввести критерий разрешения. Согласно Рэлею, две близлежащие спектральные линии с равными интенсивностями и симметричными одинаковыми контурами разрешимы, если максимум одной длины волны λ₁, совпадает с минимумом дру­гой и наоборот. При удовлетворении этого усло­вия интенсивность «провала» между максимумами составляет 80 % интенсивности каждой линии, что является достаточным для раздель­ного наблюдения линий λ₁ и λ₂. Нарушение кри­терия Рэлея приводит к наблюдению одной линии вместо двух.

Если разность длин волн | λ₂ – λ₁ | между двумя соседними максимумами, для которых выполняется критерий Рэлея, обозначить через ∆λ , а среднюю длину волны, соответствующую центру прова­ла между максимумами, – через λ, то в качестве количественной характеристики разрешающей силы мож­но взять величину

. (2.12)

Таким образом, разрешающей силой R дифракционной решетки называется величина, обратная минимальной раз­ности длин волн ∆λ (взятой около некоторой длины волны λ), которые разделены (разрешены) данной решет­кой. Согласно условию Рэлея, а также (2.7) разре­шение линий имеет место при

R = k N, (2.12)

где k  порядок дифракционного максимума; N  общее число щелей решетки.

Из выражения (2.12) видно, что чем больше число щелей решетки N , тем больше её разрешающая си­ла (разрешающая способность). При заданном числе щелей R увеличивается при переходе к спектрам высших порядков. Современные дифракционные решетки обладают до­вольно высокой разрешающей способностью (до 210⁵ ).

Дифракция на пространственной решетке

Дифракция света наблюдается не только на плоской одномерной решетке, но и на двумерной решетке (штрихи нанесены во взаимно перпендикулярных направлениях) в одной и той же плоскости. Но наибольший практический интерес представляет дифракция на прост­ранственных (трехмерных) решетках. В качестве пространственных дифракционных решеток могут быть использованы кристаллические тела (например, монокристаллы), так как в них неоднородности (ато­мы, ионы) регулярно повторяются в трех направлениях (рис. 2.10). Этот случай дифракции привел Лауэ (1912 г.) к открытию метода исследования кристаллов при помощи дифракции рентгеновских лучей.

Действительно, для того, чтобы решетка могла эффективно разложить излучение в спектр, её постоянная d должна быть по порядку ве­личины примерно такой же, как и длина волны λ. Для оптической области излучения  это решетка c периодом d  10^-6 м. В природе существуют естественные пространственные структуры с периодом  10^-10 м. Это кристаллы, у которых атомы, ионы или молекулы расположены упорядоченно и образуют пространст­венную периодическую структуру, напоминающую дифракционную решетку. Период кристаллической решетки соизмерим с длинами волн рентгеновской области спектра. Просвечивая кристаллы рентгеновскими лучами, можно определить период кри­стал­лической решетки с по­мощью явления дифракции на пространственной структуре. Таким образом, был разработан структурный анализ кристаллических обра­зова­ний. С другой стороны, ме­тод Лауэ дал возможность определять длину волны рентгеновских лучей, если известна кристаллическая структура той решетки, которая слу­жит дифракционной. Метод явился основой спе­ктроскопии рентгеновских лучей, позволяющей установить важнейшие особенности строения атома.

В 1913 году русский физик Г.В. Вульф и англичанин У.Л. Брэгг предложили простой метод расчета дифракции рентгеновских лучей в кристаллах. Направления, в которых получаются дифракционные максимумы, определяются условием:

, (2.13)

где d – период структуры,  – угол скольжения падающих лучей.

Метод позволяет исследовать спект­ральный состав рентгеновско­го излучения, если известны расстоя­ния между отражающими плоскостями ААиВВкристалла (рентгеновская спектроскопия). И, наоборот, изучать структуру кристаллов (определять расстояние между плоскостями, тип кристаллической решетки и т.д.), если известна длина волны монохроматического рентгеновского излучения (рентгеноструктурный анализ).

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. В чем заключается явление дифракции света?

2. При каких условиях наблюдается дифракция света?

3. Сущность принципа Гюйгенса - Френеля.

4. Сущность метода зон Френеля. Что такое зона Френеля?

5. Как c помощью метода зон Френеля объясняется прямолинейное распространение света?

6. При каких условиях возникает дифракция Френеля?

7. При каких условиях возникает дифракция Фраунгофера?

8. Условия образования максимумов и минимумов при дифракции от одной щели. Что означает величина k в формулах максимумов и минимумов дифракции?

9. Изобразите графически распределение интенсивности света на экране при дифракции на одной щели. Дайте пояснения.

10. Какой вид имеют дифракционные максимумы при освещении щели: а) монохроматическим светом, б) белым светом? Дайте пояснения.

11. Какое устройство называется дифракционной решеткой?

12. Перечислите характеристики дифракционной решетки.

13. Что называют периодом (постоянной) дифракционной решетки? Как вычислить период дифракционной решетки, зная число штрихов на единицу длины?

14. Какую величину называют угловой дисперсией дифракционной решетки? Как увеличить угловую дисперсию дифракционной решетки?

15. Какую величину называют разрешающей силой (разрешающей способностью) дифракционной решетки? Как увеличить разрешающую способность дифракционной решетки?

16. Напишите условия образования главных максимумов и главных минимумов при дифракции на дифракционной решетке.

17. В чем преимущества дифракционной решетки перед щелью?

18. От каких параметров зависит яркость и ширина дифракционного максимума при дифракции на решетке? От чего зависит общее число дифракционных максимумов, полученных на экране за решеткой?

19. Сущность спектрального анализа. Какие характеристики определяются с его помощью?

20.Где применяется явление дифракции рентгеновских лучей? Какие физические характеристики определяются с помощью этого явления?