Оглавление

1.Термодинамические характеристики рабочего тела, параметры состояния. Первый и второй законы термодинамики. Изменение энтропии. 4

2.Кризис течения в сжимаемых жидкостях, запирание по расходу (см. также вопрос 11). 9

3.Вязкость и внутреннее трение в жидкостях и газах. Зависимость вязкости от параметров состояния. 11

4.Законы переноса. Виды и основные понятия пограничного слоя, условные толщины. Понятие о режимах течения и турбулентной вязкости. 12

5.Механизмы перехода кинетической энергии в потенциальную энергию. Параметры торможения. Распределение параметров состояния по обводам обтекаемого тела. 14

6.Основные гидродинамические понятия, свойства элементарной струйки тока, виды расхода, плотность тока. Причины различия расхода через поперечное и живое сечения канала. 16

7.Характерные скорости потока. Эквивалентность изменения скорости и работы расширения-сжатия. Безразмерные скорости и связь между характерными скоростями в размерном и безразмерном виде. 18

8.Газодинамические функции параметров торможения. Критические и полные параметры. 20

9.Нестационарное одномерное уравнение неразрывности в полных и в статических параметрах. Примеры проявления нестационарности (гидроудар, помпаж и пр.). 22

10.Газодинамическая форма уравнения неразрывности. Газодинамические функции расхода. 23

11.Анализ формулы расхода. Запирание каналов по расходу (см. также уравнение Гюгонио). Воздействия, способные вызвать запирание каналов по расходу. 24

12.Частные случаи уравнения Эйлера: радиальное равновесие, универсальный закон изменения окружной составляющей скорости. 26

13.Уравнение движения в форме Громеки–Лемба и интеграл Коши–Лагранжа. Энергетическая форма Крокко. Условия постоянства полной энтальпии. 28

14.Интеграл Бернулли, условия постоянства полной механической энергии. Анализ уравнения Бернулли. 29

15.Уравнение количеств движения (первое уравнение Эйлера) в общем виде. Тензор импульса и его компоненты. Неконсервативная форма для расчета силового взаимодействия потока и обтекаемых тел. 30

16.Методика применения уравнения первого Эйлера, примеры расчета сил (реактивная тяга, силы в решетке профилей). 31

17.Уравнение моментов количеств движения (второе уравнение Эйлера). Крутящий момент, мощность и работа одной ступени лопаточной машины; связь работы с силами, действующими на лопатки. 32

18.Понятие о принципе работы турбомашин. Энергетическая форма уравнения моментов количества движения, коэффициенты нагрузки (закрутки, напора), напорность ступени. 33

19.Общая форма одномерного стационарного уравнения энергии в тепловой и механической форме (обобщенное уравнение Бернулли). 34

20.Уравнение энергии для идеального и реального энергоизолированного течения, политропический интеграл, T-S – диаграммы процессов ускорения/торможения. 35

21.Анализ формулы работы, примеры управления работой расширения/сжатия, КПД процессов расширения/сжатия. Коэффициент теплового сопротивления, коэффициент возврата тепла. 36

22.Изоэнтропный и адиабатный потоки. Работа и КПД турбомашин, T-S диаграммы. 38

23.Характеристики потерь и их взаимосвязь. Особенности гидродинамической трактовки коэффициента потерь кинетической энергии. 41

24.Потери энергии в канале постоянного сечения (трубе) для капельных и сжимаемых жидкостей. Основные виды местных сопротивлений – конфузор и внезапное сжатие, диффузор и внезапное расширение. 43

25.Потери при повороте потока, вторичные течения. Параметры поворота, определяющие величину составляющих потерь при повороте. 44

26.Переход ламинарного режима течения в турбулентный, структура турбулентного пограничного слоя и закон распределения скоростей по его толщине, отрыв пограничного слоя. Расчет коэффициента Дарси для ламинарного режима, турбулентного режима с различной степенью проявления шероховатости (неравенства Сабанеева). Характеристика сети. 45

27.Связь сжимаемости со скоростью потока, вывод и анализ. Другие уравнения и формулы, подтверждающие или повторяющие этот анализ. Уравнение Гюгонио и анализ геометрического воздействия. 49

28.Уравнение обращения воздействий. Краткий анализ воздействий, виды дроссселирования течений (виды кризиса течения). Необходимость комплексных воздействий на поток в турбомашинах. 51

29.Тепловое воздействие, его анализ. Тепловой кризис, проявление в основных и форсажных камерах сгорания. 53

30.Кинематика движения жидкой частицы. Виды движения. Вихревое и потенциальное движение, условия незавихренности, потенциал скорости. Основные понятия. Уравнения, описывающие вихревое течение. 56

31.Теоремы Стокса, Гельмгольца, Томсона. Проявления действия теорем и нарушения их условий (свободные тороидальные вихри; тороидальные вихри, порожденные осевыми вихрями; разгонные вихри; вихревые следы, разрывы и пр.). Расчет потенциального вихря. 58

32.Истечение из косого среза, предел расширительной способности косого среза. 59

33.Законы сохранения в теории скачков уплотнения и ударных волн. Природа потерь в нормальных разрывах поля скоростей. 61

34.Кинематическое соотношение для скачков уплотнения и его анализ. Скорость следа за ударной волной. Динамическое соотношение на поверхностях нормального разрыва. Ударная адиабата Гюгонио. Системы скачков уплотнения. 64

35.Расчет угла фронта косых скачков уплотнения. Предельный угол поворота и возникновение отсоединенных криволинейных скачков уплотнения. 65

36.Режимы истечения из сопла Лаваля. Диаграмма режимов истечения. 66

37.Классификация турбомашин по направлению передачи энергии, по преимущественному направлению потока. Преимущества и недостатки различных типов турбомашин. 68

38.Классификация турбомашин по форме меридионального сечения проточной части, преимущества и недостатки различных схем проточной части. 70

39.Классификация турбомашин по нагруженности, классификация компрессоров и ступеней компрессоров по степени повышения полного давления. Количественные значения соответствующих параметров и краткая характеристика указанных видов турбомашин. 73

40.Классификация турбомашин по скорости обтекания профилей (истечения из межлопаточных каналов). Краткая характеристика указанных видов турбомашин. 74

41.Классификация турбомашин по числу валов. Обоснование необходимости применения многовальных турбомашин. 77

42.Основные показатели работы и параметры турбомашин. Требования, предъявляемые к компрессорам и турбинам. 80

43.Основные геометрические параметры проточной части, ограничения и перспективы развития параметров проточных частей. 81

44.Геометрические параметры профиля, краткий анализ и характерные значения. 82

45.Геометрические параметры решетки профилей и лопаток. Краткий анализ. 84

46.Принцип работы ступени турбомашины. Работа на неизогнутых профилях. Режимы принудительного вращения, авторотации, флюгирования. Необходимые элементы ступени турбомашины и преобразование энергии в этих элементах. 85

47.Принцип работы ступени турбомашины. Передняя и задняя критические точки. Развитие циркуляции вектора скорости на аэродинамическом профиле, распределение давлений по профилю, осевые и окружные усилия. Работа окружных сил. 87

48.Активный и реактивный принцип работы ступени турбомашины. Кинематическая степень реактивности. Термодинамическая степень реактивности. 90

49.Распределение параметров потока по длине ступени в активных и реактивных ступенях. 94

50.Основы расчета ступени турбомашин с использованием степени реактивности. Входная и выходная закрутка потока. 98

51.Анализ влияния кинематической степени реактивности на планы скоростей ступени осевого компрессора. 99

52.Анализ влияния кинематической степени реактивности на планы скоростей ступени осевой турбины. 102

53.Атакоустойчивость профиля и решетки профилей компрессоров и турбин. Характеристика компрессора по потерям (КПД). Факторы, определяющие атакоустойчивость. 106

54.Зависимость работы ступени компрессора от расхода воздуха. Характеристика компрессора по напорности (степени повышения полного давления). Основные режимы работы компрессоров и границы области рабочих режимов. 109

55.Особенности характеристик центробежных компрессоров с различной формой лопаток. 113

56.Обобщенные и универсальные характеристики компрессора. Приведение параметров компрессора к стандартным атмосферным условиям. Возможные погрешности формул приведения. 117

57.Газодинамические основы рассогласования работы первых и последних ступеней компрессора (ступени и сети) на нерасчетных режимах работы. 121

58.Помпаж компрессора на малой частоте вращения ротора. Различие в газодинамической устойчивости компрессоров разной напорности. Влияние густоты решеток первых ступеней на запас газодинамической устойчивости. 122

59.Помпаж компрессора на повышенной частоте вращения ротора. Помпаж на переходных режимах, влияние параметров камеры сгорания. Общий принцип влияния на газодинамическую устойчивость параметров других узлов, образующих напорную сеть компрессора. 125

60.Вращающийся срыв в компрессорах, надроторные устройства. 126

61.Изменение расхода воздуха через компрессор по частоте вращения. Регулирование компрессора с помощью перепуска воздуха. 128

62.Регулирование компрессора с помощью поворотных направляющих аппаратов. 131

63.Регулирование компрессора, 2-х и более вальная схема компрессора, изменение скольжения роторов при изменении частоты вращения. 134

64.Короткие, средние и длинные лопатки. Профилирование длинных лопаток по высоте, законы профилирования. Основные положения и уравнения для расчета планов скоростей по высоте. 138

65.Профилирование по закону постоянной циркуляции и закону постоянного угла выхода из соплового аппарата, сравнение с законом постоянной реактивности. 140

66.Профилирование по закону постоянной реактивности (твердого тела), сравнение с законом постоянной циркуляции. 144

67.Общая номенклатура потерь в решетках турбомашин, краткая характеристика видов потерь и их зависимость от основных режимных и геометрических параметров. 145

68.Дополнительные потери в турбомашинах: от нестационарности, в зазорах, на трение о диски, на охлаждение, с выходной скоростью. 148

69.КПД турбомашин: адиабатный по параметрам торможения, адиабатный по статическим параметрам за турбиной/ступенью (мощностной), политропный. 149

70.Зависимость адиабатного и мощностного КПД от отношения U/C1. 150

71.Оптимальные планы скоростей одноступенчатой турбине при переменной степени реактивности. Управление отношением U/C1. 152

72.Распределение работы, КПД, осевой скорости и степени реактивности по ступеням многоступенчатых компрессоров. 155

73.Распределение работы, КПД, осевой скорости и степени реактивности по ступеням многоступенчатых турбин. 158

74.Предел реализуемой в ступени турбины и отдельных лопаточных решетках работы (см. вопросы 28, 32). Влияние предела расширительной способности косого среза и запирания каналов по расходу. 160

75.Многоступенчатые турбины, турбины со ступенями скорости и ступенями давления. 161

76.Параметры нагруженности y, y* для многоступенчатых турбин, параметры напряжений т и Fn2. 162

1. Термодинамические характеристики рабочего тела, параметры состояния. Первый и второй законы термодинамики. Изменение энтропии.

Совершенный газ – упрощенная модель реального газа, с принятыми допущениями:

• Полностью отсутствуют межмолекулярные силы;

• Молекулы в виде материальных точек, обладающих массой;

• Теплоемкость, газовая постоянная, показатель адиабаты и молярная масса неизменны и не зависят от температуры;

• Агрегатное состояние неизменно при любых условиях.

Газ можно рассматривать как совершенный до температуры 2500 К, при более высоких температурах начинаются процессы диссоциации, ионизации и рекомбинации.

Идеальный газ – совершенный газ, лишенный свойств вязкости.

Параметры состояния рабочего тела:

Давление. Согласно МКТ, давление – результат ударов хаотически и непрерывно движущихся молекул о стенки сосуда. Основное уравнение кинетической теории для модели идеального газа:

число молекул вещества в ;масса молекулы, кг;средняя квадратичная скорость молекул, м/с; число Авогадро (число молекул в 1 кмоле); молярная масса вещества, кг/кмоль; молярный объем вещества, .Моль – количество вещества, в котором содержится столько молекул, сколько содержится атомов в изотопе углерода массой 0,012 кг.

При постоянной температуре давление определяется только числом молекул в единице объема, и не зависит от рода молекул. При свойства газа определяются только числом молекул.

Температура. Согласно МКТ, абсолютная термодинамическая температура – величина, пропорциональная средней кинетической энергии поступательного движения молекул газа. По уравнению Больцмана, для модели идеального газа:

константа Больцмана.

Абсолютный ноль температуры – ноль по шкале Кельвина , при котором прекращается движение молекул.

Плотность и удельный объем. Это количество вещества, заключенное в единице объема:

Эти три параметра состояния связаны между собой уравнением Клапейрона-Менделеева, для одного килограмма идеального газа:

удельная газовая постоянная, Дж/кг∙К. При умножении на молярную массу, получаетсяуниверсальная газовая постоянная, одинаковая для всех газов (на основании закона Авогадро о том, что при одинаковых давлении и температуре все газы имеют одинаковый молярный объем, при н.у. равный 22,4 м³/кмоль).

Значение универсальной газовой постоянной при н.у. (101325 Па и 273,15 К) равно:

Вид термодинамического процесса определяется показателем политропы , из уравнения политропного процесса, для идеальных газов:

При процесс будет изобарным,изотермическим,изохорным,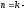адиабатным. Чем выше показатель политропы, тем меньше сжимаемость и больше упругость газов.

Теплоемкость тела – количество тепла, необходимое для нагрева единицы вещества на один градус Кельвина. Истинная теплоемкость соответствует бесконечно малому изменению температуры:

В газодинамике используют массовые теплоемкости – изобарную и изохорную:

показатель адиабаты.

Энтальпия – сумма потенциальной внутренней энергии и потенциальнойэнергии давления для единицы вещества:

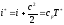
Уравнение состояния через полную энтальпию и внутреннюю энергию :

Модуль упругости – количественная оценка сжимаемости газа, отношение изменения давления к вызванному им относительному изменению плотности:

Упругость газов, в зависимости от давления и вида термодинамического процесса, на 3-4 порядка меньше упругости капельных жидкостей. На малых скоростях газовых потоков их свойство сжимаемости проявляется незначительно, поэтому их рассматривают как поток капельной жидкости.

Первый закон термодинамики: подводимые к газу удельное тепло трения и внешнее теплорасходуются на изменение внутренней энергиии на работу деформации, иначе говоря, на изменение энтальпии и работу проталкивания:

Второй закон термодинамики: рост количества подводимого тепла увеличивает приращение энтропии, в то время как рост температуры, при которой к системе подводится тепло, снижает приращение энтропии.

Свойства реальных рабочих тел описываются уравнением Ван-дер-Ваальса:

экспериментальная константа, характеризующая силы межмолекулярного взаимодействия, суммарный объем, занимаемый молекулами при. Влияние переменных уравнения на давление:

К увеличению давления приводит:

увеличение скорости хаотического движения молекул;

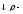
увеличение концентрации молекул увеличивает межмолекулярные силы;

уменьшается оттягивающее действие на молекулы, приближающиеся к стенке;

уменьшение свободного пробега молекул и увеличение количества ударов о стенку;

Также уравнение состояния может иметь вид , гдекоэффициент сжимаемости природного газа, определяется по номограммам.

2. Кризис течения в сжимаемых жидкостях, запирание по расходу (см. также вопрос 11).

Кризис течения.

Расширение сплошной среды при ускорении и противодействующий ему нарастающий уровень межмолекулярных сил рано или поздно приходят к критическому состоянию, когда межмолекулярные силы притяжения при ускорении среды не способны удержать среду от резкого, катастрофического расширения.

Кризис течения – одно из свойств сплошных сред. В газах и капельных жидкостях он разрешается различным способом.

В газах при вызванном ускорением расширении статическое давление снижается по отношению к давлению торможения до критической величины, однозначно связанной с полным давлением. Эта связь зависит лишь от рода газа, определяемого показателем адиабаты k:

При достижении критического давления расстояние между молекулами также становится критическим, а критическая скорость потока сравнивается с местной скоростью звука в данном сечении. При дальнейшем, сверхкритическом увеличении расстояния между молекулами закон их взаимодействия меняется: межмолекулярные силы начинают убывать обратно пропорционально квадрату расстояния. Данное явление приводит к тому, что эти силы оказываются не в состоянии противодействовать стремлению газа расширяться как в продольном, так и в поперечном к течению направлении. В связи с этим сверхкритическое ускорение газовых потоков требует, в отличие от докритических режимов или ускорения жидкостей, уже расширяющегося канала.

Запирание канала по расходу.

Если скорость дозвукового (докритического) потока плавно увеличивать на входе в канал постоянного сеченияпри неизменных прочих условиях, то ГДФувеличивается, достигая максимального значения, равного единице, при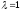(кризис течения).

–газодинамическая формула расхода.

Тогда расход также принимает максимальное значение:

, где площадь является минимальной для данного канала и в силу достижения потоком звуковой скорости течения получает название критической площади:. Достигнутая потоком звуковая скорость течения в случае всасывающего канала является максимально возможной:.Дальнейший ее рост невозможен, т.к. при переходе к сверхзвуковым скоростям ускорение потока осуществляется в расширяющихся каналах. В этом случае принято говорить, что канал или течениезапирается (закрывается) по расходу.

Увеличение площади поперечного сечения F сопровождается снижением , а значит, и ростом скорости сверхзвукового потока, который может ускоряться при постоянном массовом расходедо максимальной скорости.

3. Вязкость и внутреннее трение в жидкостях и газах. Зависимость вязкости от параметров состояния.

Вязкость – свойство сплошных сред оказывать сопротивлению сдвигу двух слоев относительно друг друга. Сдвиг должен сопровождаться только изменением формы, но не объема.

Для твердых тел справедлив закон Гука, устанавливающий пропорциональную связь сдвиговых деформаций и касательных напряжений.

,

где τ – касательное напряжение сдвига;

R_τ – усилие сдвига;

F – площадь обтекания, на которую действует сила трения;

G – модуль упругости второго рода;

dγ – угловая деформация при сдвиге.

Связь с поперечным градиентом скорости опытным путем установил Ньютон в форме закона о молекулярном трении в жидкостях и газах:

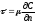
где μ – коэффициент пропорциональности, называемый динамическим коэффициентом вязкости; n – нормаль к обтекаемой поверхности.

Зависимость напряжений трения от скорости деформации для легкоподвижных сред:

Скорость деформации может по-разному влиять на поведение обладающих высокой вязкостью жидкостей или твердых аморфных тел. Так, стекло, смолы, битум при высокой ударной скорости деформации могут испытывать хрупкое разрушение, но текут при длительном медленном силовом воздействии. Аналогично могут вести себя и капельные жидкости.

Молекулярно-кинетическая природа вязкости

Трение в капельных жидкостях заключается, главным образом, в преодолении сил взаимодействия между молекулами слоев, смещаю­щихся относительно друг друга. С увеличением температуры капель­ной жидкости увеличиваются ча­стота колебаний молекул и силы взаимодействия между ними умень­шаются, а вместе с ними уменьша­ется и вязкость. Величина для капельных жидкостей определяется экспериментальным путем.

Трение в газах обусловлено пе­реносом направленного количества движения молекул при их тепловом хаотическом движении. Пусть два соседних слоя газа движутся в од­ну сторону с различными скоростя­ми («быстрый» и «медленный» слои). Молекулы «быстрого» слоя, переходя в «медленный», уско­ряют его молекулы, а сами подтормаживаются и наоборот. С уве­личением температуры газа скорость хаотического движения мо­лекул и число соударений возрастают, а вместе с этим — перенос количества движения и вязкость газа.

4. Законы переноса. Виды и основные понятия пограничного слоя, условные толщины. Понятие о режимах течения и турбулентной вязкости.

В реальных газах в силу их теплопроводности поперечный перенос тепла появляется при неравномерном распределении термодинамических параметров. Перенос тепла вдоль вектора скорости обычно возникает не вследствие теплопроводности, а за счет излучения (при достаточно большой разнице температур).

Поперечный перенос тепла описывается законом Фурье:

,

где q – секундное количество тепла;

λ – коэффициент теплопроводности.

Теплопроводность определяется, как и вязкость, молекулярно-кинетическими процессами и тоже зависит от температуры.

Секундный перенос вещества через единицу поверхности по нормали к ней описывается законом Фика:

,

где D – коэффициент диффузии;

с – концентрация вещества в потоке.

В соответствии с тремя процессами поперечного переноса в газах различают три вида пограничных слоев:

1. Тепловой пограничный слой при достаточно большой скорости потока когда температура торможения и, соответственно, температура обтекаемой поверхности начинают существенно отличаться от статической температуры в потоке. Возникает при нагреве или охлаждении поверхности извне потока.

2. Диффузионный пограничный слой может возникать при парении так называемых амляционных (уносимых или испаряемых) покрытий. Их применяют для защиты поверхностей от высоких температур. Примером могут служить наружные поверхности возвращаемых космических аппаратов. Одновременно возникает и тепловой пограничный слой.

3. Гидравлический пограничный слой зависит от числа Рейнольдса и может быть ламинарным и турбулентным. Толщина динамического пограничного слоя определяется как то расстояние от поверхности тела (или от границы раздела жидкостей), на котором скорость в пограничном слое можно практически считать равной скорости во внешнем потоке.

Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости как правило наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, при этом наибольшей скоростью обладает слой, который движется вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоростей, которые перпендикулярны течению, и они могут двигаться из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется незначительно. Так как частицы жидкости могут перейти из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Профиль усредненной скорости при турбулентном течении в трубах (рис. 2) отличается от параболического профиля при ламинарном течении в трубах более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения.

Турбулентная вязкость

Вязкость, обусловленная турбулентным характером движения жидкости или газа, т. е. обменом количествами движения между слоями жидкости или газа. Турбулентная вязкость преобладает над малозначительной молекулярной вязкостью. Турбулентная вязкость характеризует не физические свойства жидкости, а статистические свойства пульсационного движения. Поэтому она не является постоянной величиной, а может изменяться как в пространстве, так и во времени.

5. Механизмы перехода кинетической энергии в потенциальную энергию. Параметры торможения. Распределение параметров состояния по обводам обтекаемого тела.

1. Диссипация

Пограничный слой на стенке является двумерным, поскольку скорость потока меняется и по нормали к поверхности, и вдоль поверхности. Поток вне пограничного слоя, называемый основным (невозмущенным) или ядром потока, практически одномерен, т.к. скорость среды может меняться только в узком слое вдоль потока под влиянием трения у поверхности. Приходящийся на единицу массы секундные составляющие работы вязкостных сил для двумерного потока будут равны:

Составляющая скорости , вызванная выделением тепла трения, в силу ее малости, а также производные от нее, опущены. Непосредственно на поверхности скорость равна нулю. Следовательно работа по переносу количества движения на стенке равна нулю и вся работа сил вязкости полностью является работой тепловыделения

Итак, на обтекаемой стенке в сплошных течениях всегда имеет место полная диссипация кинетической энергии. Она приводит к повышению по мере приближения к стенке только внутренней энергии газа, потенциальная энергия давленияостается неизменной. Диссипативный процесс необратим, поэтому израсходованная на тепло кинтеическая энергия не может восстановиться в виде механической, какой является энергия давления. В продольном по отношению к обтекаемой поверхности направлении диссипация в силу своей необратимости приводит к уменьшению потенциальной энергии давления, т.к. эта энергия расходуется на восполнение потерь кинетической энергии вдоль пограничного слоя. Статическое давление и плотность вдоль пограничного слоя уменьшаются. Это справедливо только для прямолинейных каналов постоянного поперечного сечения с дозвуковым потоком.

2. Изоэнтропное торможение

В изоэнтропном процессе торможения потерь механической энергии нет, соответственно давление и плотность торможения остаются вдоль канала постоянными.

3. Политропное торможение (диссипация + изоэнтропное торможение)

Сопровождается потерями механической энергии, давления и плотности торможения (меньшими, чем при полной диссипации).

Для получения истинного значения полных энтальпии и температуры достаточен энергоизолированный процесс. Внутренние тепловые преобразования не оказывают влияния на суммарную энергию потока в ее тепловом эквиваленте.

статические и полные параметры можно связать по идеальной адиабате:

Сами полные параметры могут быть определены по формулам:

При постоянной плотности давление торможения находится проще:

6. Основные гидродинамические понятия, свойства элементарной струйки тока, виды расхода, плотность тока. Причины различия расхода через поперечное и живое сечения канала.

Стационарное течение – установившееся движение потока, параметры которого зависят только от координат точки.

Нестационарное течение – неустановившееся течение, параметры которого зависят от координат точки и от времени.

Течения могут быть трех-, ­двух- и одномерными, параметры в которых меняются соответственно вдоль трех, двух или одной координаты. Плоское­ (двумерное) и одномерное сечения используют для приближенных расчетов.

Векторная линия – такая линия в векторном поле, каждой точке которой в данный момент времени может быть поставлен в соответствие вектор, направленный по касательной к данной линии.

Линия тока – векторная линия в поле линейных скоростей. Показывает мгновенное направление движения жидкости вдоль некоторой кривой. В установившемся движении геометрически совпадает с траекторией. Уравнение линии тока:

Вихревая линия – векторная линия в поле угловых скоростей вращения частиц относительно собственных осей. Можно представить как мгновенную криволинейную ось вращения совокупности частиц.Понятие справедливо только в вихревом движении. Уравнение вихревой линии тока:

Траектория – графическое изображение пути, пройденного конкретной частицей за определенный промежуток времени.

Трубка тока – поверхность, образованная множеством линий, проведенных через бесконечно малый замкнутый контур, плоскость которого не совпадает с направлением соответствующей векторной линии.

Элементарная струйка тока – трубка тока, заполненная жидкостью (множеством линий тока). Распределение параметров по сечению трубки считают равномерным, т.е. сечение принимается одномерным.

Вихревой шнур – вихревая трубка, заполненная жидкостью. Понятие справедливо только в вихревом движении.

Поток – совокупность элементарных струек тока.

Вихревое течение – совокупность вихревых шнуров. Понятие справедливо только в вихревом движении.

Винтовое движение – совпадение вихревых линий и линий тока.

Потенциальное движение – движение, в котором отсутствует вращательное движение частиц среды относительно собственных осей. В каждой точке выполняется равенство .

Вихревое движение – движение, в котором ротор или циркуляция скорости по любому замкнутому контуру отличны от нуля (происходит вращение частиц).

Ламинарное движение – слоистое и упорядоченное течение, в котором интенсивность вихревого движения и силы инерции недостаточны для развития макровихрей, когда во вращение вовлечены целые группы молекул и частиц. Подобно вихревому течению.

Турбулентное течение – течение, слои в котором интенсивно перемешиваются из-за возникновения макровихрей, участвующих в поперечном переносе количества движения. Поле скоростей по сечению выравнивается, что на микроуровне приводит к снижению интенсивности вихревого движения. Ассоциируется с потенциальным движением.

Расход – количество вещества, протекающее в единицу времени через площадь поперечного сечения канала. Различают массовый (кг/с) и объемный (м³/с) расходы.

Плотность тока – расход, отнесенный к единице площади сечения. Векторная величина, так как определяется скоростью течения. Различают массовую ()иобъемную (скорость потока ) плотность.

угол между вектором внешней нормали к поверхностии вектором скорости.

Поперечное сечение – сечение, для которого ось канала является нормалью.

Живое сечение – такое сечение площадью , каждая элементарная площадка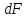которого нормальна соответствующему вектору скорости. Расход через живое сечение вычисляется интегрированием по, уголпри этом не учитывается. Расход черезбольше фактического расхода (через площадь поперечного сечения), так как включает радиальную составляющую скорости течения, не участвующую в продольном переносе массы. Применяется для визуализации течений и показа структуры течения.

7. Характерные скорости потока. Эквивалентность изменения скорости и работы расширения-сжатия. Безразмерные скорости и связь между характерными скоростями в размерном и безразмерном виде.

Местная скорость звука

Скорость распространения слабых возмущений в упругой среде. ;.

С ростом статической температуры местная скорость звука увеличивается. Это объясняется молекулярно-кинетической природой распространения звуковых волн. При увеличении температуры скорость хаотического движения частиц увеличивается, они быстрее преодолевают расстояние, равное длине свободного пробега молекул и быстрее передают возмущение.таким образом, распространение слабых возмущений представляет собой продольную волну.

Местная скорость звука зависит от рода газа, с ростом газовой постоянной местная скорость звука увеличивается, что объясняется ростом скорости хаотического движения молекул, связанной с уменьшением молярной массы.

Скорость потока

Полученная формула показывает, что скорость потока определяется расходуемым на кинетическую энергию теплоперепадом.

Выносим полную температуру за скобку, С учетом изоэнтропичности связи полных и статических параметров отношение температур заменяется отношением давлений, и в результате получим общепринятую формулу скорости потока:

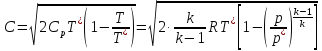
Равенство показывает зависимость скорости потока не только от начального запаса энергии, но и от степени преобразования потенциальной энергии в кинетическую, оцениваемой величиной или. Перепад температур не является определяющим для возникновения течения, он лишь связан с первопричиной изменения скорости потока – перепадом давлений или плотностей, задающим величину и направление силового воздействия на поток.

Скорость потока, как и местная скорость звука и любая иная скорость, зависит от рода газа. Легкие газы в одинаковых условиях развивают большую скорость, чем тяжелые, поскольку у них выше газовая постоянная.

Кроме того, на величину скорости потока влияет сжимаемость среды. Если принять среду несжимаемой, то:

Где . Формула дает более высокое значение скорости, что обусловлено снижением статической плотности при ускорении сжимаемой среды.

Максимальная скорость

Достигается тогда, когда вся потенциальная энергия полностью и без потерь переходит в кинетическую. Максимальная скорость – скорость истечения в пустоту, где .Является теоретическим пределом и реально никогда не достижима, даже при фактическом истечении в вакуум (ракета). Т.к. при ускорении газа происходит его расширение и охлаждение, то задолго до достижения предельной скорости либо произойдет потеря сплошности, либо газ сконденсируется (пример: углекислотный огнетушитель, резкий выброс влажного воздуха из емкости высокого давления – газ конденсируется и становится видимым, индуктивные вихри на концах крыла самолета).

Критическая скорость

Такая скорость, при которой скорость потока и местная скорость звука в данном сечении одинаковы.

Критическая скорость звука зависит только от рода газа и полной температуры.