Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

итог3

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

246.7 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

фика.

y =

- x2

1. Функция определена и непрерывна на всей оси OX за исключением

точек x1 = -

3; x2 = 3 .

2. Определим односторонние пределы в точках разрыва:

lim

= ¥,

lim

= -¥, lim

= ¥,

3 - x2

- x2

x→−

−0

x→−

x→+

−0 3

lim

= -¥.

3 - x2

x→+

Значит, точки x = ±

есть точки бесконечного разрыва.

3. Функция нечетная, т.к. y(-x) =

= -y(x)..

3 - x2

Ее график симметричен относительно начала координат.

4. При x = 0 y = 0 , т.е. график функции проходит через начало коорди- нат. Интервалы оси OX , в которых функция сохраняет постоянный знак:

(-¥;-3) - здесь y > 0 ; (-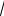3;0) - здесь y < 0.

В силу симметрии графика функции:

(0; 3) - здесь y > 0 ; (3;¥) - здесь y < 0.

5. Прямые x = -3 и x = 3 есть вертикальные асимптоты графика.

В соответствии с результатами п.2 при x ® -3 слева функция неограни- ченно возрастает, а при стремлении справа неограниченно убывает. Анало-

гично поведение функции вблизи точки x = 3.

Определим невертикальные асимптоты

	x	3			æ	x	3		ö
	x				ç	x			÷
k = lim			2		ç			2	÷	= 0.
k = lim	- x		2	)x	= -1;b = limç	3- x		2	+ x÷	= 0.
x→∞ (3	- x			)x	x→∞è	3- x			ø

Те же значения коэффициентов при x → −∞ . Заключаем, что график исследуемой функции имеет невертикальную асимптоту y = −x .

6. Найдем интервалы возрастания и убывания функции и точки экс- тремума:

ö′

(3- x

) + x

×2x

- x

)

y'= ç

3- x

(3- x

)

Приравняем числитель выражения к нулю в найдем критические точки: x2 (9 - x2 ) = 0, x1 = -3, x2 = 0, x3 = 3.

Производная может менять знак при переходе аргумента через эти точки

и точки разрыва x = ±

3. Составим таблицу:

(−∞;−3)

−

(

−

(

−

(0;

(

(3;+∞)

3;0)

3;3)

−

∞

убывает

миним.

возрас-

т.разр

возрас-

нет

возрас-

т.разр

возрас-

макс.

убы-

тает

экстр

тает

вает

Таким образом, при

x = −3 функция имеет минимум,

а при x = 3 -

максимум.

Определим

ординаты

точек

экстремума:

y(−3) = 4,5;

y(3) = −4,5.

7. Найти интервалы выпуклости и вогнутости графика функции и

точки перегиба:

æ x2 (9 - x2 ) ö′

6x(4x2

+ 9)

y"= èç

(3 - x2 )2 ø÷

= (3 - x2 )3 .

Видно,

что

y′′ = 0

только при x = 0 . Вторая производная может ме-

нять знак только в этой точке и точках разрыва. Составим таблицу:

(-¥;

− 3

(0;

(

3;0)

3;¥)

∞

вогнута

т.разрыва

выпукла

т.перегиба

вогнута

т.разрыва

выпукла

Значит, x = 0 - абсцисса точки перегиба.

8. Все результаты исследования используем для построения графика.

-3 − 3

+ 3 +3

Рис. 3.1.

Вычерчивание графика следует начинать с нанесения на плоскость его асимптот, затем точек экстремума и перегиба данной функции. Знание интер- валов возрастания и убывания функции, выпуклости и вогнутости, а также

поведение функции вблизи асимптот помогут вычертить график осмысленно и точно.

Наибольшее и наименьшее значения функции на отрезке

Нахождение наибольшего и наименьшего значений непрерывных функ- ций основывается на следующих свойствах этих функций:

если в некотором интервале (конечном или бесконечном) функция f (x)

непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале; если функция f (x) непрерывна на некотором отрезке [a,b], то она

обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.

Таким образом, для нахождения наибольшего и наименьшего значений функции f (x) на отрезке [a,b] следует:

1.Найти критические точки, лежащие внутри отрезка [a,b] и вычислить значения функции в этих точках.

2.Вычислить значения функции на концах отрезка, т.е. f (a) и f (b) .

3.Из всех полученных значений функции выбрать наибольшее и наи- меньшее.

Пример.	Найти наибольшее	и наименьшее значения функции
y = x − 2ln x на отрезке [1, e] .
Решение:		функции y'= (x − 2ln x)′ =1− 2
1. Найдем	критические точки	функции y'= (x − 2ln x)′ =1− 2	x	,
			x

y'= 0 при	x = 2, y(2) = 2(1− ln 2). Других критических точек внутри дан-
ного отрезка нет.
2.	Вычислим	значения	функции	на	концах	отрезка:
y(1) =1, y(e) = e − 2.

3. Сравним полученные значения: y(1) > y(e) > y(2).

Таким образом, наибольшее значение функции y(1) =1, а наименьшее – y(2) = 2(1− ln 2).

Контрольная работа №3 по теме

«ВВЕДЕНИЕ В АНАЛИЗ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

ОДНОЙ ПЕРЕМЕННОЙ»

3.1 Найти пределы:

1- 2x -3x2

3.1.1а) lim

;

б) lim

1+ x

1- x

;

+10x -

x→∞ 5x2

x→0

1- cos x

2x + 3 ö

в) lim

;

г) limç

;

5x2

x→0

x→∞è

2x - 2 ø

д) lim

2x6 + 3x5 -5

;

е) lim

x5 + x

+ x3 + x - 3

x→1

x→∞

3x6 -1

+ 5x2 + 7x +11

-3

3.1.2 а) lim

;

б) lim

2 + x

;

x - 7

x→∞ 2x3 - 5x2 - 7x -11

x→7

в) lim

x→0

д) lim

x→∞

3.1.3 а) lim

x→∞

arcsin 3x	;		г)

5x
3x6 - x5 - x4 + x2 + x + 2			; е)
4x5 +100

3x4 + 4x2 + 5x - 6		;	б)
π 2 - 2x4


æ		2x -1ö				2x
limç				÷			;
limç				÷			;
x→∞è		2x +1ø
lim	x5 + 2x4					+ x2 - 3x -10		.
lim	x4 + 2x3				+		3x2 + 5x - 2	.
x→−2	x4 + 2x3				+		3x2 + 5x - 2
lim			x				;
lim							;
x→0		1-3x -1

5 x

в) lim

;

г) lim(1+ 2x)

;

arctg

x→0

x4 + x

2 + x - 3

x4 + x2 + x

д) lim

;

е) lim

2x4 + 3x -5

5(x3 + x2 - x -1)

x→1

x→∞

5x2

+ 3x +1

3.1.4 а) lim

;

б) lim

2x -1

;

x -3

x→∞ 3x2 +

2x +

x→3

æ x

в) lim

è 2

;

3x2

x→0

д) lim

3x100 +1

;

x→∞ 4x99 +

3.1.5

а) lim

5x4 + x + 3

;

x→∞ x4 -12x +1

в) lim

x2ctg2x

;

sin 3x

x→0

д) lim

x3 -3x2 + 2x - 6

;

x2 + 2x -15

x→3

3.1.6

а) lim

2x2 + 6x - 5

;

5x2 - x - 0.1

x→∞

в) lim

cos x - cos3 x

;

x→0

д) lim

x4 + x3 + x2 + x - 4

;

x3 +

2x2 + 2x -

x→1

3.1.7

а) lim

x - 2x2 + 5x4

;

2 + 3x2 + x4

x→∞

в) lim

1− cos6x

;

x→0

1- cos2x

д) lim

5x4 + 5x3 + x

2 -11

;

x3 + x2 -

x→1

3.1.8

а) lim

8x5 -3x2 + 9

;

2x5 +

2x2 + 5

x→∞

в) lim(5x ×ctg3x);

x→0

x -1

ö 5x

г)

lim

2x +

x→∞è

е)

lim

2x4 + x2 - 3

x→−1 3x6 + 2x4 - x2 -

б) lim

1+ 3x

1- 2x

;

x + x2

x→0

г)

lim (2x(ln(x +1) - ln x));

x→+∞

е)

lim

7x7 - 0.3x

x→+∞ 4x8 + 0.2x2

б) lim

1- 1- x2

;

x→0

æ x

г)

lim

(ln(x

-1) - ln x)÷;

x→∞è

е)

lim

x4 + x2 +1

x→−∞ 10x3 +11x +12

б) lim

1+ 3x2 -1

;

x2 + x3

x→0

г) lim ((x - 5)(ln(x - 3) - ln x));
x→+∞
е) lim	1- x - x2 - x3 - x4							.
е) lim					2 - x5			.
x→−∞					2 - x5
б) lim				x - 2			;
б) lim							;
x→2				2x -	2
г) lim		x2 - 4				;
г) lim						;
x→2			2x - 2

д) lim

5x4 + 5x3 + x

2 -11

;

x3 + x2 -

x→1

3.1.9

а) lim

2x3 + x2 - 5

;

x3 + x - 2

→∞

в) lim

1- cos 2x

;

0.1

x→0

д) lim

x4 -18x2 +81

;

2x2 -3x - 9

x→3

3.1.10

а)

lim

7x4 - 2x3 + 2

;

x4 + 3

x→∞

в)

lim

1− cos4x

;

2x × tg2x

x→0

д)

lim

11x2 + 9x - 20

;

x5 - x4 - x3 +

2x2 - x

x→1

3.2. Найти производные

+ 3

y = 4x4 -53 x2

3.2.1.

а)

в) y = cos x /(sin x − 2) ;

д)

1+cos

2 x

;

y = 3

ж)

y = ctgln2 x ;

3.2.2.а) y = 3x5 + 21x3 + x3 + 5 ;

в) y = cos x × x ;

д) y = arctg x -1 2 ;

ж) y = lg(4x - x2 ) ;

е)

lim

- x5 + 2x4 -1

2x4 -

3x -

x→+∞

x -

б) lim

;

x2 - x

x→1

lim

4x +1ö2x

;

г)

x→∞è

е) lim

0.1x5 + 0.2x

4 + 0.3

0.1x6 + 0.2x

x→∞

б)

lim

1+ 3x

2x + 6

;

x2 -5x

x→5

2x - 5 öx−1

г)

lim

;

2x +1

x→∞è

е) lim

1- x8

- x7

x→∞

б)

y = ctgx ×2x ;

г)

y =15ln(2x +1) ;

е)

y = arcctg

x + 2

;

3- x

б)

y =

sin x

;

x -3

г)

y = 3sin x ;

е)

y = sin 2

;

1- x2

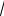3.2.3.а) y = 5x7 - 32x - x42 + 51 ;

в) y = ctglg x ;

д)

y =

arccos x2

;

arcctg 1

ж)

y = log5 (1- x2 ) ;

3.2.4. а)

y =

+13;

y = cos2x ×arcsin

;

в)

д)

y = arctg

x2 - 4 ;

ж)

y = ctg(2x + 3x2 ) ;

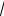3.2.5.а) y = 4x3 - 25x + 1x + 7 ;

в) y = arccos x2 ;

tg 2x

д) y = cos2 2x ;

ж) y = 3 xx +-11 ;

3.2.6.а) y = 7x - 23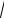x2 + 3x -12 ;

в)	y =	sin x2	;
в)	y =	ctgx	;
		ctgx
д) y = e− x2 +2x ;
ж)	y = 3cos2			1	;
ж)	y = 3cos2		1+ x2		;
			1+ x2

б) y = arcsin 2x 2-1 ;

г) y = x3 ×10x ;

1 + 2

е) y = ex x2 ;

б)	y = cos2x + 3sin x ;
г)	y = tg		ex	;
г)	y = tg		x2	;
			x2
е)	y = ln(x2 + 3					x	) ;
б)	y = cos x ×arcsin x ;
г)	y =	ex - e−x			;
г)	y =		2x		;
			2x

е) y = log7 (1- x3 ) ;

б) y = lg x + cos 2x ;

г) y = arcsin( x2 × x -1) ;

е) y = (1+ ln cos)2 ;

y = 51× x7 -

;

3.2.7. а)

cos2x

в)

y =

;

sin x2

д)

10x+3x2

;

y = 2

y = 2sin

ж)

÷ ;

+ x ø

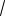3.2.8.а) y = x10 + 3x - 1x + 32 ;

в) y = sin x ×arcsin x ;

	æ		x	ö
д)	ç	2	x+1 ÷		;
д)	y = tgç	2		÷	;
	è			ø
ж)	y = arctgln(1-3x) ;

3.2.9.а) y = 8x3 - 44x3 - x23 + 3;

в) y = ln arcsin x ; arcsin ln x

д) y = 3 1- x2 ;

1+ x2

ж) y = 3x ×arcctgx + xx+-12 ;

3.2.10.а) y = 7× x8 - 4x5 + x54 - 7 ;

в) y = cos3 e x ;

= lg(x2 -1) д) y ln(1- x) ;

ж) y = ctgln(2x + x2 ) ;

б)

y = lg x - arcsin

;

г)

y = arccos(2x ×

1- x2 ) ;

е)

y = (1+ cosln x)3 ;

б)

y = ecos x ;

г)

y =

cos x

;

е)

y = log3 (x2 - x + 2) ;

б) y = x4 ×e

;

г)

y = ctg2x ;

е)

y =

;

sin 3(x−1)

б) y = (1+

)2 ;

1+ x

г)

y = sin 2x ×arcsin 3x ;

е)

y =

;

arccos7x

x+1 ;

				91
3.3. Найти производную
3.3.1.	y2 -	x	=1;	3.3.2. xy -sin( y × x) = 0 ;
3.3.1.	y2 -	y	=1;	3.3.2. xy -sin( y × x) = 0 ;
		y

3.3.3.y = cos xy - y2 ;

3.3.4.arcsin( x × y) + cos(x × y) =1;

3.3.5.y = 3x- y + lg(x + y) ;

3.3.7. tg(x - y) + y ×ctgx = 0 ; 3.3.9. 7x × y + cos(x - y) =1;

3.4. Найти производную

3.4.1. y = xx2 ;

3.4.3. y = (ln x)x ; 3.4.5. y = (x -1)x2 ; 3.4.7. y = (lg x) 3.4.9. y = (x -1)(x+1) ;

3.5. Найти производную

ìx = cost - t sin t
3.5.1. í				;
îy = t2 -sin 3t
ìx = 5t ln t				;
3.5.3. í				;
îy = (3t2		+	4)4
ì	arctgt
ïx =
ïx =	t2		;
3.5.5. í	t2		;
ï		-1)
îy = ln(t		-1)

3.3.6.

10×

+ ctg(x + y) = 3 ;

3.3.8.

ex×y + 8

=10x ;

x - y

3.3.10.

2y-x + lnç

= 0 ;

3.4.2.

y = (cos x)sin x ;

y = (

)x ;

3.4.4.

1- x

3.4.6.

y = (tgx)arcsin x ;

3.4.8.

y = (2x)2x ;

3.4.10. y = (sin x)cos 2x ;

ïx =

-1)

3.5.2.

;

îy = e

ìx = t ×cost

3.5.4.

;

ïy =

sin t

ïx = ln(1-

)

3.5.6.

;

(t +1)

îy =

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.03.201514.84 Кб46История.docx
#
29.03.201528.63 Кб11Исходные данные для проведения АХД.docx
#
01.03.2025613.38 Кб0Исходные данныеАД.doc
#
29.03.20152.24 Mб126итог1.doc
#
29.03.20151.07 Mб35итог2.doc
#
29.03.2015246.7 Кб13итог3.pdf
#
29.03.20151.5 Mб48итог4.doc
#
29.03.2015751.1 Кб10итог5.doc
#
29.03.20151.05 Mб18итог6.doc
#
01.05.2025134.3 Кб0Итоговая контрольная работа.docx
#
29.03.201513.38 Кб18Итоговое задание по предмету Социологии.docx