46. Распределение молекул газа по скоростям. Распределение Максвелла.

Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v₁ и v₂ . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от до, отдои отдо, определяются функцией распределения Максвелла

где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, чтсг число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид

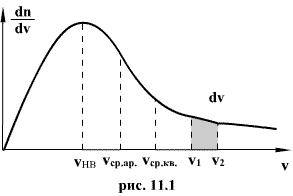Распределение Максвелла достигает максимума при скорости , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.

Кривая распределения Максвелла позволит найти среднюю арифметическую скорость

.Таким образом,

С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.

47. Барометрическая формула. Распределение Больцмана.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуруT и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного паденияg одинаково), барометрическая формула имеет следующий вид:

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), M — молярная массагаза,R — газовая постоянная,T — абсолютная температура. Из барометрической формулы следует, что концентрация молекулn (или плотность газа) убывает с высотой по тому же закону:

где m — масса молекулы газа, k — постоянная Больцмана.

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с закономраспределения Больцмана:

n = n₀exp( -mgh / kT )

где n - концентрация молекул на высоте h, n₀ - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

Мы можем видеть, что концентрация молекул у дна сосуда оказывается выше, чем концентрация в верхней части сосуда. Под действием теплового движения молекулы подбрасываются вверх, а затем падают вниз за счет действия сил тяжести.

Если высота сосуда много меньше чем kT/mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. Принимая во внимание, что P = nkT, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты:

P = P₀exp( -mgh / kT )

Измеряя давление за бортом самолёта, мы можем вычислить при помощи барометрической формулы приблизительную высоту полёта.