1 .Кинематика материальной точки. Системы отсчета. Траектория, перемещение, путь, средняя путевая и средняя скорость по перемещению. Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Основная задача механики – определить положение тела в любой момент времени.

Механическое движение – это изменение положения тела в пространстве с течением времени относительно других тел. Материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь.

Система отсчета – тело отсчета, система координат, связанная с ним, и прибор для измерения времени.

Перемещение – направленный отрезок (вектор) между начальным и конечным положением тела.

Траектория (l) – линия, вдоль которой движется тело. Путь (S) – длина траектории. Скорость (V) – величина, показывающая какой путь проходит тело за единицу времени.

Скорость движения

Средняя путевая скорость

Мгновенная скорость/ скорость движения

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за одну секунду перемещается на один метр.

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

При движении материальной точки М ее координаты и радиус-векторизменяются с течением времени t.

Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:

(1.2)

либо зависимость от времени радиус-вектора этой точки

(1.3)

Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки.

2. Мгновенная скорость. Путь, как интеграл. mгновенная скорость или скорость в данный момент времени. Если в выражении перейти к пределу, устремляяк нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.

(1.6)

В процессе уменьшения величины точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектори скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можно разложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.

(1.7)

где - проекции вектора скорости на оси координат х, у, z.

Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:

(1.8)

Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:

(1.9)

Поэтому численное значение скорости:

(1.10)

Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.

Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.

3. Равномерное и равнопеременное движения. Координатное и графическое представления.

Равномерное прямолинейное движение

Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения.

Вектор скорости равномерного прямолинейного движения материальной точки направлен вдоль ее траектории в сторону движения. Вектор скорости при равномерном прямолинейном движении равен вектору перемещения за любой промежуток времени, поделенному на этот промежуток времени:

Примем линию, по которой движется материальная точка, за ось координат ОХ, причем за положительное направление оси выберем направление движения точки. Тогда, спроецировав векторы r и v, на эту ось, для проекций ∆rx = |∆r| и ∆vx = |∆v| этих векторов мы можем записать:

, отсюда получаем уравнение равномерного движения:

Т.к. при равномерном прямолинейном движении S = |∆r|, можем записать: Sx = Vx · t. Тогда для координаты тела в любой момент времени имеем:

где - координата тела в начальный момент t = 0.

Равнопеременное прямолинейное движение

Равнопеременным называется движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково, т.е. на равные величины. Это движение может быть равноускоренным и равнозамедленным.

Если направление ускорения а совпадает с направлением скорости V точки, движение называется равноускоренным. Если направление векторов а и V противоположны, движение называется равнозамедленным.

При равнопеременном прямолинейном движении ускорение остается постоянным и по модулю и по направлению (а = const). При этом среднее ускорение а_ср равно мгновенному ускорению а вдоль траектории точки. Нормальное ускорение при этом отсутствует (а_n=0).

Изменение скорости ∆v = v - v₀ в течении промежутка времени ∆t = t - t₀ при равнопеременном прямолинейном движении равно: ∆v = a·∆t, или v - v₀ = a·(t - t₀). Если в момент начала отсчета времени (t₀) скорость точки равна v₀ (начальная скорость) и ускорение а известно, то скорость v в произвольный момент времени t: v = v₀ + a·t. Проекция вектора скорости на ось ОХ связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением: v_х = v_0х ± a_х·t. Аналогично записываются уравнения для проекций вектора скорости на другие координатные оси.

Вектор перемещения ∆r точки за промежуток времени ∆t = t - t₀ при равнопеременном прямолинейном движении с начальной скоростью v₀ и ускорением а равен:

а его проекция на ось ОХ (или перемещение точки вдоль соответствующей оси координат) при t₀ = 0 равна:

Путь S_x, пройденный точкой за промежуток времени ∆t = t - t₀ в равнопеременном прямолинейном движении с начальной скоростью v₀ и ускорением а, при t₀ = 0 равен:

Так как координата тела равна х = х₀ + S, то уравнение движения тела имеет вид:

Возможно так же при решении задач использовать формулу:

4. Криволинейное движение. Нормальное и тангенциальное ускорение.

Криволинейное движение – это движения, траектории которых представляют собой не прямые, а кривые линии. (движение всегда с ускорением)

Частный случай – движение по окружности.

При криволинейном движении ускорение представляем, как сумму нормального и тангенциального ускорения.

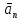- нормальное ускорение, направлено к центру кривизны траектории и характеризует изменения скорости по направлению:

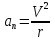
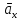- тангенциальное ускорение направлено по касательной к траектории и характеризует изменения скорости по модулю.