17.ФНП

z= f(x,y) – функция 2 пременых

Где х,у – аргументы (независ. Переменые)- z функция(завис. Перемен)

Также z= f(x,y) можно рассмотреть как функцию т. М(х.у) на плоскости Оху

Также М(х0.у0,z0) где z0= f(x0,y0) апликата в системе координат Охуz

18.Предел фнп

число А предел z= f(x,y) при х->x0, y->y0

19.Повторный предел

и пределы наоборот

Рассмотрим функцию двух переменных , определенную в некоторой выколотой окрестности точки. Выберем и зафиксируем переменную. Получим функцию как бы одной переменной. Рассмотрим предел:

Будем считать, что существует. Теперь снимем фиксацию с переменнойи рассмотрим следующий предел:

Если этот предел существует, то говорят, что есть повторный предел функциив точке.

Аналогично мы можем фиксировать сначала переменную . В этом случае мы также получим повторный предел, но, вообще говоря, другой:

Это определение можно распространить и на функции нескольких переменных .

20.Непрерывность ФункцийНесколькихПеременных

z= f(x,y) назнепр в т М0, если:

1. Определена в т М0 или её окрестности

2. Имеет предел

3. 

21.Равномерная непрерывность числовых функций

Основная статья: Непрерывная функция

Числовая функция вещественного переменного равномерно непрерывна, если

Здесь важно, что выбор зависит только от величины .

Равномерная непрерывность отображений метрических пространств

Пусть даны два метрических пространства и 

Отображение называется равноме́рнонепреры́вным на подмножестве если

22.частная производная. Полное приращение ФНП

z= f(x,y) пусть у неизмена а ∆х приращение х

тогда ∆_хz= f(x+∆х,y) - f(x,y) частное приращение z по х( также по у)

полное приращение ∆z= f(x+∆х,y+∆у)- f(x,y)

если существует предел для частного приращения по х

- это и есть частная производная z по х

Также для у

23.производная сложной функции

Пустьz= f(x,y) где y=y(t) a x=x(t) =>z= f(x(t),y(t))

Теорема. Если z= f(x,y) дифиринциуема в т.М(х,у), а y=y(t) и x=x(t) диференциуемы по t то сложная производная вычесляетьсяпо формуле

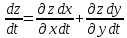
Док-во:дадим t приращение∆t, следавательнох,у получат приращение ∆х, ∆у а z -∆z

Т.к. z= f(x,y) дифиринциуема в т.М(х,у) то

Где перейдем к пределу по ∆t ->0

=>

24.полный деференциал

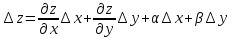
гдеглавная часть приращения функции

для независимых переменных х,уа=>

При

25.Производные высших порядков

- производные 1 порядка

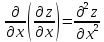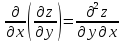, ,производные 2 порядка,

Также и производные высшего порядка например 3:

№241. Полный d

Пусть полное приращение функции Δf(x,y,z) функции f(x,y,z) можно разложить на сумму двух членов:

Δf(x,y,z) = (AΔx + BΔy + CΔz) + ε,

где коэффициенты A, B и C не зависят от Δx,Δy,Δz, а ε = ε(Δx,Δy,Δz) и имеет высший порядок относительно расстояния .

Тогда первый член

AΔx + BΔy + CΔz

называется полным дифференциалом функции f(x,y,z) и обозначается df(x,y,z).

2. Инвариантность ( Примеру удалить!!!!!!!!!!!)

Инвариантность формы первого дифференциала

Дифференциал функции в точкеимеет вид:где— дифференциал тождественного отображения:

Пусть теперь Тогда, и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

[править]Пример

Пусть Тогда функцияможет быть записана в виде композициигде

Дифференцируя эти функции отдельно:

получаем

№26Дифференциал высшего порядка функции одной переменной

Для функции, зависящей от одной переменной   второй и третий дифференциалы выглядят так:

Отсюда можно вывести общий вид дифференциала n-го порядка от функции  :

При вычислении дифференциалов высших порядков очень важно, что  есть произвольное и не зависящее от  , которое при дифференцировании по   следует рассматривать как постоянный множитель.