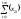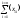Составление матриц значений.

Матрица 1

Матрица 2

Матрица 3

Матрица 4

n

n

n

Для расчета определителей матрицы воспользуемся встроенной функцией Excel "мопред", где в качестве массива укажем соответствующие ячейки в каждой матрице (для вычисления значений определителей необходимо указывать ячейки расположенные в верхнем левом и нижнем правом углах матрицы).

Обозначим в нашем примере "D" – определитель матрицы. Тогда:

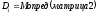
Тогда значения коэффициентов "а" будут определены по формулам:

(6)

(7)

(8)

Определив значения "а" мы можем провести расчет значений по формуле (2) для значений x_1i и x_2i известных за исследуемый период. Если наш расчет верен, то сумма

Расчет статистической значимости уравнения регрессии.

Расчет статистической значимости уравнения регрессии проводим на основании критерия Фишера:

(9) где:

- полная вариация зависимой переменной (продажи), обусловленная вариацией независимых переменных (реклама и продавцы);

(10) где:

- вариация зависимой переменной (продажи), обусловленная вариацией неизвестных факторов, не включенных в настоящее исследование

(11)

Для расчета вариации регрессии и остаточной вариации к табл. 1 добавляем два столбца, соответственно, рассчитываем значения и , вычисляем значения выражений 10 и 11.

Если мы провели расчеты правильно, то у нас должно получиться равенство:

(12) где:

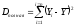(13)

- число степеней свободы числителя;

(14) где:

k - количество независимых переменных, в нашем примере k=2;

- число степеней свободы знаменателя;

(15)

Найденное значение критерия Фишера F необходимо сравнить с табличным значением. Если то связь между зависимой переменной (продажи) и независимыми переменными (реклама, продавцы) есть и является линейной статистически значимой, т.е. мы можем проводить исследование на предмет выяснения влияние каждой независимой переменной (реклама, продавцы) на зависимую переменную (продажи). В противном случае, если 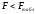связь между изучаемыми явлениями не является статистически значимой и необходимо либо определять другие независимые переменные, которые оказывают влияние на изучаемую величину (продажи), либо связь является нелинейной и необходимо исследовать другую форму взаимосвязи.

Расчет статистической значимости коэффициентов регрессии

Расчет статистической значимости коэффициентов регрессии проводим на основании критерия Стьюдента.

Расчет статистической значимости коэффициента а₁

(16) где:

- стандартная ошибка коэффициента уравнения регрессии;

(17) где:

- см. (11)

Величину 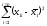находим при помощи встроенной функции Excel "Квадроткл (х11:х112)"

- средняя величина расходов на рекламу за 12 месяцев;

Расчет статистической значимости коэффициента а₂

(18) где:

- стандартная ошибка коэффициента уравнения регрессии;

(19) где:

- см. (11)

Величину находим при помощи встроенной функции Excel "Квадроткл (х11:х112)"

- средняя величина количества продавцов за 12 месяцев;