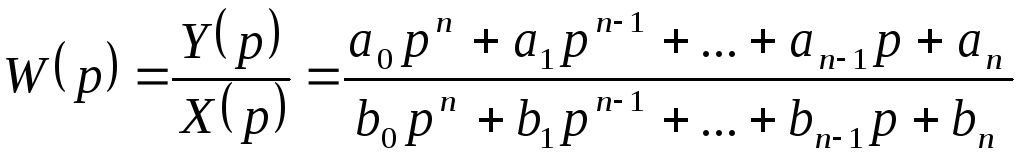7 Математическое описание элементов и систем управления

Для проведения теоретических исследований САР и её отдельных элементов необхо­димо иметь уравнения, описывающие их поведение при изменяющих­ся внешних воздействиях. Эти уравнения представляют собой выраженные в математической форме соотношения, связывающие входные и выходные сигналы и воздействия.

С целью упрощения получения математических соотношений обычно вводят следующие допущения:

- САР и ее элементы обладают свойством стационарности;

- элементы САР являются линейными;

• протекающие процессы являются непрерывными функциями времени при выполнении нулевых начальных условий.

В обобщенном виде САР представлена на рис. 2.1.

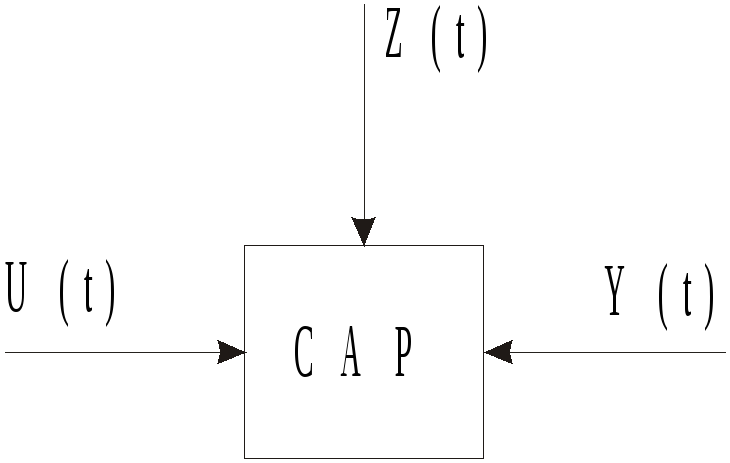
В общем случае действие непрерывной линейной САР описывается неоднородным дифференциальным уравнением следующего вида:

(2.1)

где a, b, c - постоянные коэффициенты, зависящие от параметров системы.

Введем оператор дифференцирования. Тогда уравнение (2.1) может быть представлено в операторном виде:

(2.2)

В выражении (2.2) полином, стоящий при выходном параметре Y, называется собственным оператором и обозначается Q(p). Полиномы при воздействиях Х и Z называются соответственно операто­ром управляющего воздействия и оператором возмущающего воздействия. Оператор управляющего воздействия обозначим R₁(p), а оператор возмущающего воздействия обозначим R₂(p). С учётом введенных обозначений уравнение (2.2) примет вид:

(2.3)

Если рассматривается только установившейся режим, то уравнение (2.2) примет вид:

(2.4)

Таким образом, уравнение (2.2) описывает как динамику, так и статику САР, а уравнение (2.4) описывает только статику.

В тех случаях, когда система или её составной элемент описывается дифференциальным уравнением не выше 2-го порядка, применяется стандартная форма записи уравнения.

Например, имеем САР, содержащую один вход X и один выход Y, которая описывается уравнением:

(2.5)

Левую и правую часть уравнения (2.5) разделим на коэффициентa₂:

(2.6)

Введем обозначения

Тогда уравнение (2.6) примет вид:

(2.7)

В уравнении (2.7) параметр Т₁ имеет размерность сек^-2, параметр Т₂ –сек^-1, а параметр К является безразмерным. Выражение (2.7) представляет собой уравнение в стандартной фор­ме, которая является наиболее удобной при дальнейшем анализе динамических процессов. В этом случае собственный оператор Q(p) принимает вид алгебраического уравнения:

8 Статические характеристики

9.Прямое преобразование Лапласа

Это отношение прямого преобразования Лапласа сигнала на выходе звена к прямому преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Допустим динамика описывается дифференциальным управлением:

Применим к данному уравнению прямое преобразование Лапласа: