
Тест - Планиметрия
.doc-
В прямоугольнике диагонали пересекаются под углом в 600, а сумма диагонали и меньшей стороны равна 36. Диагональ равна
-
В выпуклом четырехугольнике два угла относятся как 3: 5, третий равен их разности, а четвертый больше третьего на 120. Меньший угол равен
-
Вертикальный шест высоты 2 м дает тень в 1,2 м. Высота столба, тень от которого составляет 4,5 м, равна
-
В прямоугольной трапеции основания равны 4 и 8, а меньшая диагональ -
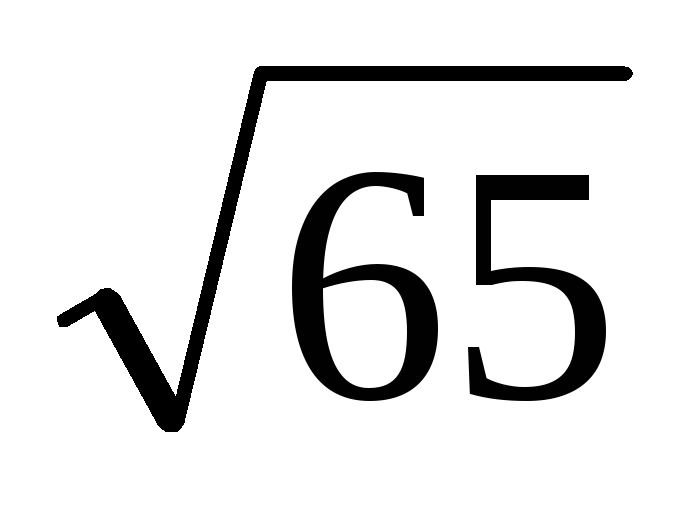 .
Площадь трапеции составляет
.
Площадь трапеции составляет -
Стороны четырехугольника относятся как 2:4:3:6. Периметр подобного ему четырехугольника составляет 150. Меньшая из сторон второго четырехугольника равна
-
В параллелограмме, периметр которого равен 84, а высоты относятся как 3:4, меньшая сторона составляет
-
В трапеции с высотой h боковые стороны и меньшее основание равны половине большего основания. Площадь трапеции равна
-
Площадь параллелограмма со сторонами 5 и 6 составляет
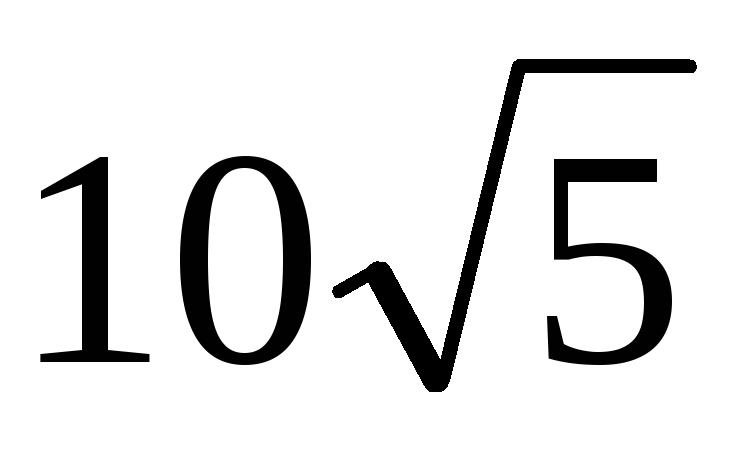 .
Большая диагональ параллелограмма
равна
.
Большая диагональ параллелограмма
равна -
Стороны прямоугольника, вписанного в окружность радиуса R, относятся как a:b. Площадь прямоугольника равна
-
В равнобедренном треугольнике радиус вписанного круга составляет 0,2 его высоты, а периметр треугольника равен 60. Меньшая сторона треугольника равна
-
Площади вписанного и описанного около окружности правильных шестиугольников относятся как
-
К окружности радиуса 5 из точки А проведена касательная длины
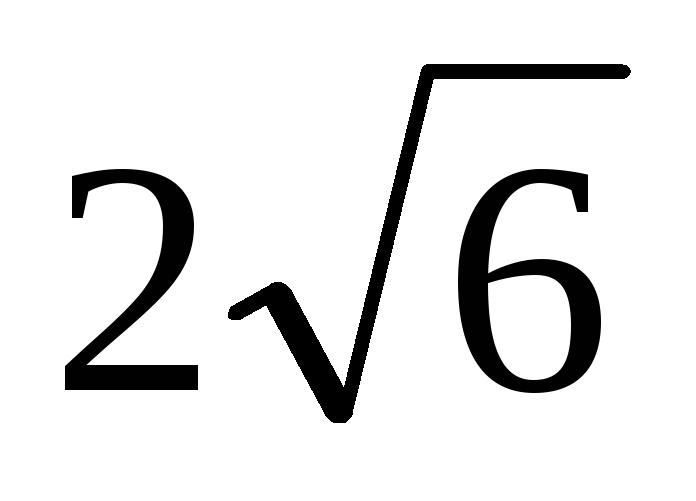 .
Расстояние от точки А до ближайшей
точки окружности равно
.
Расстояние от точки А до ближайшей
точки окружности равно
-
В треугольнике основание равно 60, а высота и медиана, проведённые к нему – 12 и 13. Большая боковая сторона равна
-
В окружность вписаны квадрат и прямоугольник с углом между диагоналями. Отношение их площадей равно
-
В равнобедренной трапеции, описанной около окружности, основания равны 20 см и 5 см. Радиус окружности составляет
-
Высота, проведённая из вершины прямого угла треугольника, делит угол в отношении 1:2. Площадь треугольника она делит в отношении
-
Окружности радиусов 2 и 3 касаются внутренним образом. Наибольшая из хорд большей окружности, касающихся меньшей, имеет длину
-
Правильный треугольник вписан в единичный квадрат так, что они имеют одну общую вершину. Площадь треугольника равна
-
В трапеции боковые стороны равны меньшему основанию, а диагонали - большему. Острый угол трапеции составляет
-
Основания равнобочной трапеции относятся как 2:5, а диагональ делит острый угол пополам. Тангенс этого угла равен
-
В прямоугольном треугольнике катеты составляют 10 и 24. Радиус вписанной в треугольник окружности равен
-
Две окружности касаются друг друга и сторон прямого угла. Отношение их радиусов равно
-
Высота трапеции с основаниями 10 и 30 и сторонами 13 и
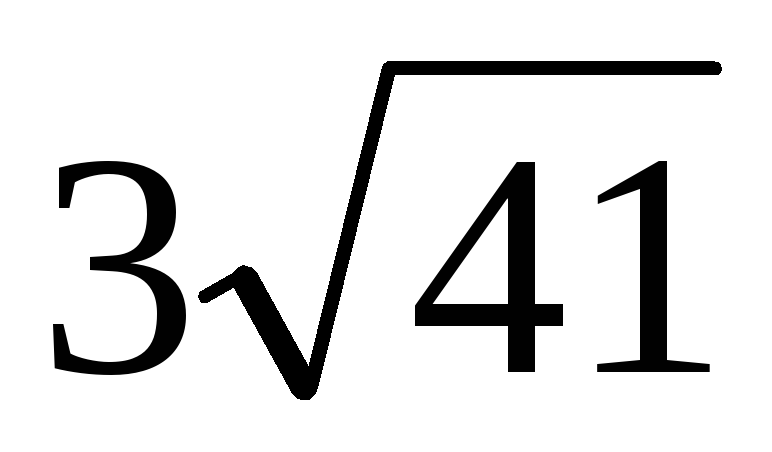 равна
равна -
В круге расстояние между параллельными хордами длины 10 и 24 равно 17. Площадь круга равна
-
Площадь трапеции с высотой 12 и диагоналями 20 и 15 равна
-
В окружности радиуса 1, хорда, стягивающая некоторую дугу, равна
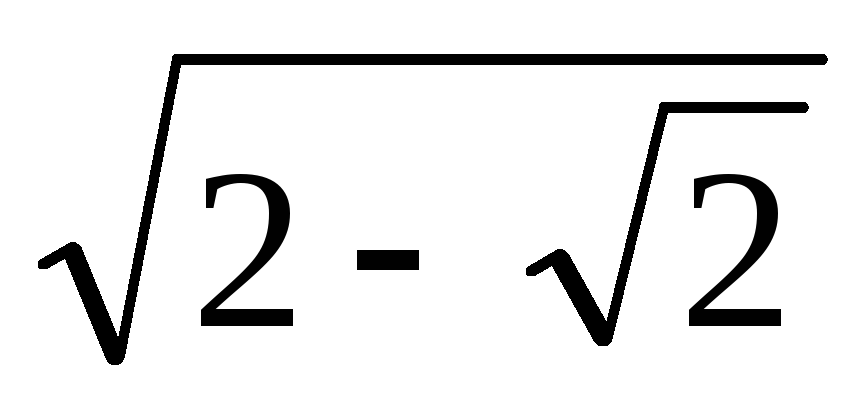 .
Хорда, стягивающая вдвое большую дугу,
равна
.
Хорда, стягивающая вдвое большую дугу,
равна -
Окружность, вписанная в ромб, точкой касания делит его сторону в отношении 2:3. Синус угла ромба равен
-
Последовательность квадратов, начиная с единичного, такова, что вершины последующего делят стороны предыдущего в отношении 3:1. Сумма площадей всех членов этой последовательности равна
-
Равнобедренная трапеция с острым углом описана около окружности. Точка касания окружности делит боковую сторону, считая от меньшего основания, в отношении
-
В описанной около круга неравнобочной трапеции диаметр, перпендикулярный основаниям, делит площадь трапеции в отношении 1:2. Отношение синусов острых углов трапеции равно
