9.3. Определение перемещений
Прогиб стержня при косом изгибе определяется на основании принципа суперпозиции как геометрическая сумма прогибов от независимого действия прямых поперечных изгибов в направлении главных осей инерции сечения. При этом искомый полный прогиб
где u и v – соответственно составляющие по осям х и у, вычисленные любым известным методом.
Например, перемещение концевого сечения консольной балки (рис. 9.5), нагруженной силой F, будет равно
,
где
и
– перемещение концевого сечения
консольной балки в направлении
соответствующих осейх
и у,
определяемые, например, по способу
Верещагина; Fх
= Fcos
,
Fy
= Fsin
.
Покажем, что в каждом сечении балки полный прогиб перпендикулярен нейтральной линии:
,
.
(9.10)
Здесь – угол наклона полного прогиба к оси x.
Произведение угловых коэффициентов полного прогиба и нейтральной оси будет равно
.
Пример
На двухопорную балку с консолью действует распределенная нагрузка q = 20 кН/м в вертикальной плоскости и сила F = 20 кН в горизонтальной плоскости l = 4 м, а = 1 м, [] = 160 МПа, Е = 2105 МПа.
Подобрать сечение
двутавра и прямоугольника с отношением
сторон
.
Оценить отношение весов балок двутаврового
и прямоугольного сечения. Построить
эпюру напряжений, найти положение
нейтральной линии, определить перемещение
сеченияС
для балки
прямоугольного сечения.
Решение
1. Определение реакций на опорах от сил, действующих в вертикальной и горизонтальной плоскостях.
,
Проверка
2. Анализ внутренних силовых факторов от сил, действующих в вертикальной и горизонтальной плоскостях, построение эпюр Q и М.
Вертикальная плоскость
,
Горизонтальная плоскость
Строим эпюры поперечных сил и изгибающих моментов от сил, действующих в вертикальной плоскости (рис. 9.6, а, б) и от сил, действующих в горизонтальной плоскости (рис. 9.6, в, г).
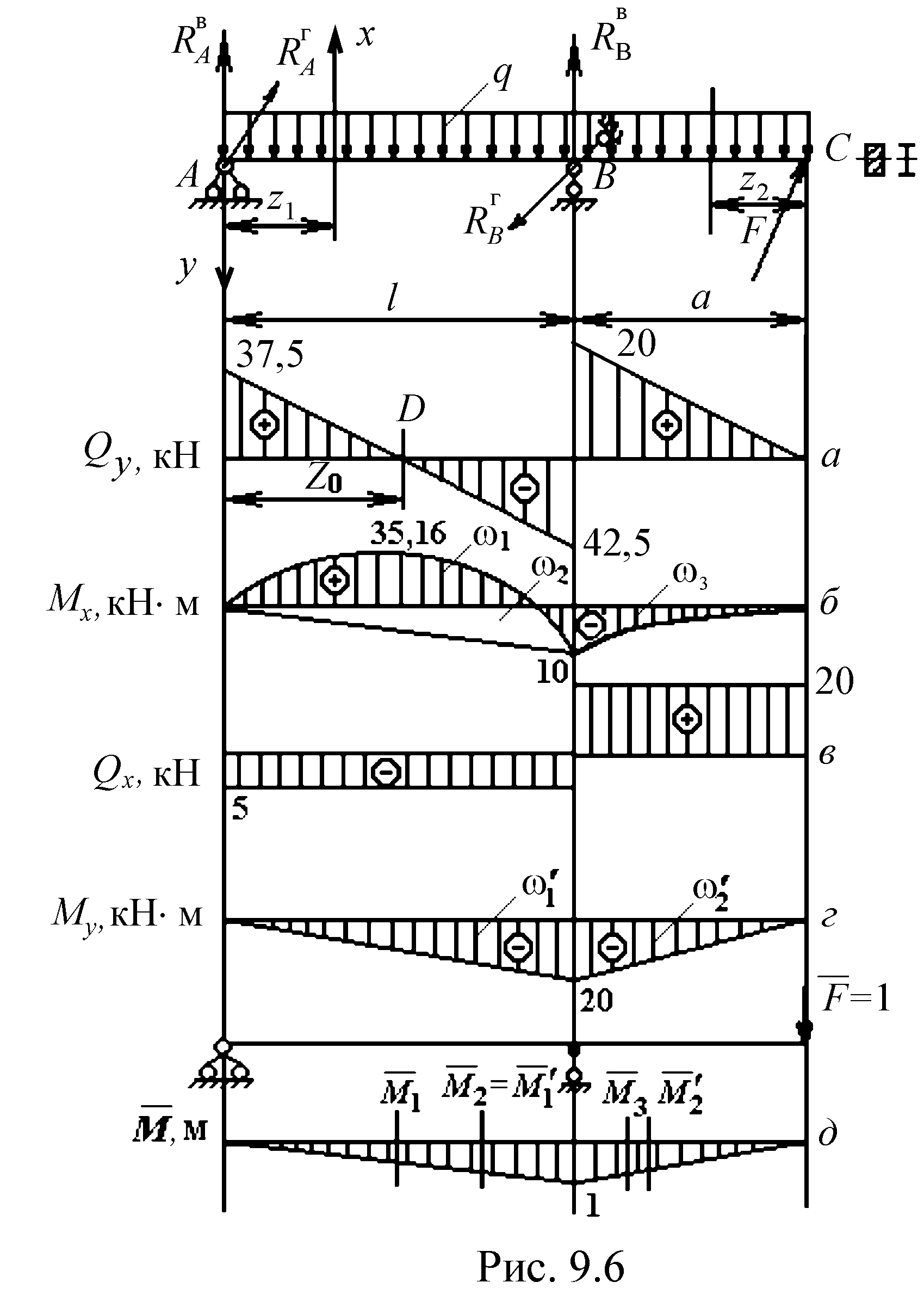
Определяем экстремальное значение изгибающего момента в пролете от сил, действующих в вертикальной плоскости.
3. Определение экстремального значения расчетного момента.
На основании формулы (9.8) расчетный изгибающий момент на первом участке для прямоугольного сечения при K = 2 равен
,
.
Экстремальное значение расчетного момента
.
Расчетный изгибающий момент в сечении В:
.
Наибольший расчетный
момент имеем в пролете:
.
Для двутаврового сечения приK = 8
определяем расчетный момент в пролете:
На опоре В
Опасным
сечением для двутавра будет сечение В
с
4.
Подбор сечений из условия прочности
:
а) прямоугольное сечение:
тогда
принимаем
б) двутавровое сечение:
1-е приближение:
№ 45,
2-е приближение:
№ 50,
Перенапряжение составляет
3-е приближение:
№ 55,
Недонапряжение составляет
Принимаем двутавр № 50.
Определим отношение площадей прямоугольного сечения и двутавра.
Из найденного отношения следует, что значительная рациональность двутавровых сечений по отношению к прямоугольным, полученная при плоском поперечном изгибе, ощутимо снижается при косом изгибе.
6. Определим рациональное положение балок.
Повернем сечения балок на 90.
Для прямоугольника
,
(в пролете).
(в сечении В).
Положение сечения на рис. 9.7 не рациональное, так как напряжения значительно возросли.
Двутавровое сечение:
,
(в пролете).
(в сечении В).
Положение двутавра на рис. 9.7 не рациональное.
7. Построение эпюры нормальных напряжений в аксонометрии для прямоугольного сечения в опасном сечении.
Опасное сечение находится на расстоянии 2,375 м от опоры А. Определим изгибающие моменты Мх и Му в этом сечении.
,
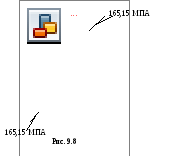
8. Определение положений силовой и нейтральной линий.
Положение силовой линии:
Положение нейтральной линии:
Силовая и нейтральная линии изображены на рис. 9.8.
9. Определение полного перемещения сечения С.
Определим перемещение способом Верещагина в плоскости yAz и xAz для балки двутаврового сечения.
Эпюра вспомогательного состояния от единичной силы изображена на рис. 9.6, д.
Полное перемещение сечения С.
