
- •Текст каждого задания вместе с номером варианта и исходными данными приводят в контрольной работе на отдельной странице.
- •1. Нестационарная теплопроводность Варианты заданий
- •Задание
- •Содержание отчета
- •2. Конвективный теплообмен и тепловое излучение Варианты заданий
- •Задание
- •Содержание отчета
- •1. Указания к выполнению задания по теме «нестационарная теплопроводность»
- •1.1.Аналитическое решение нестационарных задач теплопроводности
- •1.1.1. Охлаждение неограниченной пластины ()
- •1.2. Регулярный режим охлаждения
- •2.1. Теплообмен в жидкостях и газах.
- •2.2. Тепловое излучение.
Задание
Определить число Nu, коэффициент теплоотдачи
 и плотность теплового потока: при
свободной конвекции в воде и воздухе;
при вынужденной конвекции в воде и
воздухе; и плотность теплового потока
за счет теплового излучения тела.
и плотность теплового потока: при
свободной конвекции в воде и воздухе;
при вынужденной конвекции в воде и
воздухе; и плотность теплового потока
за счет теплового излучения тела.Для тела, помещенного в воздушную среду построить зависимость плотности теплового потока от температуры при свободной конвекции, вынужденной конвекции и тепловом излучении. Нижняя граница температурного интервала определяется по величине
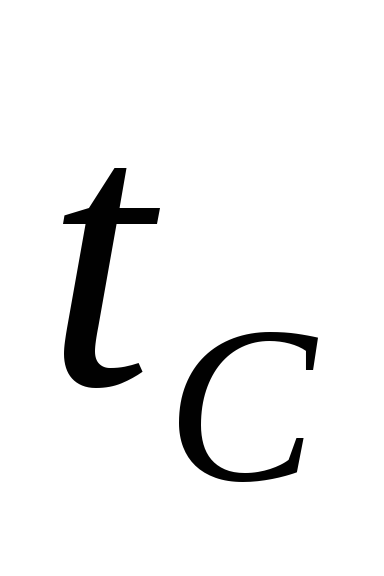 ,
указанной в таблице задания, верхняя
граница определяется по результату
,
указанной в таблице задания, верхняя
граница определяется по результату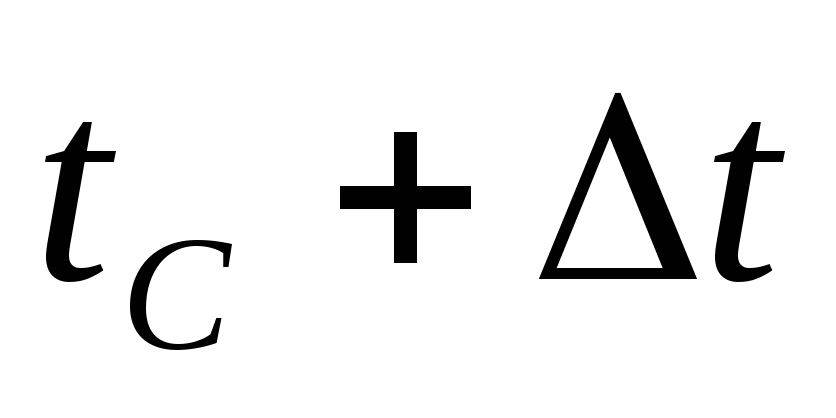 .
Все три кривые поострить на одних осях.
.
Все три кривые поострить на одних осях.Построить изменение коэффициента теплоотдачи
 от скорости потока воздуха и воды.
Нижняя граница скоростного интервала
определяется по величине
от скорости потока воздуха и воды.
Нижняя граница скоростного интервала
определяется по величине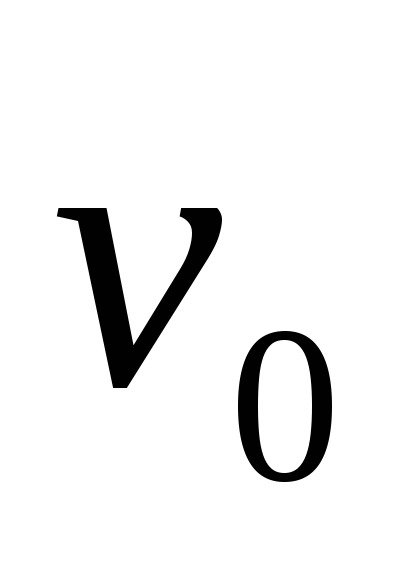 ,
указанной в таблице задания, верхняя
граница определяется по результату
,
указанной в таблице задания, верхняя
граница определяется по результату .
.Построить изменение коэффициента теплоотдачи
 от изменения угла атаки потока воды и
воздуха. Нижняя граница скоростного
интервала определяется по результату
от изменения угла атаки потока воды и
воздуха. Нижняя граница скоростного
интервала определяется по результату ,
верхняя граница равна
,
верхняя граница равна .
.
Содержание отчета
1. Задание.
2. Привести расчетные формулы с подстановкой данных и результаты вычислений.
3. Построить все зависимости указанные в задании и результаты по каждой зависимости свести в таблицы.
4. Выводы по работе.
1. Указания к выполнению задания по теме «нестационарная теплопроводность»
Описание процесса теплопроводности включает в себя дифференциальное уравнение и условие однозначности.
Дифференциальное уравнение теплопроводности имеет вид:
![]() , (1.1)
, (1.1)
где
t– температура,С;- время, с;![]() – коэффициент температуропроводности,
м2/с;-
коэффициент теплопроводности, Вт/(мС);
с - удельная теплоемкость, Дж/(кгС);- плотность вещества,
кг/м3;qv
– мощность внутреннего источника
теплоты, Вт/м3.
– коэффициент температуропроводности,
м2/с;-
коэффициент теплопроводности, Вт/(мС);
с - удельная теплоемкость, Дж/(кгС);- плотность вещества,
кг/м3;qv
– мощность внутреннего источника
теплоты, Вт/м3.
Условия однозначности включают в себя: физические условия; геометрические условия; начальные условия; граничные условия.
Дифференциальное уравнение теплопроводности с условиями однозначности дают законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании температурного поля тела в любой момент времени.
1.1.Аналитическое решение нестационарных задач теплопроводности
1.1.1. Охлаждение неограниченной пластины ()
Постановка задачи: Дана пластина толщиной
2δ. Если толщина пластины мала по сравнению
с длиной и шириной, то такую пластину
обычно считают неограниченной. При
заданных граничных условиях коэффициент
теплоотдачи α одинаков для всех точек
поверхности пластины. Изменение
температуры происходит только в одном
направлении Х, в двух других направлениях
температура не изменяется
![]() ,
следовательно, в пространстве задача
является одномерной.
,
следовательно, в пространстве задача
является одномерной.
Начальное
распределение температуры задано:
t(x,0)=t0.
Охлаждение происходит в среде с постоянной
температуройtж=const.
На обеих поверхностях отвод тепла
осуществляется при постоянном во
времени коэффициенте теплоотдачи.
Отсчет температуры пластины для любого
момента времени будем вести от температуры
окружающей среды, т.е.
![]() .
Так как задача в пространстве одномерная,
то дифференциальное уравнение примет
вид:
.
Так как задача в пространстве одномерная,
то дифференциальное уравнение примет
вид:
![]() .
(1.2)
.
(1.2)
Начальные условия: при τ = 0 υ = υо.
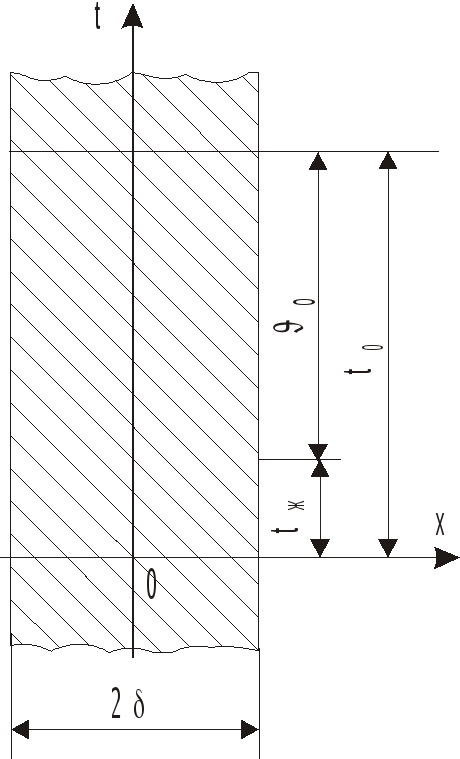
Рис. 1.1. К охлаждению плоской неограниченной пластины
При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины, как показано на рис. 1.1. При этом граничные условия на оси и на поверхности пластины запишутся так:
на оси пластины х = 0
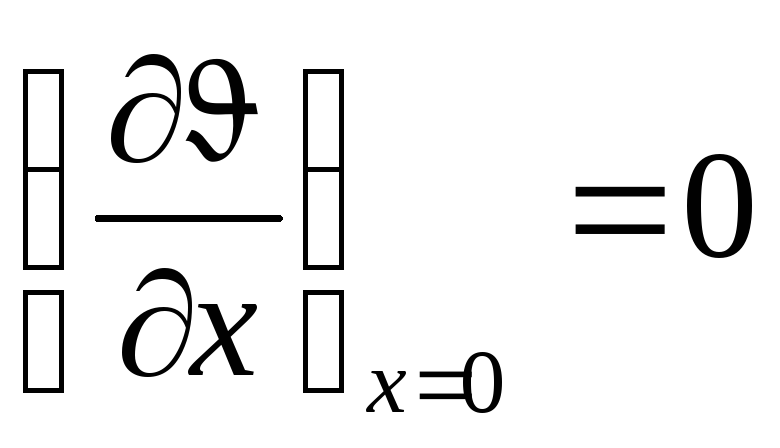 ;
;на поверхности пластины при х = δ
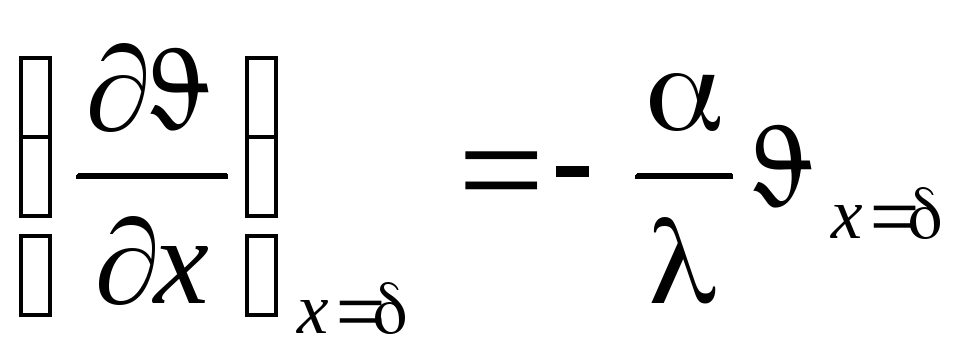 .
.
Дифференциальное уравнение (1.2) совместно с начальными и граничными условиями однозначно формируют поставленную задачу. Решение дифференциального уравнения (1.2) с учетом начальных и граничных условий и даст искомое распределение температуры в плоской пластине.
Решением дифференциального уравнения (1.2) является:
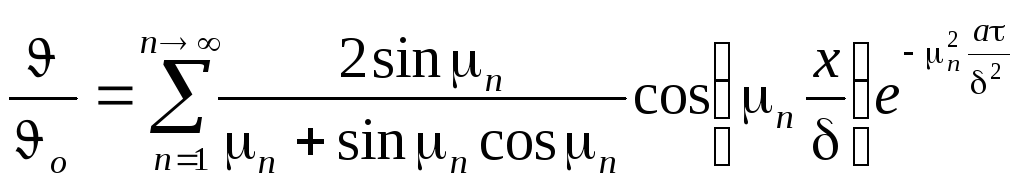 , (1.3)
, (1.3)
где
![]() -
корни характеристического уравнения
-
корни характеристического уравнения
![]() ;
(1.4)
;
(1.4)
![]() - безразмерное
число Био.
- безразмерное
число Био.
Наиболее
просто характеристическое уравнение
(1.4) можно решить графическим методом.
Обозначим левую часть уравнения (1.4)
через
![]() ,
а правую – через
,
а правую – через![]() .
Пересечение котангенсоиды у1
с прямой у2
даст нам значение корней характеристического
уравнения.
.
Пересечение котангенсоиды у1
с прямой у2
даст нам значение корней характеристического
уравнения.
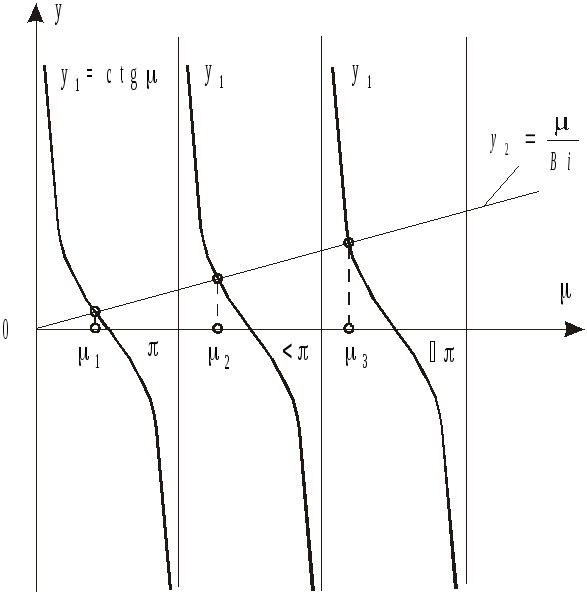
Рис. 1.2. К решению уравнения (1.4)
Из рис. 1.2 следует, что имеется бесконечное множество значений величины μn, причем каждое последующее больше предыдущего:
μ1< μ2< μ3<…< μn<…
1.1.2.
Охлаждение бесконечного цилиндра (![]() )
)
Цилиндр радиусом
rоотдает тепло
окружающей среде через свою боковую
поверхность; коэффициент теплоотдачи
α во всех точках поверхности одинаков
и остается постоянным на протяжении
всего периода охлаждения. Температура
средыtжпостоянна. Начальное распределение
температуры задано:t(r,0)=t0.
Отсчет температуры цилиндра будем
вести, как и в предыдущем разделе, от
температуры окружающей среды![]() .
Требуется найти распределение температуры
внутри цилиндра.
.
Требуется найти распределение температуры
внутри цилиндра.
При этих условиях уравнение теплопроводности принимает вид:
![]() . (1.5)
. (1.5)
Граничные и начальные условия:
при τ = 0 и 0 ≤ r≤ro
![]() ;
;
при τ > 0 и r= 0
![]() ;
;
при τ > 0 и r=rо
![]() .
.
Решением дифференциального уравнения (1.5) является:
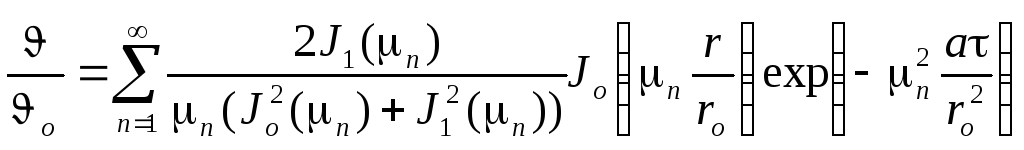 ,
(1.6)
,
(1.6)
где
Jо,
J1
– функции Бесселя первого рода нулевого
и первого порядка;
![]() -
корни характеристического уравнения
-
корни характеристического уравнения
![]() ;
(1.7)
;
(1.7)
![]() - безразмерное
число Био.
- безразмерное
число Био.
Функции Бесселя первого рода n-го порядка (n=0,1,2,..) может вычисляться разложением в ряд:
![]() .
.
При вычислении функции Бесселя число членов ряда задать равным 20.
1.1.3.
Охлаждение шара (![]() )
)
Рассмотрим
охлаждение шара радиусом r0в среде с постоянной температурой и с
постоянным коэффициентом теплоотдачи
α на его поверхности. Температура средыtжпостоянна.
Начальное распределение температуры
задано:t(r,0)=t0.
Отсчет температуры шара будем вести,
как и в предыдущих разделах, от температуры
окружающей среды![]() .
Требуется найти распределение температуры
внутри шара.
.
Требуется найти распределение температуры
внутри шара.
При этих условиях уравнение теплопроводности принимает вид:
![]() . (1.8)
. (1.8)
Граничные и начальные условия:
при τ = 0 и 0 ≤ r≤ro
![]() ;
;
при τ > 0 и r= 0
![]() ;
;
при τ > 0 и r=rо
![]() .
.
Решением дифференциального уравнения (1.8) является:
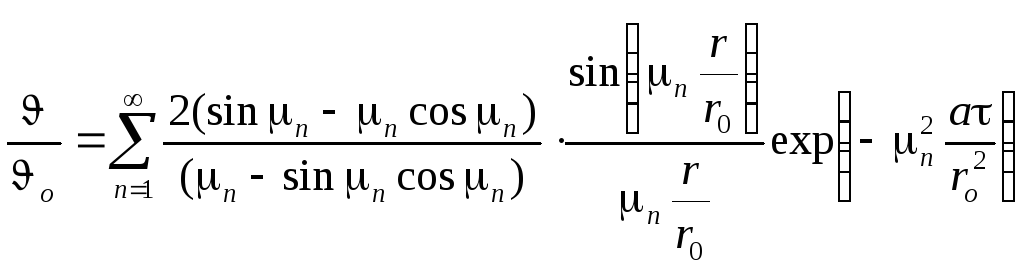 ,
(1.9)
,
(1.9)
где
![]() -
корни характеристического уравнения
-
корни характеристического уравнения
![]() ;
(1.10)
;
(1.10)
![]() - безразмерное
число Био.
- безразмерное
число Био.
